Кривые второго порядка

Пример

Следствие

Для того чтобы квадратичная форма была отрицательно определенной, необходимо и достаточно, чтобы знаки угловых миноров чередовались, причем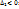

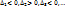
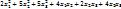
Матрицей квадратичной формы является матрица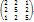

Для нее .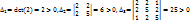

Поэтому данная квадратичная форма – положительно определенная.

8. Прямые и плоскости в точечном пространстве

72. Выведите канонические уравнения прямой в 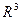, проходящей через данные точк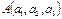и и .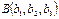

Все точки M(x, y, z) ∈ L определяются из условия, что вектор A−−M→(x−a1, y−a2, z−a3)

должен быть коллинеарен вектору A−→B(b1−a1, b2−a2, b3−a3), что можно задать следующей

системой (условие коллинеарности векторов - пропорциональность координат):

L:x − a1/b1 − a1=y − a2/b2 − a2=z − a3/b3 − a3

73. Выведите уравнение прямой в 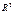, проходящей через данную точку 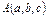в данном направлении .

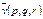Если точка принадлежит l, то вектор 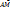коллинеарен . Это записывается с помощью равенств

[1]

Уравнения [1] называются каноническими уравнениями прямой l. В действительности уравнения [1] представляют собой систему из двух уравнений

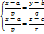
Каждое из которых определяет плоскость (первая из плоскостей параллельна оси z, вторая – оси y).

74. Выведите уравнение плоскости, проходящей через три точк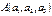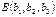и , и ..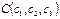

Поскольку речь идет о плоскости, проходящей через точку A и параллельной векторам 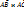, то искомое уравнение будет

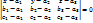
75. Выведите уравнение плоскости в 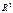, проходящей через данную точку 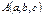, перпендикулярно данному вектору 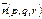. Приведите пример уравнения плоскости в 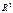, проходящей параллельно какой-либо координатной оси.

Пусть M(x,y,z) – произвольная точка искомой плоскости, тогда необходимо, чтобы вектор AM = (x-a, y-b, z-c) был ортогонален вектору n, то есть их скалярное произведение должно быть равно нулю:

p(x - a) + q(y - b) + c(z - c) = 0

получили уравнение искомой плоскости.

Пример уравнения, проходящего параллельно какой-либо координатной оси:

x=-1. Такая плоскость будет параллельна осям Oy и Oz

76. Две прямые заданы каноническими уравнениям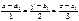и и 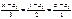. Найдите угол между ними. Ответ обоснуйте.

Угол между плоскостями сводится к углу между нормалями

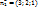
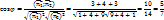
77. Как найти угол между плоскостями в 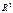по их общим уравнениям 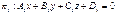, 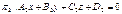? Ответ обоснуйте и приведите пример.

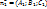
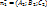
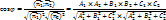
Например: Π1: x + 2 = 0,Π2: x −5 = 0. В этом случае v1(1, 0, 0) и v2(1, 0, 0). Тогда cos(Π1Π2) =

1/√1√1=1, что означает, что плоскости параллельны (что было очевидно).

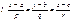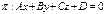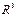78. Как найти угол между прямой и плоскостью в ? Ответ обоснуйте и приведите пример.

Направляющий вектор прямой: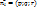

Вектор-нормаль плоскости: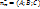

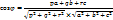
Например: прямая l: x/2 = y/2, z = 0 и плоскость π: y = 2. Очевидно, что угол между прямой и плоскостью равен π/4. Проверим это, использовав полученную формулу. Здесь v(2, 2, 0), w(0, 1, 0)

sin α =2/(√4 + 4√1)=2/2√2=1/√2

Что свидетельствует о том, что угол между прямой и плоскостью равен π/4.

79. Как найти расстояние от точки 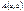до прямой 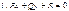? Как найти расстояние между двумя параллельными прямыми в ?

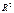80. Как найти расстояние от точки 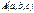до плоскости 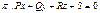? Как найти расстояние между двумя параллельными плоскостями в ?

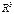Расстояние между двумя параллельными плоскостями можно найти как расстояние между одной из них и точкой, принадлежащей другой плоскости.

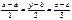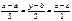81. Запишите общее уравнение плоскости, содержащей прямые и . Ответ обоснуйте.

Назовем прямые L: (х-а)/1=(у-b)/2=(z-c)/3 и М:(x-a)/3=(y-b)/2=(z-c)/1

Полагаем, что точка А (а;b;c) начальная точка, а направляющий вектор для L вектор p(1;2;3) – один из направляющих векторов плоскости π. Направляющий вектор для М вектор q(3;2;1) – второй направляющий вектор плоскости π. Уравнение плоскости π запишем в виде

Откуда, раскрывая определитель, получаем общее уравнение плоскости

Π: -4х+8у-4z +4(a-2b+c)

82. Что представляет собой пересечение двух ортогональных плоскостей в 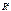? Ответ обоснуйте и приведите пример.

Пересечение любых плоскостей в R3 представляет собой прямую их пересечения. Это

прямая.

83. Запишите общее уравнение линии второго порядка. Какое геометрическое место точек определяется уравнением ?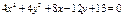

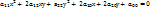
Где коэффициенты 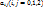– действительные числа, причем 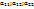не равны нулю одновременно и имеет место симметричность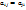

Дата добавления: 2015-03-31