Напишите каноническое уравнение гиперболы. Приведите пример уравнения гиперболы, не пересекающей ось абсцисс. Нарисуйте ее

1)

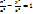
2)

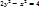
Рассмотрим уравнение гиперболы: x2 − y2 = −1. Ассимптоты данной гиперболы (на-

рисуем их): y = x, y = −x

Построим точку A(0, 1). Нарисуем ветвь вверх, стремящюся на y = ∞ к ассимптотам.

Построим точку B(0,−1). Нарисуем ветвь вниз, стремящюся на y = −∞ к ассимптотам.

90. Являются ли параболами линии, заданные уравнениями: , ? Ответ обоснуйте.

Каноническое уравнение параболы:

y2 = 2px, p > 0

1) y2+2x = 0 - Не является параболой, так как его можно переписать в виде y2 = −2x,где p = −1 < 0, что не удовлетворяет условию p > 0.

В принципе, можно ввести замену координат x’ = −x, тогда в координатах (x’, y) данное уравнение y2 = 2x’ будет задавать параболу.

2) y−2x2 +1 = 0 - Не является параболой, так как y входит в уравнение линейно, что не удовлетворяет условию того, что в каноническом виде параболы переменная y входитс кваратом.

В принципе, можно ввести замену координат y’ = x, x’ = y+1, тогда в координатах (x’, y’)

данное уравнение 2y’2 = x’ будет задавать параболу, если переписать это уравнение в виде:

y’2 = x’/2.

91. Дайте определение кривой второго порядка. Какие кривые второго порядка задают уравнения , 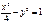? Изобразите их.

Кривой второго порядка называется множество всех точек плоскости, координаты которых удовлетворяют алгебраическому уравнению 2-ой степени.

1) Эллипс. Точки эллипса:

A1(2, 0) A2(0, 3) A3(−2, 0) A4(0,−3)

2)Гипербола.Ее ассимптоты (нарисуем их)

y =x/2, y= −x/2

Построим точку A(2, 0). Нарисуем ветвь вправо, стремящюся на x = ∞ к ассимптотам.

Построим точку B(−2, 0). Нарисуем ветвь влево, стремящюся на x = −∞ к ассимпто-

там.

92. Какая из кривых второго порядка обладает асимптотами? Напишите каноническое уравнение этой линии и уравнения ее асимптот.

Асимптотами обладает только гипербола. Параметры a, b - определяют длины главной (расположенной на оси Ox) и побочной полуоси (расположенной на оси Oy) соответственно. , .

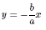10. Выпуклые множества в точечном пространстве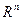

93. Как задать луч, отрезок в точечном пространстве 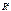? Приведите примеры.

Луч (то есть каждую его точку M(x, y, z)) можно задать с помощью начальной точки

M0(x0, y0, z0), из которой выходит луч и направляющего вектора v(vx, vy, vz) данного луча в виде M = M0 +tv, где t принадлежит R, t больше или равно 0 - параметр уравнения. Расписав полученное уравнение покоординатно, получим систему, задающую все точки луча в параметрическом виде: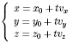

Дата добавления: 2015-03-31