Дайте определение окружности и выведите ее каноническое уравнение

Окружность с центром в точке A(x0, y0) радиуса R > 0 - геометрическое место точек на плоскости, равноудаленных от заданной точки A(x0, y0) на равное заданное расстояние R.

Окружность состоит из точек M(x, y): ρ(M,A) = R, то есть:ρ(M,A) =корень (x − x0)2 + (y − y0)2 = R

Введя замену x' = x − x0, y’ = y − y0 Получим:

Корень x'2 + y’2 = R. Поменяв обозначения и

возведя в квадрат получим каноническое уравнение окружности:x2 + y2 = R2

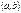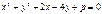85. Напишите уравнение окружности с центром в точке радиуса . При каком значении параметра , уравнение определяет окружность?

1) (x - a + (y - b =

2)

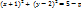
При p > 5 уравнение не задает окружности, так как справа получаем отрицательное

значение, хотя ∀x, y ∈ R слева стоит неотрицательное выражение (сумма квадратов).

При p <= 5 уравнение задает окружность с центром в точке C(−1, 2) радиуса r = √5 − p.

86. Дайте определение эллипса. Запишите его каноническое уравнение. Каков смысл параметров, входящих в каноническое уравнение эллипса? Постройте линию, заданную уравнением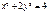

Эллипс – геометрическое место точек на пл-ти, сумма расстояний от каждой из которых до 2 заданных точек F₁ и F₂, называемых фокусами постоянна и равна 2a.

x²/a² + y²/b²=1 = 1 –каноническое уравнение эллипса. 0>E<1.

Факальный параметр p=b²/a, r=p/(1+Ecosφ) – полярное ур-ие.

r₁+r₂=2a – большая ось.

2b – малая ось.

2с – расстояние между фокусами. b² =a²-c².

Е=с/а – эксцентриситет.

x2 + 2y2 = 4

x2/22 + y2/√22 = 1

Главная полуось a = 2. Побочная полуось b = √2. Точки A1(2, 0), A2(0,√2), A3(−2, 0), A4(0,−√2)

- принадлежат эллипсу.

Необходимо нарисовать эллипс, проходящий через указанные точки A1,A2,A3,A4.

87. Как по каноническому уравнению эллипса определить, является ли он окружностью? Ответ обоснуйте.

Рассмотрим каноническое уравнение эллипса:x2/a2 +y2/b2 = 1

Если a = b, то данное уравнение описывает окружность (эллипс становится окружностью).

С точке зрения уравнения, можно домножить на a2, тогда мы получим каноническое уравнение окружности радиуса a: x2 + y2 = a2

С точки зрения геометрии при a = b полуоси эллипса равны, что говорит о его симметрии, то есть эллипс становится окружностью.

При a не= b полуоси у эллипса различные и эллипс не является окружностью.

88. Дайте определение гиперболы. Каков геометрический смысл параметров, входящих в каноническое уравнение гиперболы? Среди линий 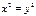, , 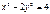выберите гиперболы и постройте их.

Гипербола - геометрическое место точек на плоскости, модуль разности расстояний, от которых до двух заданных точек (фокусы гиперболы) одинаково. Гипербола состоит из точек M(x, y): |ρ(M,F1) − ρ(M,F2)| = 2a = const, где F1, F2 -фокусы гиперболы, a - длина главной полуоси.

Каноническое уравнение гиперболы:

x2/a2 − y2/b2 = 1 основная гипербола

x2/a2 − y2/b2 = −1 сопряженная гипербола

Параметры a, b - определяют длины главной (расположенной на оси Ox) и побочной полуоси (расположенной на оси Oy) соответственно.

1) x2 = y2 - НЕ гипербола. Это уравнение задает пару пересекающихся прямых.

2) x2 − 2y2 = 4 - гипербола: x2/2в2 − y2/√2 = 1, a = 2, b= √2.

3) x2 + 2y2 = 1 - НЕ гипербола: Это уравнение задает эллипс.

Дата добавления: 2015-03-31