Дайте определение выпуклого множества. Докажите, что пересечение выпуклых множеств является выпуклым

Множество X называется выпуклым, если для любых двух его точек A,B ∈ X все точки отрезка [AB] также принадлежат множеству X, то есть если для любых двух его точек A,B ∈ X и для любого значения α in[0; 1] точка M = αA + (1 − α)B также принадлежит множеству X: M ∈ X.

Пусть дано X1,...Xn - выпуклые множества. Обозначим Y =Xi - пересечение выпуклых множеств. Покажем, что Y - выпуклое множество. Для этого покажем, что длялюбых точек A,B ∈ Y и для любого значения α in[0; 1] точка M = αA + (1 − α)B также принадлежит множеству Y: M ∈ Y. Так как Y - суть пересечение выпуклых множеств X1,...Xn, то выбранные произвольным образом точки A,B принадлежат каждому из этих множеств Xi, i = 1..n. В силу выпуклости каждого из множеств Xi по определению следует, что для произвольно выбранного значения α ∈ [0; 1] точка M = αA+(1−α)B принадлежит каждому из множеств (все они выпуклы и содержат A,B). Так как все множества Xi содержат точку M, то и

пересечение этих множеств также содержит точку M: M ∈ Y. Из последнего включения в силу произвольности A,B ∈ Y и произвольности параметра α ∈ [0; 1] следует выпуклость множества Y, что и требовалось показать.

95. Является ли множество точек , удовлетворяющих условию 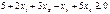, выпуклым? Ответ обоснуйте.

Да, очевидно, что это равенство задаёт линейную полуплоскость в R4.

Обоснуем это по оределению:

Рассмотрим любые две точки этого пространства

A = (a1, a2, a3, a4), B= (b1, b2, b3, b4) ∈ X,

удовлетворяющие вышеуказанному неравенству.

Рассмотрим произвольную точку M = αA + (1 − α)B, где α ∈ [0; 1] – произвольное значение параметра. ТогдаM(m1,m2,m3,m4) = αA + (1 − α)B

m1 = αa1 + (1 − αb1)

m2 = αa2 + (1 − αb2)

m3 = αa3 + (1 − αb3)

m4 = αa4 + (1 − αb4)

Проверим для точки M(m1,m2,m3,m4) принадлежность к множеству X с помощью

выполнимости заданного неравенства:

5 + 2m1 + 3m2 − m3 + 5m4 ≥ 0

5 + 2(αa1 + (1 − αb1)) + 3(αa2 + (1 − αb2)) − (αa3 + (1 − αb3)) + 5(αa4 + (1 − αb4)) ≥ 0

Представим 5 = α5+(1−α)5, раскроем и сгруппируем слагаемые для ai и bi. Получим:

α(5 + 2a1 + 3a2 − a3 + 5a4) + (1 − α)(5 + 2b1 + 3b2 − b3 + 5b4) ≥ 0

Так как точки A,B лежат в множестве X, то их координаты удовлетворяют неравенству,

задающему множество. Значит, оба слагаемых неотрицательны в силу неотрицательности

α и 1 − α. Поэтому последнее неравенство выполнено для любых A,B и любого значения

параметра α ∈ [0; 1]. По определению мы показали, что данное множество X является

выпуклым.

96. Является ли множество точек удовлетворяющих условию 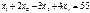, выпуклым? Ответ обоснуйте.

Да, очевидно, что это равенство задаёт линейную гиперплоскость в R4.

Обоснуемэто по оределению:

Рассмотрим любые две точки этого пространства

A = (a1, a2, a3, a4), B= (b1, b2, b3, b4) ∈ X

удовлетворяющие вышеуказанному равенству.

Рассмотрим произвольную точку M = αA + (1 − α)B, где α ∈ [0; 1] – произвольное значение параметра. Тогда M(m1,m2,m3,m4) = αA + (1 − α)B

m1 = αa1 + (1 − αb1)

m2 = αa2 + (1 − αb2)

m3 = αa3 + (1 − αb3)

m4 = αa4 + (1 − αb4)

Проверим для точки M(m1,m2,m3,m4) принадлежность к множеству X с помощью

выполнимости заданного равенства:

m1 + 2m2 − 3m3 + 4m4 = 55

(αa1 + (1 − αb1)) + 2(αa2 + (1 − αb2)) − 3(αa3 + (1 − αb3)) + 4(αa4 + (1 − αb4)) = 55

Раскроем скобки и сгруппируем слагаемые для ai и bi. Получим:

α(a1 + 2a2 − 3a3 + 4a4) + (1 − α)(b1 + 2b2 − 3b3 + 4b4) = 55

Так как точки A,B лежат в множестве X, то их координаты удовлетворяют равенству,

задающему множество, то есть (a1 + 2a2 − 3a3 + 4a4) = 55 и (b1 + 2b2 − 3b3 + 4b4) = 55.

Подставив эти равенства в последнее выражение получим:

α55 + (1 − α)55 = 55

Последнее равенство выполнено для любых A,B и любого значения параметра α ∈ [0; 1]. По определению мы показали, что данное множество X является выпуклым.

97. Приведите примеры выпуклого множества: а) имеющего угловую точку; б) не имеющего угловой точки. Может ли не ограниченное выпуклое множество иметь угловую точку? Приведите пример.

а) квадрат имеет 4 угловые точки

б) окружность не имеет угловых точек

в) неограниченное множество может иметь угловые точки: имеет одну угловую точку (0;0)

98. Дайте определение выпуклой оболочки системы точек. Пусть - выпуклая оболочка точек , , , . Принадлежат ли множеству 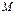точки: 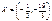, 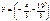? Ответ обоснуйте.

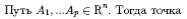
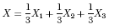то есть выполнено условие того, что это выпуклая линейная комбинация, а значит X входит в состав выпуклой оболочки. Предположим, что Y входит также в выпуклую комбинацию, тогда все точки отрезка [XY ] должны входить в линейную комбинацию, но по исходным точкам видно (все они находятся правей прямой x = -1), что вся выпуклая комбинация расположена справа от прямой x =-1, а точка Y - слева, что подтверждает, что ни весь отрезок [XY ] ни точка Y - не принадлежат выпуклой оболочке.

Дата добавления: 2015-03-31