
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Композиция функций (сложная функция, суперпозиция функций
|
|
|
|
А
Виды функций.
Сужение функции.
Определение. Пусть 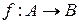 ,
, 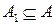 . Сужением функции
. Сужением функции 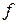 на множество
на множество 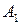 называется
называется 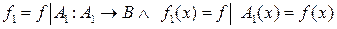 .
.
Пример. 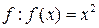 ;
; 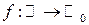 ;
; 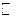 - область определения функции, отмечается точками оси абсцисс.
- область определения функции, отмечается точками оси абсцисс. 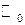 - множество значений функции, отмечается точками оси ординат.
- множество значений функции, отмечается точками оси ординат.
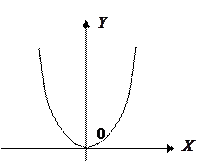 | |||
Рассмотрим сужения этой функции.
а)  ;
; 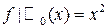 для
для 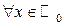 .
.
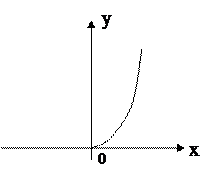 |
б) 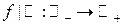 ;
; 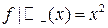 для
для 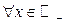
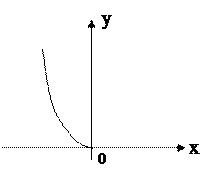
Определение. Функция 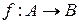 называется инъекцией (инъективным отображением), если она обладает свойством:
называется инъекцией (инъективным отображением), если она обладает свойством:
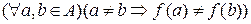
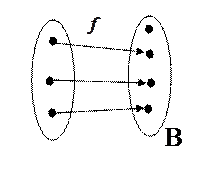 |
Рис. 1.
Используя закон контрапозиции можно дать другое определение инъекции, равносильное приведённому выше.
Функция 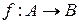 называется инъекцией (инъективным отображением), если она обладает свойством:
называется инъекцией (инъективным отображением), если она обладает свойством: 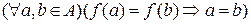
Определение. Функция 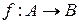 называется сюръекцией, если
называется сюръекцией, если 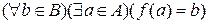 . Сюръекция – это отображение «НА».
. Сюръекция – это отображение «НА».
 |
Рис.2.
В чём разница рисунков?
На рисунке 1 к некоторым точкам проведены стрелки. Если к точке проведена стрелка, то только одна. На рисунке 2 к каждой точке множества 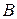 проведена стрелка. К некоторым точкам множества
проведена стрелка. К некоторым точкам множества 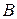 может быть проведено несколько стрелок.
может быть проведено несколько стрелок.
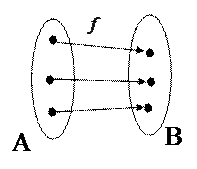 Определение. Функция
Определение. Функция 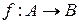 называется биекцией (взаимнооднозначным отображением), если
называется биекцией (взаимнооднозначным отображением), если 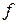 одновременно инъективно и сюръективно.
одновременно инъективно и сюръективно.
Задача (УИРС).
Пусть 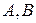 - конечные множества.
- конечные множества. 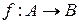 - биекция.
- биекция.
Что можно сказать про мощность множеств?
Пример. Определить вид следующих функций.
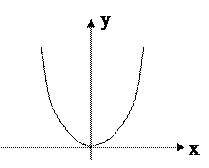 1.
1. 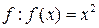 ;
; 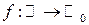
- не является инъекцией,
- сюръекция,
- не является биекцией.
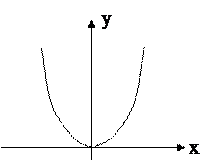 2.
2. 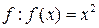 ;
; 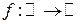
- не является инъекцией,
- не является сюръекцией,
- не является биекцией.
3. 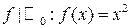 ;
; 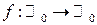
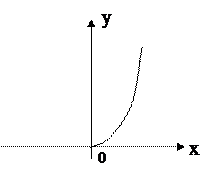
- инъекция,
- сюръекция,
- биекция.
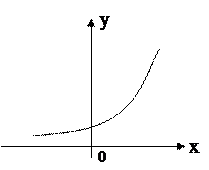 4.
4. 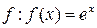 ;
; 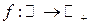
- инъекция,
- сюръекция,
- биекция,
Задача. (УИРС)
Пусть 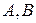 - конечные множества.
- конечные множества.  ,
, 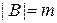 .
.
Сколько существует инъекций 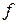 таких, что
таких, что 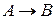 ?
?
Сколько существует сюръекций 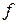 таких, что
таких, что 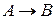 ?
?
Сколько существует биекций 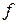 таких, что
таких, что 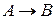 ? Какое условие существования этих функций?
? Какое условие существования этих функций?
Определение. Пусть 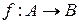 ,
, 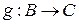 . Композицией функций
. Композицией функций  и
и 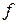 (обозначается
(обозначается 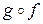 ) называется такая функция, что её значение
) называется такая функция, что её значение 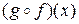 определяется как
определяется как 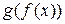 для
для 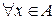 .
.
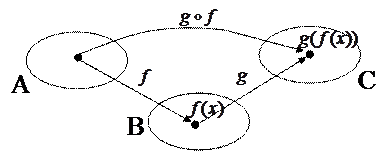 |
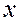
Областью определения композиции является множество А.
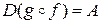
Множеством значений композиции является множество С.
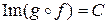 ,
,
 - внешняя функция,
- внешняя функция, 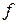 - внутренняя функция.
- внутренняя функция.
Сначала на элементы действует внутренняя, а затем внешняя функция.
|
|
|
|
|
Дата добавления: 2015-03-31; Просмотров: 1855; Нарушение авторских прав?; Мы поможем в написании вашей работы!