Дисконтирование финансовых рент

Во многих случаях потоки платежей необходимо дисконтировать к некоторому начальному моменту. Результат S(0) приведения потока к моменту

t = 0 называется современной или приведенной величиной (present value) и обозначается PV. Пусть по-прежнему рассматривается поток платежей 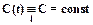при t = 1,2,..,k,..,n. Обозначим через 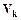дисконт-фактор для платежа, выполненного в момент t = k,то есть

,

где - дисконтированная величина платежа C(k). Тогда сумма всех величин дисконтированных платежей C(k) к моменту t = 0 равна

.

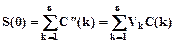Для финансовой ренты с использованием для дисконтирования схемы сложных процентов имеем

, .

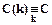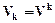Здесь по-прежнему предполагаются ежегодные платежи (поток платежей имеет период 1 год), символом V обозначен годовой дисконт-фактор. В результате можно записать

, .

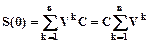Последовательность СV, СV², СV³,...,СVⁿ может быть рассмотрена как геометрическая прогрессия a₀, a₁, a₂,..., a_n-1 со знаменателем q = V и первым членом a₀ = СV. Тогда

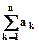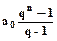= = = или

.

Поскольку , то после подстановки нетрудно получить

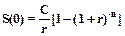
В электронной таблице Excel для расчета приведенной величины S(0) предусмотрена табличная функции

S(0) = ПЗ(r;n;C)

Определим предел приведенной величины S(0) при количестве периодов (лет), стремящемся к бесконечности. Так как (1+r) > 1, то

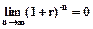и .

Из полученного соотношения следует, что для любого конечного срока n приведенная величина S(0) (дисконтированный поток платежей) такова, что должно выполняться условие .

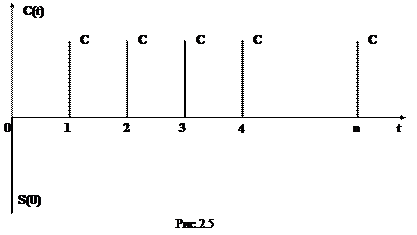
Одним из примеров рассматриваемого потока платежей является погашение долгосрочного кредита. Кредит размером S(0) выдается в момент t = 0 и погашается в течение n лет равными взносами С. При заданной процентной ставке r кредит может быть представлен как дисконтированный к моменту t = 0 поток платежей (рис.2.5).

В этих условиях возникает необходимость расчета различных параметров кредита. Размер периодического платежа по погашению кредита С может быть определен из выражения для приведенной величины S(0)

.

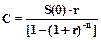Соответствующая функция электронной таблицы Excel имеет вид

С = ППЛАТ(r;n;S(0)).

Количество платежей n (количество периодов потока платежей) также определяется из выражения для приведенной величины S(0).

Действительно, из этого выражения следует

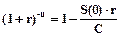или .

Поскольку функция ln существует лишь для положительных аргументов, то из последнего выражения вновь следует требование 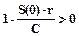или . В противном случае кредит S(0) никогда не будет погашен периодическими платежами С.

Для расчета количества платежей можно использовать функцию Excel n = КПЕР(r;C;S(0)).

Если требуется рассчитать процентную ставку r, под которую следует предоставить кредит в размере S(0) с ежегодными выплатами размером С и сроком погашения n лет, то из выражения для S(0) следует

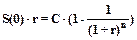или .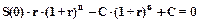

Для расчета корня этого нелинейного уравнения в электронной таблице Excel имеется функция

r = НОРМА(n;C;S(0)) ·.

Практически важной задачей, возникающей в отношениях заемщика и кредитора, является расчет досрочных выплат заемщика. Сформулируем следующую задачу. Пусть получен кредит размером S(0) с ежегодным возвратом в течение n лет. В этом случае ежегодный платеж заемщика равен 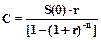. Пусть, кроме того, в момент t = k < n заемщик решил досрочно полностью расплатиться с кредитором. Задача заключается в расчете суммы S⁰(k), которую должен вернуть заемщик в момент t = k. Графически данная ситуация может быть иллюстрирована следующим образом (рис.2.6).

S^0(k)

C

C

t

Рис.2.6

	k
		k+1

Для решения этой задачи будем полагать, что кредитор дал в долг заемщику сумму S(0) в момент t = 0 на лет под r процентов годовых Тогда в момент t = k заемщик выплатит k раз ежегодно платеж С и ему предстоит в течение 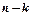лет выплатить ежегодные платежи С Дисконтируя эти платежи к моменту , получим

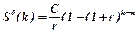, где

.

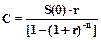В электронной таблице Excel можно воспользоваться функцией

S⁰(k) =ПЗ(r;n-k;С).

Пример. Пусть выдан кредит в сумме 100 млн.руб. сроком на 5 лет под 10 процентов годовых. Требуется рассчитать ежегодный возврат кредита и суммы досрочного погашения кредита для каждого из моментов t = k, k = 1,2,3,4,5.

Воспользуемся для расчетов электронной таблицей Excel.. Имеем

C = ППЛАТ(r;n;S(0))= ППЛАТ(10%;5;100) = 26.4 млн.руб.

S⁰(1) = ПЗ(r;n-k;ППЛАТ(r;n;S(0))) = ПЗ(10%;4;ППЛАТ(10%;5;100)) = 83.6, S⁰(2) = ПЗ(10%;3;ППЛАТ(10%;4;100)) = 65.6,

S⁰(3) = ПЗ(10%;2;ППЛАТ(10%;5;100)) = 45.8,

S⁰(4) = ПЗ(10%;1;ППЛАТ(10%;5;100)) = 24,

S⁰(5) = ПЗ(10%;0;ППЛАТ(10%;5;100)) = 0.

Эти результаты можно интерпретировать следующим образом. Если заемщик хочет погасить кредит в конце 1-го года, то он должен выплатить кредитору периодический платеж 26,4 млн.руб и сумму досрочного погашения кредита 83,6 млн.руб. При желании заемщика досрочно рассчитаться в конце 2-го года, схема его платежей следующая: в конце 1-го года - 26,4 млн.руб., в конце 2-го года - 26,4 млн.руб. и плюс 65,6 млн.руб. и т.д.

Дата добавления: 2015-03-31