Двусторонние потоки платежей

Двусторонним называется поток платежей, который предполагает распределенные во времени переходы денежных сумм от одного владельца к другому. С позиций одного из участников такой многоэтапной финансовой операции можно считать, что поступление денежных средств к нему в момент t = t_k соответствует положительному платежу (C(t_k) > 0), а выплата второму участнику операции соответствует отрицательному платежу (C(t_k) < 0). Графическое представление такого потока платежей приведено на рис.2.9.

Для оценки эффективности в целом финансовой операции, представляемой нерегулярным двусторонним потоком платежей, используются различные показатели. Один из них, называемый чистой приведенной величиной (NPV - net present value), рассчитывается как приведенная (современная) величина потока по формуле

NPV = S(0) = ,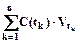

где C(t_k) - поступления или выплаты потока, рассматриваемые как платежи потока с соответствующим знаком. Операция считается эффективной для участника, если показатель NPV для него является положительным.

При неизменности годовой процентной ставки r и использовании схемы сложных процентов

NPV = S(0) =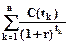

Заметим, что знак показателя NPV не зависит от момента времени, к которому приводится поток платежей. Действительно, пусть момент, к которому дисконтируется поток, изменился на величину t₀.

Обозначим

NPV₀ = .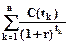

Для новой точки отсчета (момента времени t₀ , к которому приводится поток) величина NPV равна

NPV = = =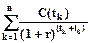

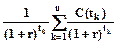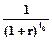
= = NPV_{0 .}

Поскольку множитель 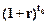> 0 для любого t₀ , знак инвариантен (не зависит) к сдвигу момента приведения t₀. Таким образом, для оценки эффективности любой многоэтапной финансовой операции достаточно рассчитать NPV для любого момента приведения и определить знак этого показателя.

Пример. Банк предоставляет фирме в течение двух лет кредит ежегодными платежами по 100 млн.руб. под процентную ставку 10 % годовых. Фирма возвращает долги в конце 2, 3 и 4-го годов платежами соответственно 100, 100 и 50 млн.руб. Каково значение показателя NPV для банка?

Изобразим поток платежей в графической форме (рис.2.10).

Будем считать, что моментом приведения потока (t = 0) является момент выдачи первого кредита банком.

Тогда

NPV = -100-100/(1+0.1) +100/(1+0.1)² +100/(1+0.1)³+ 50/(1+0.1)⁴ =1.018 млн.руб.

Поскольку NPV > 0, финансовая операция выгодна для банка.

В электронной таблице имеется финансовая функция НПЗ, с помощью, которой рассчитывается данный показатель для частного вида нерегулярных потоков платежей, а именно потока с периодическими платежами (положительными и отрицательными) произвольной величины. Дополнительно предполагается, что первый платеж потока имеет место в конце первого периода, а приведение осуществляется к началу первого периода. Процентная ставка на весь срок операции считается неизменной. Формат этой функции имеет вид

НПЗ(r_T,<интервал клеток>).

Если требуется момент приведения потока совместить с моментом первого платежа, то полученное с помощью табличной функции значение NPV следует умножить на величину 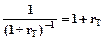. Здесь Т - период между платежами периодического потока.

Для рассмотренного выше примера поток платежей является нерегулярным, но периодическим с периодом 1 год. Процентная ставка на этом периоде задана и равна r_T = r = 0.1. Если в клетки A1:A5 таблицы Excel поместить значения платежей данного потока, то есть числа -100,-100,100,100,50 соответственно, то в клетке с формулой НПЗ(0.1,A1:A5) будет получено значение 0.925. Для приведения этой величины к моменту выдачи первого кредита (первого платежа потока) следует умножить эту величину на (1+r) = (1+0.1) = 1.1, в результате чего вновь будет получена величина NPV = 1.018.

Отметим, что электронная таблица Excel 7.0 располагает возможностью расчета показателя NPV и для непериодических потоков платежей. Формат этой функции имеет вид

ЧИСТНЗ(r;значения;даты).

Здесь: r -годовая процентная ставка; значения -интервал клеток, в которые помещаются значения последовательных платежей потока; даты - интервал клеток, в которые помещены даты последовательных платежей потока. В отличие от ранее рассмотренных последняя функция осуществляет приведение потока к моменту первого платежа.

С помощью знака показателя NPV можно оценить эффективность одной многоэтапной финансовой операции. Однако с помощью этого показателя невозможно сопоставить эффективности двух различных операций и выбрать более выгодную из них. Для сопоставления эффективностей различных операций, описываемых нерегулярными потоками платежей, используется показатель, называемый внутренней эффективностью операции, эффективной ставкой операции, внутренней нормой доходности операции. Этот показатель обычно обозначается IRR (internal rate of return). Внутренняя эффективность операции равна процентной ставке r_ef, при которой NPV соответствующего потока равен нулю. Из этого определения следует, что IRR = r_ef определяется как корень уравнения

NPV = 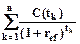= 0.

Следует заметить, что значение r_ef не зависит от того, к какому моменту времени приводится (дисконтируется) поток платежей при расчете NPV. Действительно, ранее было установлено, что при изменении момента приведения потока значение NPV изменяется в соответствии с соотношением 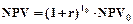. Из этого соотношения следует, что если NPV равно нулю для какого-либо момента приведения потока, то этот показатель равен нулю и для любого другого момента приведения, смещенного относительно исходного момента на произвольную величину t₀.

Решение нелинейного уравнения для определения значения IRR = r_ef в общем случае сопряжено с некоторыми сложностями. В электронной таблице Excel для выполнения этой операции предусмотрена табличная функция, которая рассчитывает значение IRR для периодического нерегулярного потока. Формат этой функции имеет вид

ВНДОХ(<интервал клеток>, r₀). Здесь r₀ - начальное приближение для r_ef, которое по умолчанию принимается равным 0.1. Как и для функции NPV <интервал клеток> здесь означает перечень клеток таблицы, в которые заносятся значения платежей периодического потока со своими знаками.

Кроме того, Excel содержит финансовую функцию, предназначенную для расчета внутренней эффективности операции в более общем случае непериодического потока. Эта функция имеет вид

ЧИСТВНДОХ(значения;даты;r₀).

Аргументы этой функции совпадают с соответствующими аргументами функции ЧИСТНЗ.

При сопоставлении двух многоэтапных финансовых операций предпочтение отдается той из них, для которой значение внутренней эффективности операции IRR больше.

Пример. Сопоставим эффективности двух периодических нерегулярных потоков платежей с одинаковым периодом. Первому из потоков соответствуют платежи в конце каждого периода (-100,-100,100,100,50), для второго потока эти платежи равны (-100,-200,120,140,100).

Для расчета IRR каждого потока воспользуемся электронной таблицей Excel. В клетки A1:A5 поместим составляющие первого потока, а в клетки B1:B5 - платежи второго потока. В клетку А6 внесем формулу ВНДОХ(0.1,A1:A5), а в клетку B6 формулу ВНДОХ(0.1,B1:B6). В результате расчета получим, что для первого потока IRR = 0.103, а для второго потока IRR = 0.084. Следовательно, первый поток является предпочтительным для рассматриваемого участника операции.

Пусть теперь следует определить внутреннюю эффективность операции, которой соответствует поток платежей (-100,-200,250,120), последовательные платежи которого осуществляются в моменты времени (01.01.05;01.08.06;01.05.07;01.12.08). С этой целью введем в клетки A1:A4 таблицы Excel значения платежей потока, а в клетки В1:В4 - значения соответствующих дат. Если в клетку А6 будет введена формула

= ЧИСТВНДОХ(A1:A4;B1:B4;0,1), то в результате расчетов в этой клетке будет получена величина IRR = 0,124156.

В заключение этого раздела упомянем об одной практически важной задаче, которая возникает в процессе взаимоотношений кредитора и заёмщика. Речь идёт о тех ситуациях, когда кредит предоставляется под определённую процентную ставку, но с комиссией. В Приложении 2.3 приведены соотношения, которые позволяют заёмщику выбрать наиболее выгодный для него вариант кредита в этих условиях при наличии нескольких альтернатив.

Приложение 2.1

Установим соотношения между зависимостями процентных ставок от периода Т по схемам простых и сложных процентов.

Имеем 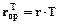, 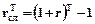. При .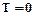

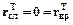Производные по Т при Т = 0

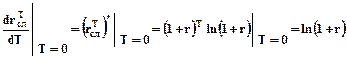
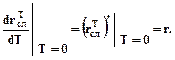
Докажем, что ln(1 + r) < r для любого r > 0.

Рассмотрим ряд

e^r = 1 + r + 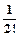r² +... + 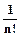rⁿ +...,

который сходится при любом значении r [А.Ф.Бермант, И.Г.Араманович. Краткий курс математического анализа для втузов. М., Наука, 1967,стр.674]. Последнее выражение можно представить

e^r = 1 + r + Q,

где (при r > 0)

Q = 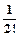r² +... + 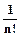rⁿ +... +...> 0.

Из приведенных соотношений следует

e^r > 1 + r.

Логарифмируя левую и правую часть этого неравенства, получим

r > ln(1 + r),

что и требовалось доказать.

Таким образом

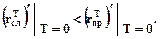
Поскольку при Т = 0 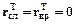, то это значит, что в окрестности точки Т = 0 при положительных Т .

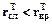Функция 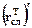является монотонно возрастающей.

Действительно, при t > 0

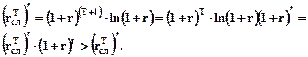
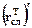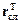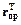Поскольку = r и не зависит от Т, то из графического представления зависимостей и следует, что наклон касательной к графику функции 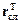, будучи при Т 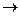0 меньше r, с ростом Т увеличивается неограниченно и монотонно, и при некотором Т станет больше r. При дальнейшем увеличении Т график 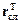пересечет график 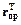. При Т, превышающем абсциссу точки пересечения 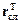> 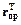. Из приведенных соображений следует, что точка пересечения графиков 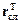и 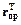единственная. Так как при Т = 1

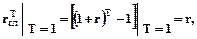
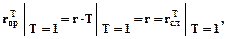
то именно Т = 1 является единственной точкой пересечения графиков 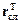и 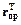. То есть

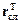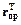< при 0<T<1,

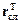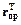> при T>1.

Приложение 2.2

Дата добавления: 2015-03-31