Блок 7Д. Традиционные методы оценки риска

Цели:

= рассмотреть вероятностный подход к количественной оценке риска;

= изучить сущность и способы расчетов традиционных статистических показателей количественной оценки риска – размах вариации, дисперсия, среднее квадратическое отклонение и размах вариации.

Финансовый риск, как и любой риск, имеет матема­тически выраженную вероятность наступления поте­ри, которая опирается на статистические данные и мо­жет быть рассчитана с достаточно высокой точностью.

Эффективность любой финансовой или хозяйственной операции и величина сопутствующего ей риска взаимосвязаны. Также существует взаимосвязь между риском и доходностью рассматриваемого проекта.

Как правило, методы оценки риска и доходности различных инвестиционных проектов производятся для сравнения двух или более проектов, а затем выбора наилучшего или наиболее подходящего для данного инвестора.

Для решения этой задачи надо количественно определить величину финансового риска и сравнить степень риска альтер­нативных вариантов. Степень риска в большинстве случаев может быть достаточно точно оценена, а так же определена величина доходности предлагаемого проекта, соответствующая данному риску.

Чтобы количественно определить величину финансо­вого риска, необходимо знать все возможные послед­ствия какого-нибудь отдельного действия и вероят­ность самих последствий. Вероятность означает воз­можность получения определенного результата.

При­менительно к экономическим задачам методы теории вероятности сводятся к определению значений вероятности наступления событий и к выбору из возможных событий самого предпочтительного исходя из наи­большей величины математического ожидания.

Иначе говоря, математическое ожидание какого-либо собы­тия равно абсолютной величине этого события, ум­ноженной на вероятность его наступления.

Пример. Имеются два варианта вложения капита­ла. Установлено, что при вложении капитала в мероп­риятие А получение прибыли в сумме 15 тыс. руб. — вероятность 0,6; в мероприятие Б получение прибыли в сумме 20 тыс. руб. — вероятность 0,4. Тогда ожида­емое получение прибыли от вложения капитала (т.е. математическое ожидание) составит:

по мероприятию А 15 • 0,6 = 9 тыс. руб.;

по мероприятию Б 20 • 0,4 = 8 тыс. руб.

Вероятность наступления события может быть определена объективным методом или субъективным.

Объективный метод определения вероятности основан на вычислении частоты, с которой происходит данное событие.

Например, если известно, что при вложении капитала в какое-либо мероприятие прибыль в сумме 15 тыс. руб. была получена в 120 случаев из 200, то вероятность получения такой прибыли составляет 0,6 или 60% (120:200).

Субъективный метод базируется на использовании субъективных критериев, которые основыва­ются на различных предположениях. К таким пред­положениям могут относиться суждение оценивающе­го, его личный опыт, оценка эксперта, мнение финан­сового консультанта и т.п.

Величина риска или степень риска измеряется дву­мя критериями:

1) среднее ожидаемое значение;

2) колеблемость (изменчивость) возможного ре­зультата.

Среднее ожидаемое значение — это то значение величины события, которое связано с неопределенной ситуацией. Среднее ожидаемое значение является сред­невзвешенным для всех возможных результатов, где вероятность каждого результата используется в каче­стве частоты или веса соответствующего значения. Среднее ожидаемое значение измеряет результат, ко­торый мы ожидаем в среднем.

Пример. Если известно, что при вложении капитала в мероприятия А из 120 случаев прибыль 12,5 тыс. руб. была получена в 48 случаях (вероятность 0,4), прибыль 20 тыс. руб. — в 42 случаях (вероятность 0,35) и при­быль 12 тыс. руб. — в 30 случаях (вероятность 0,25), то среднее ожидаемое значение выразилось в 15 тыс. руб.

[(12,5 • 0,4) + (20 • 0,35) + (12 • 0,25)].

Изменчивость (колеблемость) возможного результата представ­ляет собой степень отклонения ожидаемого значения от средней величины.

Рисковые активы характеризуются вероятностными значениями получения результата. Если известны все возможные значения результата (здесь имеется в виду значение дохода – в абсолютном выражении или относительная величина – доходность) и вероятности получения этих значений (сумма вероятностей при этом будет равняться единице), то такое представление результата носит название вероятностного распределения.

Вероятностное распределение может быть представлено в виде таблицы или графически. Например, если рассматривается актив А и известны возможные цены его продажи через год, то вероятностное распределение может быть представлено в виде таблицы.

Предположим, что объем инвестиций в данный актив составил 350 денежных единиц. Существует три варианта продажи данного актива:

-за 420 денежных единиц с вероятностью 25%;

-за 400 денежных единиц с вероятностью 50%;

-за 380 денежных единиц с вероятностью 25%.

Рассчитав доход от продажи актива как разность между ценой продажи и инвестированными в него средствами, а также произведя расчет доходности по формуле:

,

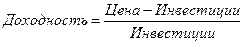получим следующую таблицу:

Цена продажи	Вероятность	Доход	Доходность
	25%		20%
	50%		14,3%
	25%		8,6%

Ожидаемое значение результата определяется как сумма произведений возможных значений результата на соответствующие значения вероятностей.

Исходя из вышеуказанного примера получаем следующее значение ожидаемой доходности:

20*0,25+14,3*0,5+8,6*0,25=14,3%.

При предположении о возможности указать вероятность каждого исхода можно построить график непрерывного распределения вероятности. Чем более заостренной будет форма кривой непрерывного распределения вероятности, тем больше вероятность, что фактическая доходность будет ближе к ожидаемому значению и тем ниже риск принимаемого решения.

Во многих исследованиях, включающих оценку вероятности предполагается, что вероятностное распределение является нормальным[2]:

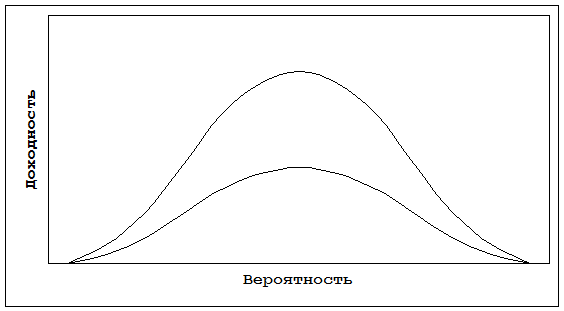
Нормальное распределение вероятностей предполагает, что среднему состоянию доходности соответствует самая большая вероятность (при этом данная величина доходности является одновременно и средним арифметическим двух крайних значений), а далее значения вероятностей равномерно уменьшаются при удалении от нормы как в одну, так и в другую сторону, стремясь к нулю в крайних положениях. Сумма всех вероятностей при этом равна 1.

Нормальное распределение достаточно полно отражает реальную ситуацию и дает возможность, используя ограниченную информацию, получать числовые характеристики, необходимые для оценки степени риска того или иного проекта.

Как было отмечено, количественно риск может быть охарактеризован как некий показатель, измеряющий вариабельность дохода или доходности. Таким образом, для этой цели может быть использован ряд, как относительных, так и абсолютных, статистических коэффициентов. Традиционными в этом плане являются: размах вариации, дисперсия, среднее квадратическое отклонение и коэффициент вариации.

Размах вариации - это разность между максимальным и минимальным значениями признака данного ряда.

Этот показатель имеет много недостатков, основными из них являются:

- этот показатель дает грубую оценку степени вариации значений признака;

- он является абсолютным показателем, и потому его применение в сравнительном анализе весьма ограничено;

- его величина слишком зависит от крайних значений ранжированного ряда.

Считается, что чем выше значение размаха вариации, тем выше степень риска по данному проекту, т.е. наилучшим (под наилучшим подразумевается проект с наименьшей степенью риска) окажется тот проект, у которого значение размаха вариации окажется минимальным.

Дисперсия является средним квадратом отклонений значений признака от его средней величины и рассчитывается по следующей формуле:

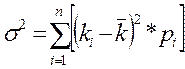, где

- k_i – значение доходности по данному активу;

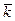- - среднее, ожидаемое значение доходности, рассчитываемое по формуле: ;

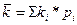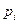- - вероятность, соответствующая данному значению доходности;

- n – число возможных отклонений от ожидаемого значения.

Дисперсия измеряется в тех же единицах, что и результат - в процентах, если в качестве результата рассматривается доходность, и в денежных единицах, если в качестве результата рассматриваются денежные потоки, но возведенных в квадрат.

Среднее квадратическое отклонение показывает среднее отклонение значений варьирующего признака относительно центра распределения, в данном случае – средней арифметической. Этот показатель рассчитывается по формуле:

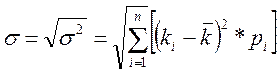, где

- k_i – значение доходности по данному активу;

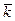- - среднее, ожидаемое значение доходности, рассчитываемое по формуле: ;

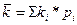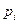- - вероятность, соответствующая данному значению доходности;

n – число возможных отклонений от ожидаемого значения.

Среднее квадратическое (стандартное) отклонение более удобно, чем дисперсия, так как измеряется в тех же единицах, что и результат, что облегчает сравнение и анализ риска различных активов, в отличие от дисперсии.

Для оценки риска через стандартное отклонение необходимо:

- рассчитать абсолютное отклонение возможных значений доходности от ожидаемого значения;

- возвести в квадрат полученное отклонение;

- домножить квадрат отклонений на соответствующее значение вероятности.

Сумма произведений составит значение дисперсии, после извлечения квадратного корня получим среднее квадратическое отклонение.

Коэффициент вариации – относительная величина, которая рассчитывается по формуле:

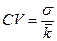, где

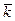- - среднее, ожидаемое значение доходности;

- σ – среднее квадратическое отклонение.

Если сравниваются активы, имеющие различную доходность, то по значению среднего квадратического отклонения нельзя сделать вывод, какой из них является более рискованным.

Для сравнения активов с различной доходностью по степени риска необходимо уравнять разброс с учетом доходности, т.е. рассчитать риск на единицу доходности.

Таким нормированным показателем степени риска являетсякоэффициент вариации, как отношение среднего квадратического отклонения к ожидаемому значению доходности.

Чем выше коэффициент вариации, тем выше риск владения активом. Такое утверждение верно при равной ликвидности рассматриваемых активов.

Такие показатели, как дисперсия и среднее квадратическое отклонение, обладают одним общим недостатком: это абсолютные показатели, значения которых существенно зависят от абсолютных значений исходного признака ряда. Поэтому большее применение имеет коэффициент вариации.

В отношении оценки риска финансовых активов, как отмечалось выше, риск может оцениваться вариабельностью либо дохода либо доходности.

Поскольку доход в абсолютной оценке может существенно варьировать при сравнительном анализе различных финансовых активов, то принято в качестве базисного показателя, характеризующего результативность операции с финансовым активом, использовать не доход, а доходность. Доходность не зависит от размера инвестиции и потому сопоставима в пространственно-временном разрезе.

Также, основными показателями оценки риска на рынке капитала являются дисперсия и среднее квадратическое отклонение. Распространенность и пригодность в сравнительном анализе этих статистик в данном случае объясняется тем обстоятельством, что базисным показателем при расчетах является доходность, т.е. относительный показатель, сопоставимый как в динамике, так и по различным видам активов. Поэтому независимо от анализируемых активов соответствующие им показатели доходности и дисперсии однопорядковы, и нет острой необходимости применять в оценке коэффициент вариации.

При оценке риска используют модификации формул дисперсии и среднего квадратического отклонения, в которых весами значений ожидаемой или требуемой доходности являются вероятности их появления.

Необходимо отметить еще одну очень важную особенность анализа риска и доходности.

Как и любая вероятностная категория, риск может быть оценен по-разному. Однако, речь должна идти не только и не столько о различии алгоритмов и критериев оценки, приведенных выше, сколько о том, рассматривается ли данный финансовый актив изолированно или как составная часть набора активов.

При рассмотрении актива изолированно никаких особых проблем теоретического характера в принципе не возникает, а его рисковость может быть измерена с помощью одного из рассмотренных выше показателей.

Также следует отметить, что наиболее часто варианты доходности по проекту рассматриваются по оптимистическому, нормальному и пессимистическому прогнозам.

Рассмотрим все вышеуказанные показатели на конкретном гипотетическом примере.

В таблицах представлены данные по двум проектам:

проект А

Прогноз	Доходность	Вероятность
Оптимистический	100%	20%
Нормальный	70%	50%
Пессимистический	20%	30%

проект Б

Прогноз	Доходность	Вероятность
Оптимистический	70%	30%
Нормальный	50%	40%
Пессимистический	40%	30%

Теперь, исходя из имеющихся данных, произведем оценку риска с используя названные методы.

Рассчитаем размах вариации по двум проектам:

проект А: РВ=100-20=80

проект Б: РВ=70-40=30.

По данному показателю наиболее предпочтительным является проект Б, имеющий меньшее значение размаха вариации. Но надо учесть, что данный коэффициент не учитывает вероятность наступления той или иной ситуации, благодаря которой доходность будет изменяться и большую или меньшую сторону.

Рассчитаем значение ожидаемой доходности:

для проекта А: 100*0,2+70*0,5+20*0,3=20+35+6=61%

для проекта Б: 70*0,3+50*0,4+40*0,3=21+20+12=53%.

Рассчитаем значения дисперсии:

для проекта А:

Вероятность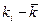
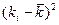
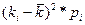
0,2	100-61=39		304,2
0,5	70-61=9		40,5
0,3	20-61=-41		504,3

Таким образом, σ²=304,2+40,5+504,3=849.

для проекта Б:

Вероятность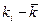
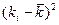
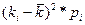
0,3	70-53=17		86,7
0,4	50-53=-3		3,6
0,3	40-53=-13		50,7

Таким образом, σ²=86,7+3,6+50,7=141.

В итоге получается, что средний уровень доходности по проекту А выше (61% в отличие от 53% по проекту Б), но в то же время дисперсия, показывающая уровень риска, указывает на то, что проект А является более рисковым, чем проект Б. Таким образом, если бы инвестор ориентировался бы только на уровень доходности, не учитывая фактор риска во время анализа проекта, он выбрал бы проект А, т.к. он наиболее доходный. Но если принимать во внимание значение уровня риска, то инвестор выбрал бы скорее всего проект Б, т.к. степень риска по нему значительно ниже при несущественном уменьшении доходности (всего на 8%, 61%-53%=8%).

Рассчитаем значение среднего квадратического отклонения:

по проекту А: √ σ²=29,14

по проекту Б: √ σ²=11,87.

Полученные значения также указывают на то, что уровень риска по проекту Б ниже, чем по проекту А.

И, в заключение, рассчитаем коэффициент вариации:

для проекта А:

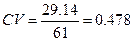
для проека Б:

.

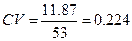Коэффициент вариации также показывает, что осуществление проекта А является более рискованным, чем осуществление проекта Б.

Следует также отметить, что существуют разные типы инвесторов. Имеются ввиду инвесторы, склонные к риску, и инвесторы, не склонные к риску.

Так, инвесторы, склонные к риску и ориентированные ни максимизацию прибыли при осуществлении своего проекта, скорее всего выберут проект А. Проект же Б покажется более привлекательным второй категории инвесторов, т.е. тем, которые не склонны к риску.

Таким образом, конечный выбор того или иного проекта зависит не только от данных и показателей, полученных в ходе анализа риска и доходности сравниваемых проектов, но и от личности инвестора, т.е. лица, принимающего решения.

Контрольные вопросы, задания и тесты:

1. Какова математическая возможность оценки финансового риска?

2. Что такое математическое ожидание?

3. В чем заключается субъективный подход к оценке финансового риска?

4. Назовите статистические методы оценки финансового риска и дайте их характеристику.

Задание 1. Инвестиционные проекты имеют следующие характеристики:

Прогноз	Проект А	Проект Б	Проект В
%	доходность	вероятность	доходность	вероятность	доходность	вероятность
оптимистический
нормальный
пессимистический

Оцените финансовый риск реализации каждого из проектов.

Тест 1. Выберите правильный ответ:

Если сравниваются активы, имеющие различную доходность, то сделать вывод, какой из них является наиболее рискованным по значению стандартного отклонения:

1. можно;

2. нельзя;

3. требуется дополнительная информация.

4. правильный ответ отсутствует.

Тест 2. Выберите правильный ответ:

Коэффициент вариации – это:

1. относительная величина;

2. абсолютная величина;

3. универсальная величина;

4. правильный ответ отсутствует.

МОДУЛЬ 7. ВЫВОДЫ.

Изучив данный модуль Вы должны понимать сущность финансовых рисков и особенности их реализации на предприятии.

Теперь Вы можете:

= дать характеристику финансовых рисков;

= раскрыть сущность финансовых рисков с точки зрения принятия на предприятии типа финансового решения;

= дать характеристику, показать компенсационные возможности по финансовым рискам собственников, кредиторов и менеджеров предприятия;

= провести математическую оценку финансового риска.

Литература к Модулю 7.

1. Балабанов И.Т. «Риск-менеджмент», М., «Финансы и статистика», 1996 г.

2. Воронцовский А.В.

3. Ковалев В.В. «Финансовый анализ», М., «Финансы и статистика», 2000 г.

4. Ковалев В.В., Ковалев Вит.В. «Финансы предприятий», М., «Проспект», 2002 г.

[1] Финансово-промышленные группы в России: необходимость, сущность, перспективы. - Иркутск, 1999.

[2] Теплова Т.В. «Финансовый менеджмент: управление капиталом и инвестициями»

Дата добавления: 2015-03-31