Неравенство Чебышева

Для случайной величины 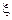, имеющей ограниченную дисперсию , и для любого справедливо неравенство Чебышева 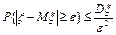Док-во: Пусть .

Докажем неравенство для непрерывной случайной величины 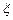с плотностью распределения . Вероятность 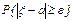есть вероятность попадания с.в. 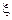в область, лежащую вне промежутка [ ]. Можно записать

т.к. область интегрирования можно записать в виде . Имеем

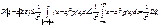
т.к. интеграл от неотрицательной функции при расширении области интегрирования может возрасти.

Аналогично доказывается неравенство Чебышева и для дискретной случайной величины 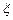, только интегралы (вида ) заменяются соответствующими суммами (вида ).

Отметим, что неравенство Чебышева часто используется для противоположного события:

27.Полигон и гистограмма.

Для наглядности строят различные графики статистического распределения. Например график эмпирической функции распределения, полигон и гистограмму.

Полигоном частот называют ломанную, отрезки которой соединяют точки c координатами: Для изучения непрерывного признака строится гистограмма. Для этого интервал 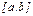, где 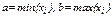, делится на несколько частичных интервалов одинаковой длины h. Затем подсчитывается число вариант n_i, попавших в каждый интервал.

Гистограмма – фигура, состоящая из прямоугольников, основанием которых служат частичные интервалы длины , а высоты .Тогда площадь -го прямоугольника равна , а площадь всей гистограммы 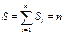, где - объем выборки.

Аналогично строится гистограмма относительных частот. При этом вдоль оси Oy откладываются . Тогда площадь i -го прямоугольника равна 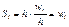. А площадь всей гистограммы 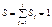.Аналогичным свойством нормировки обладает плотность распределения вероятностей. Таким образом, гистограмма служит для оценки вида плотности вероятности.

Полигон распределения

Дата добавления: 2015-03-31