
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Точечное оценивание
|
|
|
|
Статистической оценкой называется любая функция выборки
 .
.
Точечной оценкой называется оценка, которая дается одним числом.
Для того, чтобы статистическая оценка давала хорошее приближение оцениваемому параметру θ, она должна обладать определенными свойствами.
Оценка  называется несмещенной, если ее матожидание равно оцениваемому параметру
называется несмещенной, если ее матожидание равно оцениваемому параметру  .
.
Это свойство означает отсутствие ошибки одного знака.
Примеромнесмещенной оценки являетсявыборочное среднее для матожидания. Докажем это. Выборочные значения xi можно рассматривать как независимые случайные величины, взятые из одного и того же распределения.
Пусть 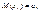
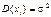 .
. 
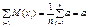 .
.
Примером смещенной оценки является выборочная дисперсия для теоретической дисперсии. Можно показать, что  .
.
Для того, чтобы получить несмещенную оценку 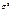 , вводится понятие исправленной выборочной дисперсии.
, вводится понятие исправленной выборочной дисперсии. 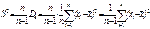 .
. 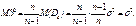
Оценка  параметра θ называется состоятельной, если для любого
параметра θ называется состоятельной, если для любого 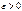
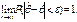
Состоятельность оценки означает, что при большом объеме выборки оценка приближается к истинному значению параметра θ (чем больше n, тем точнее оценка).
Оценки, обладающие свойством несмещенности и состоятельности, при ограниченном объеме выборки могут отличатся дисперсиями.
Чем меньше дисперсия оценки, тем меньше вероятность ошибки при вычислении  . Поэтому целесообразно, чтобы дисперсия оценки была минимальной, т.е. чтобы выполнялось условие
. Поэтому целесообразно, чтобы дисперсия оценки была минимальной, т.е. чтобы выполнялось условие 
Оценка, обладающая таким свойством, называется эффективной.
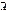 )=1 – P(A)5). Вероятность невозможного события 0: P(Ø)=0, так как m=0.6). Если событие А влечет за собой событие В, то P(A)
)=1 – P(A)5). Вероятность невозможного события 0: P(Ø)=0, так как m=0.6). Если событие А влечет за собой событие В, то P(A)  P(B). 7.) Для любого события А 0<P(A)<1
8. Для произвольгых событий В и С Р(В+С)<= P(B)+P(C)
3)Аксиоматическое определение вероятности
Пусть Ω - множество всех возможных исходов некоторого опыта (эксперимента). Согласно аксиоматическому определению вероятности, каждому события А (А подмножество множества Ω) ставится в соответствии некоторое числу р(А), называемое вероятностью события А, причем так, что выполняются следующие три условия (аксиомы вероятностей):
1)р(А)≥0
2)p(Ω)=1
3)аксиома сложения
P(B). 7.) Для любого события А 0<P(A)<1
8. Для произвольгых событий В и С Р(В+С)<= P(B)+P(C)
3)Аксиоматическое определение вероятности
Пусть Ω - множество всех возможных исходов некоторого опыта (эксперимента). Согласно аксиоматическому определению вероятности, каждому события А (А подмножество множества Ω) ставится в соответствии некоторое числу р(А), называемое вероятностью события А, причем так, что выполняются следующие три условия (аксиомы вероятностей):
1)р(А)≥0
2)p(Ω)=1
3)аксиома сложения
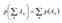 где Аi·Aj=Ω (i≠j), т.е. вероятность суммы попарно-несовместных событий равна сумме вероятностей этих событий.
Из этих трех аксиом, вытекают свойства вероятности:
1)р(Ø)=0, т.е. вероятность невозможного события равна нулю.
2)р(А)+р(Ā)=1
3)0≤р(А)≤1 для любого события А
4)р(А)≤р(В), если А подмножество В
5)
где Аi·Aj=Ω (i≠j), т.е. вероятность суммы попарно-несовместных событий равна сумме вероятностей этих событий.
Из этих трех аксиом, вытекают свойства вероятности:
1)р(Ø)=0, т.е. вероятность невозможного события равна нулю.
2)р(А)+р(Ā)=1
3)0≤р(А)≤1 для любого события А
4)р(А)≤р(В), если А подмножество В
5) 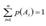 , если
, если  и Аi·Aj=Ø, i≠j
Если множество Ω состоит из n равновозможных элементарных событий, то вероятность события А определяется по формуле классического определения вероятности:p(A)=m/n
где m - число случаев (элементов), принадлежащих множеству В (число блогаприятствующих событию А исходов), n - число элементов множества Ω (число всех исходов опыта).
8. Предельные теоремы в схеме БернуллиПри больших n применение формулы Бернулли затруднительно из-за сложности вычисления факториалов и степеней. В этом случае используются приближенные формулы.
Рассмотрим 2 случая:
1.
и Аi·Aj=Ø, i≠j
Если множество Ω состоит из n равновозможных элементарных событий, то вероятность события А определяется по формуле классического определения вероятности:p(A)=m/n
где m - число случаев (элементов), принадлежащих множеству В (число блогаприятствующих событию А исходов), n - число элементов множества Ω (число всех исходов опыта).
8. Предельные теоремы в схеме БернуллиПри больших n применение формулы Бернулли затруднительно из-за сложности вычисления факториалов и степеней. В этом случае используются приближенные формулы.
Рассмотрим 2 случая:
1. 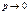 или
или  .
2. p Î(0,1) и не близко ни к нулю, ни к единице.
Теорема Пуассона.
Если в схеме Бернулли
.
2. p Î(0,1) и не близко ни к нулю, ни к единице.
Теорема Пуассона.
Если в схеме Бернулли 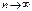 ,
,  так, что np® a, тогда
так, что np® a, тогда
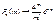 . Замечания:
1.
. Замечания:
1.  – среднее число появления события А в n испытаниях.
2. Как правило, теорему Пуассона применяют, когда
– среднее число появления события А в n испытаниях.
2. Как правило, теорему Пуассона применяют, когда  .
3. В конце книг по теор. вероятности есть таблицы для подсчета вероятности для различных a и m.
Локальная предельная теорема Муавра-Лапласа.
Если вероятность наступления некоторого события в n независимых испытаниях постоянна и равна p, pÎ(0,1), то вероятность того, что в этих испытаниях событие A наступит ровно m раз, удовлетворяет при n
.
3. В конце книг по теор. вероятности есть таблицы для подсчета вероятности для различных a и m.
Локальная предельная теорема Муавра-Лапласа.
Если вероятность наступления некоторого события в n независимых испытаниях постоянна и равна p, pÎ(0,1), то вероятность того, что в этих испытаниях событие A наступит ровно m раз, удовлетворяет при n 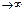 соотношению
соотношению
 где
где  Равномерно по всем m, для которых
Равномерно по всем m, для которых 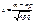 находится в каком-то конечном интервале;
Функция
находится в каком-то конечном интервале;
Функция 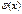 - плотность нормального распределения.
Интегральная предельная теорема Муавра-Лапласа.
Если m есть число наступлений события в n независимых испытаниях, в каждом из которых вероятность этого события равна p, причем p Î(0,1), то равномерно относительно a и b(−∞<a<b<+∞) n
- плотность нормального распределения.
Интегральная предельная теорема Муавра-Лапласа.
Если m есть число наступлений события в n независимых испытаниях, в каждом из которых вероятность этого события равна p, причем p Î(0,1), то равномерно относительно a и b(−∞<a<b<+∞) n 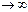 имеет место соотношение
имеет место соотношение  , Где
, Где 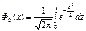 - функция Лапласа.
Замечания.
1. Функция Лапласа нечетная:
- функция Лапласа.
Замечания.
1. Функция Лапласа нечетная:
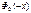 = -
= -  .
2. Функция Ф0(z) асимптотическая и при
.
2. Функция Ф0(z) асимптотическая и при 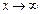 она быстро стремиться к 0,5. Это стремление настолько быстрое, что при
она быстро стремиться к 0,5. Это стремление настолько быстрое, что при 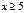
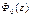 можно считать равной 0,5.
3. Плотность нормального распределения
можно считать равной 0,5.
3. Плотность нормального распределения 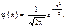 - четная функция.
13. Коэффициент корреляции и ковариация.
Коэффициентом корреляции называется
p(
- четная функция.
13. Коэффициент корреляции и ковариация.
Коэффициентом корреляции называется
p(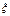 1,
1, 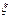 2)=
2)=  Свойства1.
Свойства1.  2. если
2. если  1 и
1 и  2 независимы, то коэффициент корреляции равен 0. Обратное не верно. Если p=0, то говорят, что
2 независимы, то коэффициент корреляции равен 0. Обратное не верно. Если p=0, то говорят, что  1 и
1 и  2 некоррелированы.
3.если
2 некоррелированы.
3.если  1 и
1 и  2 связаны линейной функциональной зависимостью, то в этом случае p(
2 связаны линейной функциональной зависимостью, то в этом случае p( 1,
1,  2)=1
Если
2)=1
Если 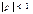 , то говорят, что
, то говорят, что  1 и
1 и  2 связаны корреляционной зависимостью, тем более тесной, чем ближе
2 связаны корреляционной зависимостью, тем более тесной, чем ближе  к 1.
Коэффициент корреляции служит для количественной характеристики зависимости между случайными величинами.
Если
к 1.
Коэффициент корреляции служит для количественной характеристики зависимости между случайными величинами.
Если 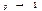 , то говорят, что зависимость близка к линейной.
Ковариацией случайных величин
Cov(
, то говорят, что зависимость близка к линейной.
Ковариацией случайных величин
Cov( 1,
1,  2)=M((
2)=M(( 1-M
1-M  1)(
1)( 2-M
2-M  2))
Называется произведение отклонений случайных величин от своего МО.
Свойства ковариации
1. cov(
2))
Называется произведение отклонений случайных величин от своего МО.
Свойства ковариации
1. cov( 1,
1,  1)=M(
1)=M( 1-M
1-M  1)2=D
1)2=D  1
2. для независимых случайных величин коэффициент ковариации равен 0
cov (
1
2. для независимых случайных величин коэффициент ковариации равен 0
cov ( 1,
1,  2)=M
2)=M  1M
1M  2-M
2-M  1M
1M  2=0
Но обратное не верно. Т.е. можно привести пример, когда коэфф. ковариации равен 0, но случайные величины зависимы.
3.
2=0
Но обратное не верно. Т.е. можно привести пример, когда коэфф. ковариации равен 0, но случайные величины зависимы.
3.  4. cov (C
4. cov (C  1,
1,  2)=C cov (
2)=C cov ( 1,
1,  2)
Ковариация является качественной характеристикой зависимости случайных величин.
14. Моменты.
Математическое ожидание и дисперсия являются частными случаями моментов случайных величин. Начальным моментом порядка k с.в. Х называется м.о. k-й степени этой величины, обозначается через α k. α k = м (Хk ) Для д. с. в. начальный момент выражается суммой: α k =∑ х ik * pi, а для непрерывной случайной величины - интегралом α k =∫ х k * f (х) dх. В частности, α 1 = МХ, т. е. начальный момент 1- го порядка есть м. о. Центральным моментом порядка k с.в. Х называется м. о. величины (М – МХ)k, обозначается через µ k. µ k = М(Х – МХ)k В частности, µ 2 = DХ, т.е. центральный момент 2-го порядка есть дисперсия; µ 1 = М(Х – МХ) =0
Для д.с.в. µ k =∑ (хi – МХ)k * pi, а для н.с.в. µ k = ∫ (х- МХ)k * f (х) dх. Центральные моменты могут быть выражены через начальные моменты. Так, µ k =DХ = α 2 - α 12 Среди моментов высших порядков – 3-й и 4-й порядок. Коэффициентом асимметрии (скошенности) А с.в. Х наз. величина:
А= µ 3 /σх3 =М(Х-МХ)3 / (DХ)3/2 . Если А>0, то кривая распределения более полога справа от М0Х. Если А<0, то кривая распределения более полога слева от М0Х. Коэффициентом эксцесса (островершинности) Е с.в. Х наз. величина Е= (µ 4 /σх4 )-3 =М(Х-МХ)4 / (DХ)2 -3. Если Е>0 – более островершинное распределение, а распределения плосковершинные имеют Е<0.
20. Независимость случайных величин
Случайные величины
2)
Ковариация является качественной характеристикой зависимости случайных величин.
14. Моменты.
Математическое ожидание и дисперсия являются частными случаями моментов случайных величин. Начальным моментом порядка k с.в. Х называется м.о. k-й степени этой величины, обозначается через α k. α k = м (Хk ) Для д. с. в. начальный момент выражается суммой: α k =∑ х ik * pi, а для непрерывной случайной величины - интегралом α k =∫ х k * f (х) dх. В частности, α 1 = МХ, т. е. начальный момент 1- го порядка есть м. о. Центральным моментом порядка k с.в. Х называется м. о. величины (М – МХ)k, обозначается через µ k. µ k = М(Х – МХ)k В частности, µ 2 = DХ, т.е. центральный момент 2-го порядка есть дисперсия; µ 1 = М(Х – МХ) =0
Для д.с.в. µ k =∑ (хi – МХ)k * pi, а для н.с.в. µ k = ∫ (х- МХ)k * f (х) dх. Центральные моменты могут быть выражены через начальные моменты. Так, µ k =DХ = α 2 - α 12 Среди моментов высших порядков – 3-й и 4-й порядок. Коэффициентом асимметрии (скошенности) А с.в. Х наз. величина:
А= µ 3 /σх3 =М(Х-МХ)3 / (DХ)3/2 . Если А>0, то кривая распределения более полога справа от М0Х. Если А<0, то кривая распределения более полога слева от М0Х. Коэффициентом эксцесса (островершинности) Е с.в. Х наз. величина Е= (µ 4 /σх4 )-3 =М(Х-МХ)4 / (DХ)2 -3. Если Е>0 – более островершинное распределение, а распределения плосковершинные имеют Е<0.
20. Независимость случайных величин
Случайные величины  1,
1,  2 называются независимыми, если для любых действительных чисел x1,…,xn
2 называются независимыми, если для любых действительных чисел x1,…,xn 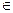 R случайные события (
R случайные события ( 1<X1),…, (
1<X1),…, ( n<Xn) независимы.
Из определения независимых событий вероятность появления должна равняться произведению вероятностей
P(
n<Xn) независимы.
Из определения независимых событий вероятность появления должна равняться произведению вероятностей
P( 1<X1,…,
1<X1,…,  n<Xn )=P(
n<Xn )=P( 1<X1)…P(
1<X1)…P( n<Xn)
Случайные события независимы, если многомерная функция распределения равна произведению многомерных.
1. Дискретные случайные величины
n<Xn)
Случайные события независимы, если многомерная функция распределения равна произведению многомерных.
1. Дискретные случайные величины  будут независимы, если.
будут независимы, если. 
 для всех,
для всех,  2. Непрерывные случайные величины
p(x,y)=
2. Непрерывные случайные величины
p(x,y)=  Если случайные величины независимы, то
Если случайные величины независимы, то  .
23.Теорема Чебышева. Теорема Бернулли.
Теорема Чебышева:Если X1, X2,…,Xn – последовательность независимых случайных величин, имеющих конечные дисперсии, ограниченные одним и тем же числом С, то для любого ε >0 выполняется
.
23.Теорема Чебышева. Теорема Бернулли.
Теорема Чебышева:Если X1, X2,…,Xn – последовательность независимых случайных величин, имеющих конечные дисперсии, ограниченные одним и тем же числом С, то для любого ε >0 выполняется
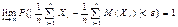 Доказательство.
Введем в рассмотрение случайную величину – среднее арифметическое случайных величин
Доказательство.
Введем в рассмотрение случайную величину – среднее арифметическое случайных величин
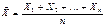 Найдем матожидание
Найдем матожидание 
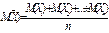 И дисперсию
И дисперсию 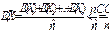 Следовательно – дисперсия конечная. Тогда к
Следовательно – дисперсия конечная. Тогда к 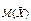 применим неравенство Чебышева
применим неравенство Чебышева  Переходя к пределу получим
Переходя к пределу получим 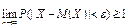 А так как вероятность не может быть больше 1, то предел равен 1.
А так как вероятность не может быть больше 1, то предел равен 1. 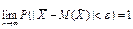 Суть закона больших чисел.Если число случайных величин неограниченно растет, то их среднее арифметическое утрачивает смысл случайной величины и стремится к постоянному числу равному среднему арифметическому их матожиданий.
Этот результат дает обоснование для теории ошибок. Следствием теоремы Чебышева является теорема Бернулли.
Пусть
Суть закона больших чисел.Если число случайных величин неограниченно растет, то их среднее арифметическое утрачивает смысл случайной величины и стремится к постоянному числу равному среднему арифметическому их матожиданий.
Этот результат дает обоснование для теории ошибок. Следствием теоремы Чебышева является теорема Бернулли.
Пусть 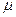 - число появления события А в n испытаниях в схеме Бернулли, и p – вероятность появления А в одном испытании. Тогда для любого
- число появления события А в n испытаниях в схеме Бернулли, и p – вероятность появления А в одном испытании. Тогда для любого  справедливо
справедливо 
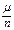 -частота появления события.Пусть
-частота появления события.Пусть 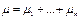 , где
, где  - число появления события А в i-ом испытании.Дисперсия любой величины
- число появления события А в i-ом испытании.Дисперсия любой величины  равна произведению pq, так как p+q=1, то p*q не превышает ¼, и следовательно дисперсии всех величин ограничены числом c=1/4
Применим теорему Чебышева:
равна произведению pq, так как p+q=1, то p*q не превышает ¼, и следовательно дисперсии всех величин ограничены числом c=1/4
Применим теорему Чебышева:
 так как матожидание равно вероятности наступления события.
Так как
так как матожидание равно вероятности наступления события.
Так как 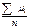 равна относительной частоте появления события А (m/n)(каждая величина
равна относительной частоте появления события А (m/n)(каждая величина 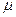 1,
1, 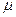 2,
2, 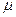 n при появлении события в соответствующем испытании равна 1 и поэтому их суму равна m), то окончательно получим
n при появлении события в соответствующем испытании равна 1 и поэтому их суму равна m), то окончательно получим  , что и т.д.
28. Числовые характеристики выборки.Опр1 Выборочным средним называется среднее арифметическое значение вариант
, что и т.д.
28. Числовые характеристики выборки.Опр1 Выборочным средним называется среднее арифметическое значение вариант  . Выборочной дисперсией называется среднее значение квадратов отклонения вариант от среднего.
. Выборочной дисперсией называется среднее значение квадратов отклонения вариант от среднего.  Если раскрыть скобки, получим еще одну формулу для вычисления дисперсии
Если раскрыть скобки, получим еще одну формулу для вычисления дисперсии 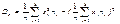 или
или 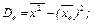 Выборочным средним квадратическим отклонением называется корень квадратный из дисперсии
Выборочным средним квадратическим отклонением называется корень квадратный из дисперсии  . Опр4. Размах варьирования
. Опр4. Размах варьирования 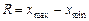 . Опр5. Начальным моментом r-го порядка называется среднее значение r-ых степеней вариант
. Опр5. Начальным моментом r-го порядка называется среднее значение r-ых степеней вариант  . Опр6. Центральным моментом r-го порядка называется среднее значение отклонений в степени r от среднего
. Опр6. Центральным моментом r-го порядка называется среднее значение отклонений в степени r от среднего 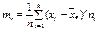 . Асиметрией называют величину равную
. Асиметрией называют величину равную 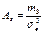 .
Пределы значений асимметрии от
.
Пределы значений асимметрии от 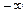 до
до  . При
. При  распределение симметрично, в частности для нормального распределения
распределение симметрично, в частности для нормального распределения  Эксцессом называют величину равную
Эксцессом называют величину равную 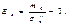 Эксцесс показывает степень крутости кривой распределения признака Х по сравнению с крутостью нормального распределения. Значения эксцесса лежат в полуинтервале
Эксцесс показывает степень крутости кривой распределения признака Х по сравнению с крутостью нормального распределения. Значения эксцесса лежат в полуинтервале 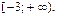 Для нормального распределения
Для нормального распределения 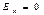 38. Вычисление теоретич.частот для норм.распр-ния.
Пусть имеется выборка (х1,х2,…хn) объема n, и есть основание предположить, что она имеет норм.распр-ние. Для вычисления теоретич.частот необх-мо выполнить след.действия:1. по данным выборки построить интерв.вариационный ряд. Для этого весь интервал наблюдаемых значений Х надо разделить на k частичных интервалов (хi,xi+1) одинаковой длины. Находим максим. и миним. значения выборки и размах варьирования: а=хmin,b=xmax R=b-a. Для определения количества интервалов группировки k воспользуемся формулой Стерджеса: k=3,32*lgn+1. Число k округляется в сторону наибольшего целого числа. Тогда ширину частичных интервалов (хi,xi+1) находим из формулы h=R/k. Интервалы строятся т.о., чтобы хmin и xmax входили внутрь интервалов. Для этого в качестве левой границы первого интервала можно взять число х0= хmin- h/2, а в качестве правой границы последнего интервала хk+1=xmax+h/2. В качестве частоты ni вариационного ряда записывают число наблюдений, попавших в каждый [xi,xi+1) промежуток.
2. для того, чтобы получить оценки параметров матем. ожидания, а и среднего квадратич. отклонения σ перейдем к дискретному ряду, взяв в качестве вариант ряда Х середины построенных интервалов xi*. В итоге получим последовательность равностоящих вариант и соответствующих им частот. Несмещенной оценкой матем.ожидания явл. выборочное среднее xВ, а дисперсии – исправленная выборочная дисперсия S2 .
а= xВ=1/n*∑ xi* ni, σ2= S2=1/n-1*∑ (xi*- xВ)2 ni или S2=(n/n-1)*Dв.
3. сделаем преобразование стандартизации для Х, перейдя к величинам zi= (xi- xВ)/S и zi+1=(xi+1- xВ)/S, i=0, k. Причем наименьшее значение z0 будем считать равным -∞, а наибольшее значение –zk+1=+∞, т.к. теоретическое норм.распр-ние принимает значения на всей числовой оси.
4. вычислим вероятности pi попадания Х в интервалы (zi, zi+1): pi=P(zi<x< zi+1)=Ф0(zi+1)- Ф0(zi), где i=0, k, Ф0(х)= -ф-ция Лапласа
5. рассчитаем теоретические частоты ni’=npi.Замечания
1.чтобы эмпирическая ф-ция распр-ния лучше описывала теоретическую, нужно, чтобы число интервалов было по возможности большим.
2.для выполнения предельного перехода к
распр-нию χ2 нужно, чтобы эмпирич. Частоты не были маленькими (ni>5). Если какой-то интервал содержит малые значения ni, то он объединяется с соседним интервалом, а их частоты складываются. Тогда число степеней свободы критерия χ2 уменьшается на единицу
43. Парный коэффициент корреляции.
38. Вычисление теоретич.частот для норм.распр-ния.
Пусть имеется выборка (х1,х2,…хn) объема n, и есть основание предположить, что она имеет норм.распр-ние. Для вычисления теоретич.частот необх-мо выполнить след.действия:1. по данным выборки построить интерв.вариационный ряд. Для этого весь интервал наблюдаемых значений Х надо разделить на k частичных интервалов (хi,xi+1) одинаковой длины. Находим максим. и миним. значения выборки и размах варьирования: а=хmin,b=xmax R=b-a. Для определения количества интервалов группировки k воспользуемся формулой Стерджеса: k=3,32*lgn+1. Число k округляется в сторону наибольшего целого числа. Тогда ширину частичных интервалов (хi,xi+1) находим из формулы h=R/k. Интервалы строятся т.о., чтобы хmin и xmax входили внутрь интервалов. Для этого в качестве левой границы первого интервала можно взять число х0= хmin- h/2, а в качестве правой границы последнего интервала хk+1=xmax+h/2. В качестве частоты ni вариационного ряда записывают число наблюдений, попавших в каждый [xi,xi+1) промежуток.
2. для того, чтобы получить оценки параметров матем. ожидания, а и среднего квадратич. отклонения σ перейдем к дискретному ряду, взяв в качестве вариант ряда Х середины построенных интервалов xi*. В итоге получим последовательность равностоящих вариант и соответствующих им частот. Несмещенной оценкой матем.ожидания явл. выборочное среднее xВ, а дисперсии – исправленная выборочная дисперсия S2 .
а= xВ=1/n*∑ xi* ni, σ2= S2=1/n-1*∑ (xi*- xВ)2 ni или S2=(n/n-1)*Dв.
3. сделаем преобразование стандартизации для Х, перейдя к величинам zi= (xi- xВ)/S и zi+1=(xi+1- xВ)/S, i=0, k. Причем наименьшее значение z0 будем считать равным -∞, а наибольшее значение –zk+1=+∞, т.к. теоретическое норм.распр-ние принимает значения на всей числовой оси.
4. вычислим вероятности pi попадания Х в интервалы (zi, zi+1): pi=P(zi<x< zi+1)=Ф0(zi+1)- Ф0(zi), где i=0, k, Ф0(х)= -ф-ция Лапласа
5. рассчитаем теоретические частоты ni’=npi.Замечания
1.чтобы эмпирическая ф-ция распр-ния лучше описывала теоретическую, нужно, чтобы число интервалов было по возможности большим.
2.для выполнения предельного перехода к
распр-нию χ2 нужно, чтобы эмпирич. Частоты не были маленькими (ni>5). Если какой-то интервал содержит малые значения ni, то он объединяется с соседним интервалом, а их частоты складываются. Тогда число степеней свободы критерия χ2 уменьшается на единицу
43. Парный коэффициент корреляции.

 Коэффициент обладает все теми же свойствами, что и теоретический коэффициент корреляции.
1.если x и y независимы, то
Коэффициент обладает все теми же свойствами, что и теоретический коэффициент корреляции.
1.если x и y независимы, то 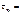 0.
2. -1<=
0.
2. -1<= 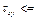 1
3.если x и y связаны линейной зависимостью, т.е. при
1
3.если x и y связаны линейной зависимостью, т.е. при 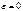 , то
, то
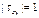 b>0,
b>0,  =1
b<0,
=1
b<0,  =-1
Таким образом коэффициент является количественной характеристикой зависимости x и y. Чем ближе
=-1
Таким образом коэффициент является количественной характеристикой зависимости x и y. Чем ближе  к единице, тем теснее и ближе к линейной зависимости между X и Y.
37. Критерий согласия Пирсона.
Критерий проверки гипотез о предполагаемом виде распределения называется критерием согласия. Наиболее распространенным из них является критерий согласия Пирсона или критерий
к единице, тем теснее и ближе к линейной зависимости между X и Y.
37. Критерий согласия Пирсона.
Критерий проверки гипотез о предполагаемом виде распределения называется критерием согласия. Наиболее распространенным из них является критерий согласия Пирсона или критерий  .В наиболее часто используемом на практике критерии χ 2 - Пирсона в качестве меры расхождения U,берется величина χ 2 , равная сумме квадратов отклонений частостей. ωi от гипотетических (предполагаемых) pi, рассчитанных по предполагаемому распределению, взятых с некоторыми весами сi: U= χ 2=∑ сi (ωi-pi)2 . взяв в качестве весов сi =n/pi, можно доказать, что при n →∞ статистика U= χ 2=∑ n/pi (ωi-pi)2 или U= χ 2=∑(n1 - npi)2 / npi (*). Для принятия или непринятия гипотезы находим статистику χ 2 - мера расхождения между опытными данными (в вариационном ряду) и теоретическими данными (по графику). Ni – частоты вариационного ряда, pi – вероятность, найденная в предположении, что СВ подчинена опред. Норм. Закону. Схема применения: 1. определите меру расхождения эмпирических и теоретических частот χ 2 по (*).2. для выбранного уровня значимости α по таблице χ 2 - распределения находят критическое значение χ 2 α;к при числе степеней свободы к=m-r-1. 3. если наблюдаемое значение χ 2 больше критического, то гипотеза отвергается. Если меньше, то принимается.
.В наиболее часто используемом на практике критерии χ 2 - Пирсона в качестве меры расхождения U,берется величина χ 2 , равная сумме квадратов отклонений частостей. ωi от гипотетических (предполагаемых) pi, рассчитанных по предполагаемому распределению, взятых с некоторыми весами сi: U= χ 2=∑ сi (ωi-pi)2 . взяв в качестве весов сi =n/pi, можно доказать, что при n →∞ статистика U= χ 2=∑ n/pi (ωi-pi)2 или U= χ 2=∑(n1 - npi)2 / npi (*). Для принятия или непринятия гипотезы находим статистику χ 2 - мера расхождения между опытными данными (в вариационном ряду) и теоретическими данными (по графику). Ni – частоты вариационного ряда, pi – вероятность, найденная в предположении, что СВ подчинена опред. Норм. Закону. Схема применения: 1. определите меру расхождения эмпирических и теоретических частот χ 2 по (*).2. для выбранного уровня значимости α по таблице χ 2 - распределения находят критическое значение χ 2 α;к при числе степеней свободы к=m-r-1. 3. если наблюдаемое значение χ 2 больше критического, то гипотеза отвергается. Если меньше, то принимается.
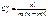 3. Сочетанием называется комбинации, состоящие из n элементов по m, которые различаются только составом элементов. Число сочетаний из n элементов по m вычисляется по формуле:
3. Сочетанием называется комбинации, состоящие из n элементов по m, которые различаются только составом элементов. Число сочетаний из n элементов по m вычисляется по формуле:
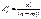 Свойство сочетаний.
1. Cn0=1, 0!=1
2. Cn1= n,
3. Cnm=Cnn-m
Гипергеометрическоераспределение
Урновая схема:
Пусть в урне имеется N шаров, среди которых М белых, а остальные черные. Наудачу вытащили k шаров, найти вероятность того, что среди них l белых.
Свойство сочетаний.
1. Cn0=1, 0!=1
2. Cn1= n,
3. Cnm=Cnn-m
Гипергеометрическоераспределение
Урновая схема:
Пусть в урне имеется N шаров, среди которых М белых, а остальные черные. Наудачу вытащили k шаров, найти вероятность того, что среди них l белых.
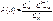 Эта ф-ла наз. гипергеометрическим распределением
6. Формула полной вероятности. Формула Байеса.
Пусть событие А может произойти только с одним из n несовместных событий H1…Hn, образующих полную группу:
Эта ф-ла наз. гипергеометрическим распределением
6. Формула полной вероятности. Формула Байеса.
Пусть событие А может произойти только с одним из n несовместных событий H1…Hn, образующих полную группу:
 Ø,
Ø, 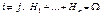 , тогда
, тогда 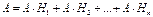 .Так как события
.Так как события 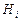 и
и  несовместны, то и (
несовместны, то и (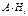 ) и
(
) и
( ) являются несовместными. Тогда по теореме сложения
) являются несовместными. Тогда по теореме сложения 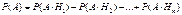 .Применяя теорему умножения к каждому слагаемому, получим формулу полной вероятности:
.Применяя теорему умножения к каждому слагаемому, получим формулу полной вероятности: 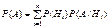 .События H1, H2,…, Hn часто называют гипотезами.Иногда интересует, как перераспределятся вероятности гипотез после того, как событие А уже произошло:
.События H1, H2,…, Hn часто называют гипотезами.Иногда интересует, как перераспределятся вероятности гипотез после того, как событие А уже произошло: 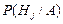 . По теореме умножения
. По теореме умножения 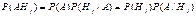 ,
,  .Подставляя в знаменатель формулу полной вероятности, получим формулу Байеса:
.Подставляя в знаменатель формулу полной вероятности, получим формулу Байеса:  .
10. Плотность распределения вероятностей и ее свойства. Плотностью распределения вероятностей случайной величины
.
10. Плотность распределения вероятностей и ее свойства. Плотностью распределения вероятностей случайной величины  называется производная функции распределения:
называется производная функции распределения: 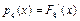 .Свойства.1.
.Свойства.1. 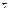
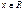 ,
, 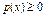 , так как это производная неубывающей функции2.
, так как это производная неубывающей функции2.  , т.к.
, т.к.  3.
3. 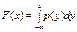 .
Следует из определения и свойства 2.
4. Свойство нормировки:
.
Следует из определения и свойства 2.
4. Свойство нормировки:  .В частности, если все возможные значения случайной величины заключены в интервале от a до b, то
.В частности, если все возможные значения случайной величины заключены в интервале от a до b, то 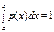 .Случайная величина называется распределенной по равномерному закону, если ее плотность вероятности принимает постоянное значение в пределах заданного интервала.
.Случайная величина называется распределенной по равномерному закону, если ее плотность вероятности принимает постоянное значение в пределах заданного интервала. 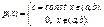
Определение 10.1. Математическим ожиданием дискретнойслучайной величины с законом распределения (xi, pi) называется сумма ряда
 , если этот ряд сходится абсолютно.
, если этот ряд сходится абсолютно.
Замечание: Если математическое ожидание равно бесконечности, то говорят, что оно не существует.
Если не все вероятности в некотором примере равны, то 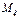 характеризует среднее значение взвешенное по вероятности.
характеризует среднее значение взвешенное по вероятности.
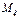 непрерывной случайной величины с плотностью вероятности р(х) называется интеграл
непрерывной случайной величины с плотностью вероятности р(х) называется интеграл 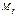 =
= 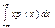 Свойства математического ожидания.
Свойства математического ожидания.
1. 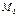 С=С
С=С
2. 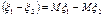
3. Для независимых случайных величин событий  и
и  мат ожидание произведения равно произведению матожиданий
мат ожидание произведения равно произведению матожиданий
M(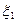 *
* 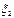 )=M
)=M 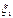 *M
*M 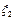
Следовательно
M(a 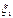 )=a M
)=a M 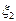
|
|
|
|
|
Дата добавления: 2015-03-31; Просмотров: 601; Нарушение авторских прав?; Мы поможем в написании вашей работы!