Примеры задач, решаемых методом динамического программирования

1) Задача о распределении средств

Планируется распределить начальную сумму средств S₀ между n-предприятиями P₁…P_n.

Предполагается, что выделенные предприятию P_i в начале планового периода средства x_i приносят доходы f_i(x_i).

Определить, какое количество средств можно выделить на каждое предприятие, чтобы сумма дохода была max?

Мат.модель:

x_i – количество средств

f – сумма доходов от вложений

x₁ + … + x_n = S₀, x_i ≥ 0

S_i-1 – сумма остаточных средств к (i+1)-шагу

S_i = S_i-1-x_i – уравнение состояний.

W_i(S_i-1) = max {f_i(S_i-1,U_i) + W_i+1(S_i)}

W_n(S_n-1) = max {f_n(S_n-1,U_n)}

2) Задача о замене оборудования

Оптимальной стратегией в данной задаче является нахождение оптимальных сроков замены оборудования. В качестве критерия оптимальности выступает либо прибыли, полученная от эксплуатации, либо затраты.

Будем предполагать, что решение о замене оборудования или сохранения, принимается в начале каждого промежутка времени, на который разбит весь плановый период.

Основной характеристикой оборудования будем считать его возраст.

Мат.модель:

f(t) – стоимость произведенной продукции на оборудовании в течении n-лет.

P_i – начальная стоимость оборудования.

R_i(t) – ежегодные затраты на эксплутацию оборудования.

φ(t) – ликвидная стоимость оборудования

S_i = t+1 (если U_i = U^{сохранить} ₎ или 1 (если U_i = U^{заменить}₎ – уравнение состояний

f_i(S_i-1,U_i) = f(t) – R(t) (если U_i = U^{сохранить} ₎ или φ(t)-f(0)-P–R(0) (если U_i = U^{заменить}₎

Функциональное уравнение:

W_i(t) = max (f(t)-R(t)+W_i+1(t+1)) (если U_i = U^{сохранить} ₎ или φ(t)-f(0)-P–R(0) (если U_i = U^{заменить}₎

Задачи с мультипликативным критерием

До сих пор W – сумма выигрышей на каждом шаге. Такая форма называется аддитивной.

В некоторых задачах критерий представляет собой не сумму, а произведение на каждом шаге.

В этом случае уравнение запишется в виде W_i(S_i-1) = max {f_i(S_i-1,U_i) × W_i+1(S_i)}

3) Задача о распределении средств для повышения надежности тех.устройств

Имеется некоторое тех.устройство S, состоящее из m-элементов или узлов, соединенных последовательно.

Безотказная работа каждого элемента необходима для работы устройства S в целом.

Элементы могут отказывать не зависимо друг от друга.

Надежность всего устройства = произведению надежности всех элементов.

В распоряжении имеется некоторые средства S₀, которые можно употребить на повышение надежности элемента.

x_i – количество средств, выделенных для повышения надежности

S_i+1 – количество оставшихся средств к i-шагу

S_i-1-S_i = S

P_i(S_i-1) – условие max надежности

Функциональное уравнение:

P_i(S_i-1) = max f_i(x_i)P_i+1(S_i)

P_m(S_m-1)=max f_m(x_m)

4) Задача о назначении

Предположим, что для выполнения m-различных работ требуется распределить n-работников, причем, каждый работник может выполнять только одну работу и каждая работа может быть выполнена только одним работником.

Выполнение i-работ (1≤ i ≤ m) j-работником (1 ≤ j ≤ n) связана с затратами времени, определенных его квалификацией – с_i,j

Задача состоит в таком распределении исполнении работ, чтобы сумма затраты времени была минимальной.

m=n

Мат.модель:

x_ij = 1 (если i-работу выполняет j-работник) или 0

f=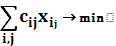

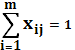
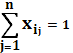, x_ij – целые, не отрицательные

Дата добавления: 2015-04-23