Выпуклое и квадратичное программирование

Нелинейное программирование

Постановка задачи:

min f (x) = g_i(x_i) ≤ (=) b_i

i = 1÷ m

Задача оптимизации является задачей нелинейного программирования, если хотя бы одна из функций f(x), g₁(x)…g_n(x) – является нелинейной.

В отличие от задач линейного программирования, решение задач нелинейного программирования может достигаться в любой точке ОДЗ, поэтому и не существует алгоритма, который позволил бы решить любую задачу нелинейного программирования, т.к. невозможно перебрать все точки.

Кроме того, т.к. нелинейная функция может иметь как локальные, так и глобальные экстремумы, то только в случае задачи выпуклого программирования можно гарантировать, что найденное решение является глобальным.

Если задача нелинейного программирования содержит 2 переменных, то она решается графически.

Если в задаче нелинейного программирования ограничения – равенства, а f(x), g₁(x)…g_n(x) – непрерывно дифференцируемы, то задача решается с помощью метода множителей Лагранжа.

Решение задач выпуклого программирования (З.В.П.)

Постановка задачи:

min f (x), при g_i(x_j) ≤ b_i, i = 1÷ m

x_j ≥ 0, j = 1÷ n

f(x), g₁(x)…g_n(x) – выпуклые вниз функции.

Для решения данной задачи составим функция Лагранжа:

L (x, λ) = f(x) + ))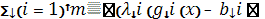

x = (x₁…x_n), λ = (λ₁…λ_n)

Совокупность векторов {x^*, λ^*} (где x^* ≥0, λ^* ≥0) называется седловой точкой функции Лагранжа, если для любых х из ОДЗ и для любых λ выполняется условие:

L (x^*, λ) ≤ L (x^*, λ^*) ≤ L (x, λ^*)

Теорема Куна-Такера:

Если x^*, λ^* - седловая точка функции Лагранжа, то x^*- оптимальное решение З.В.П.

Теорема Куна-Такера для частных случаев:

З.В.П. для min f(x):

g_i(x_j) ≤ bi, i = 1÷ m

x_j ≥ 0, j = 1÷ n

Тогда условие Куна-Такера можно записать аналитически

Пусть x^*, λ^* - седловая точка

Произведение j-переменной на соответствующую переменную в седловой точке = 0.

x_j^* _×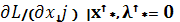

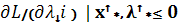
Произведение i-переменной на соответствующую переменную в седловой точке = 0.

λ_i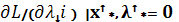^* _× , λ_i ≥ 0

З.В.П. для max f(x):

L (x, λ) = f(x) + ),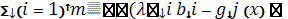

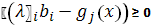
Тогда условие Куна-Такера можно записать аналитически

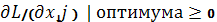
x_j^* _×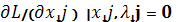

λ_i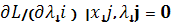^* _× , λ_i ≥ 0

Решение задач квадратичного программирования (З.К.П.)

(частный случай задачи нелинейного программирования)

Постановка задачи:

min f(x) =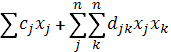

Ограничения:

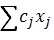≤ b_i, i = 1 ÷ m

x_j ≥ 0, j = 1 ÷ n

F(x) = 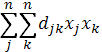– квадратичная форма

F(x) называется положительно (отрицательно) определенной, если для любого х ≠ 0: (пол) F(x) > 0, (отр) F(x) < 0 и F(0) = 0.

F(x) называется положительно (отрицательно) полуопределенной, если для любого х: (пол) F(x) ≥ 0, (отр) F(x) ≤ 0 и найдется такой х ≠ 0, что F(x) = 0.

Если квадратичная форма принимает как положительные, так и отрицательные значения, то она называется неопределенной.

Утверждение:

Квадратичная форма F(x) – выпуклая вниз (вверх), тогда и только тогда, когда она положительно (отрицательно) полуопределена, и строго выпуклая вниз (вверх), тогда и только тогда, когда она положительно (отрицательна) определена.

Критерии:

1) F(x) – положительно определена тогда и только тогда, когда все |∆| (миноры) являются положительными.

2) F(x) - положительно полуопределена тогда и только тогда, когда все |∆_r| (главные миноры) > 0, а |∆_r+1| = 0.

3) F(x) – отрицательно определена тогда и только тогда, когда все |∆| в знаках чередуются.

4) F(x) – отрицательно полуопределена тогда и только тогда, когда все |∆_r| в знаках чередуются, а с |∆_r+1| = 0.

Дата добавления: 2015-04-23