Построение моделей ЛП простейших экономических задач

Линейное программирование

Линейное программирование – раздел математического программирования, в котором рассматриваются задачи нахождения экстремума минимума функции, когда на переменные наложены линейные ограничения.

Постановка задачи:

min f(x) = c₁x₁+c₂x₂+ … + c_nx_n

При ограничениях

a₁₁x₁+a₁₂x₂+ … + a_1nx_n = b₁

a₂₁x₁+a₂₂x₂+ … + a_2nx_n = b₂

…

a_m1x₁+a_m2x₂+ … + a_mnx_n = b_m

x_i ≥ 0, m = 1 ÷ n

Рассмотрим вопрос о существовании допустимого решения.

Теорема Кронакера-Коппеля:

Для того, чтобы система линейных уравнений была совместима, необходимо и достаточно, чтобы ранг матрицы А совпадал с рангом расширенной матрицы.

В дальнейшем будем предполагать, что условия совместимости выполняются.

Случай № 1.

Ранг матрицы А равен количеству переменных (r(A) = n).

Тогда, отбросив линейную зависимость, уравнения приведем к системе вида:

a₁₁x₁+a₁₂x₂+ … + a_1nx_n = b₁

…

a_m1x₁+a_m2x₂+ … + a_mnx_n = b_m

r (A) = n => Определитель матрицы (∆) ≠ 0

Система имеет единственное решение по теореме Крамера и это решение вида x_i = ∆_i / ∆

Если в полученном решении все переменные x_i ≥ 0, то это решение является и допустимым и оптимальным.

Случай № 2.

Ранг матрицы А меньше количества переменных (r(A) < n).

Это означает, что в матрице А найдется ∆_r ≠ 0, значит, r – переменных можно единственным образом выразить через (n - r) -переменных.

х_i = β_i + α_{1, r+1} x_r+1 + … + α_1nx_n

…

х_r = β_r + α_{r, r+1} x_r+1 + … + α_rnx_n

Переменные x_r+1...x_n могут принимать произвольные значения, потому они называются свободными.

Переменные x₁…x_r, которые выражаются через свободные переменные, называются базисными.

Если среди полученного множества решений системы найдутся решения с неотрицательными переменными, то эти решения и будут являться допустимыми для задачи линейного программирования.

Допустимым решением, в котором все свободные переменные равны 0, называют опорным.

Решение системы линейных уравнений, в котором все свободные переменные равны 0, называют базисным.

Опорные решения, которые содержат ровно r - положительных переменных, называют не вырожденным.

В противном случае, когда < r – решение вырожденное.

Формы записи З.Л.П.

1) Общая форма

Min (Max) f (x) =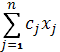

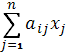≤ (=) b_i,

i = 1 ÷ m, c_j ≥ 0, j = 1÷ L, L ≤ m

2) Основная (каноническая)

Min f (x) =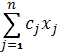

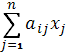= b_i, i= 1÷ m

x_j­ ≥ 0, j = 1÷ n

3) Стандартная

Min f (x) =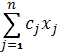

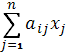≤ b_i, i= 1÷ m

j = 1÷ n

Преобразования З.Л.П.

1. Преобразование целевой функции: Задача max Z равносильна min (-Z).

2. Преобразование ограничений

А) неравенство в равенство:
введение неотрицательных переменных
Б) равенство в неравенство:
выразить базисные переменные через свободные и воспользоваться условием неотрицательности базисных переменных.

3. Преобразование переменных: Переменная, на которую не наложены условия неотрицательности может быть представлена как разность двух неотрицательных переменных.

Дата добавления: 2015-04-23