Методы решения задач линейного программирования

Графический метод

Графически З.Л.П. решается, когда 2 свободные переменные (n – m) = 2, где m = r(A).

Алгоритм:

1. Преобразовать ограничения (выразить базисные переменные через свободные и воспользоваться условием неотрицательности базисных переменных)

2. Выразить целевую функцию через свободные переменные

3. Построить область допустимых значений (ОДЗ)

4. Построить линию уровня

5. Определить оптимальное решение.

На основании графического способа решения З.Л.П. можно сделать следующие выводы:

1) Область допустимых значения в З.Л.П. может иметь следующий вид:

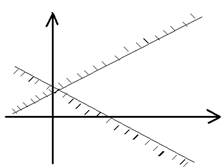
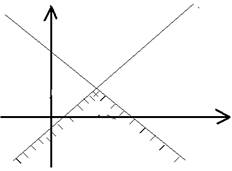
а) б) единственное решение

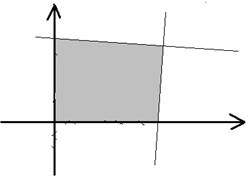
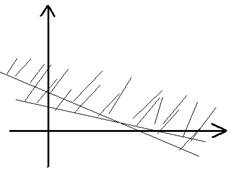
в) выпуклый многоугольник г) выпуклая неограниченная область

2) Задача линейного программирования может не иметь оптимального решения, может иметь множество решений и может иметь единственное решение.

3) З.Л.П. не имеет оптимального решения, когда область допустимого значения решений не ограничена в направлении градиента (max) или антиградиента (min).

4) Если З.Л.П. имеет оптимальное решение, то оно достигается в одной из угловых точек области допустимых значений.

5) Если оптимальное решение задачи линейного программирования достигается в 2х точках, то оно достигается в любой точке отрезка их соединяющих (случай альтернативного оптимума).

6) Решение, которое соответствует угловым точкам области допустимых решений, является опорным, т.к. по крайней мере 2 переменные в этой точке обращены в ноль.

Если в угловой точке больше 2х переменных обращаются в 0, то опорное решение является вырожденным. Геометрически это означает, что через эту точку проходит более 2х ограничений, т.е. в задаче есть избыточные условия.

7) Две смежные угловые точки области допустимых решений отличаются по одной переменной в составе базисных и свободных переменных.

Поэтому переход от одной точки к другой возможен за счет обмена между базисной и свободной переменной.

Симплекс-метод

Симплекс-метод представляет собой вычислительную процедуру, которая, начиная с произвольных угловых точек области допустимых решений, осуществляет переход от одной точки к другой смежной с предыдущей точкой в направлении возрастания f (max) или убывания f (min).

Переход осуществляется за счет обмена между базисными и свободными переменными.

Постановка задачи:

min f (x) = c₁x₁ + … + c_nx_n

Ограничения:

a₁₁x₁+a₁₂x₂+ … + a_1nx_n = b₁

…

a_m1x₁+a_m2x₂+ … + a_mnx_n = b_m

1. Табличный алгоритм решения:

Проверить на оптимальность оценочную строку:

А) если оценки свободных переменных отрицательны (нулевые), то решение оптимально;

Б) если найдется хотя бы один положительный столбец, который содержит хотя бы один положительный коэффициент, то найденное решение может быть улучшено;

В) если найдется положительная оценка свободной переменной, столбец которой не содержит ни одного положительного коэффициента, то оптимального решения не существует, т.к. функция f → -∞.

1. В качестве включаемой в базис переменной выберем, с наибольшей по модулю отрицательной (положительной) оценкой.

2. В качестве исключаемой из базиса переменной выберем первую, обращающуюся в ноль (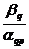), где q – разрешающая строка, p – разрешающий столбец.

3. Разделим элементы разрешающей строки на разрешающий элемент

4. Заполним базисные столбцы

5. Все остальные элементы пересчитать по формуле: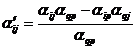

Методы искусственного базиса

М-метод или метод больших штрафов

Постановка задачи:

Min f (x) =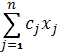

Ограничения:

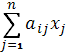= b_i, i= 1÷ m

x_j­ ≥ 0, j = 1÷ n

(!) Ограничения должны быть равенства.

Отличается от Симплекс-метода введением в ограничение задачи искусственные неотрицательные переменные y₁…y_n: 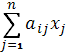+ y_i = b_i, b_i ≥0, i= 1÷ m.

За использование искусственных переменных на целевую функцию накладывается штраф T(x,y) = f(x) + M (y₁ + … + y_m), где M – очень большое положительное число.

В результате получаем новую задачу, которая называется М-задачей:

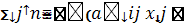+ y_i)= b_i

x_j, y_i ≥ 0

Выразим искусственные переменные y_i через системные ограничения и подставим их в функцию Т.

Тогда y₁…y_n – базисные переменные, а х₁…х_n – свободные.

М-задача решается обычным симплекс-методом.

Двухэтапный метод

Процесс нахождения оптимального решения разбит на 2 этапа:

1) Нахождение исходного опорного решения.

Для этого в ограничения задачи вводим искусственные переменные, так же как и в М-методе и составляем вспомогательную задачу min Т.

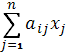+ y_i = b_i

x_j, y_i ≥ 0

Cоставляем min вспомогательную задачу суммы искусственных переменных при ограничениях.

Данная задача решается симплекс-методом (предварительно исключая искусственные переменные из функции Т).

Если min Т > 0, то исходное опорное решение не существует.

Если вспомогательная задача не разрешима, то не разрешима и исходная.

2) Нахождение оптимального решения.

Используем решение, найденное на 1 этапе: с помощью симплекс-метода находим оптимальное решение исходной задачи.

Дата добавления: 2015-04-23