
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные методы экологических исследований 13 страница
|
|
|
|
Решение.
Задача сводится к решению неравенства 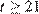 при заданных значениях начального напряжения на конденсаторе
при заданных значениях начального напряжения на конденсаторе  кВ, сопротивления резистора
кВ, сопротивления резистора  Ом и ёмкости конденсатора
Ом и ёмкости конденсатора  Ф:
Ф:
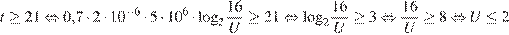 кВ.
кВ.
Ответ: 2.
13. B 13.  Объем прямоугольного параллелепипеда равен 60. Площадь одной его грани равна 12. Найдите ребро параллелепипеда, перпендикулярное этой грани.
Объем прямоугольного параллелепипеда равен 60. Площадь одной его грани равна 12. Найдите ребро параллелепипеда, перпендикулярное этой грани.
Решение.
Объем прямоугольного параллелепипеда равен  , где
, где 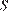 — площадь грани, а
— площадь грани, а  — высота перпендикулярного к ней ребра. Тогда
— высота перпендикулярного к ней ребра. Тогда
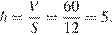
Ответ: 5.
14. B 14. Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение.
Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Средняя скорость автомобиля равна
 км/ч.
км/ч.
Ответ: 72.
15. B 15. Найдите наименьшее значение функции  на отрезке
на отрезке  .
.
Решение.
Найдем производную заданной функции:

Найдем нули производной на заданном отрезке:

Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:

В точке  заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:
заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:
 .
.
Ответ: −6.
16. C 1. а) Решите уравнение 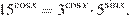
б) Найдите все корни этого уравнения, принадлежащие отрезку 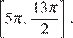
Решение.

а) Преобразуем исходное уравнение:

б) С помощью числовой окружности отберем корни, принадлежащие отрезку 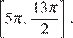 Получим числа:
Получим числа: 
Ответ: а)  б)
б) 
17. C 2. Длины ребер BC, BB 1 и BA прямоугольного параллелепипеда ABCDA 1 B 1 C 1 D 1равны соответственно 8, 12 и 9. Найдите расстояние от вершины D 1 до прямой A 1C.
Решение.
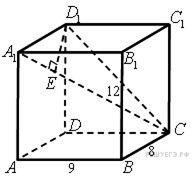 Опустим из точки D1 перпендикуляр D1E на прямую A1C. Так как
Опустим из точки D1 перпендикуляр D1E на прямую A1C. Так как 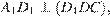 то
то  а, значит, отрезок D1E ― высота прямоугольного треугольника A1CD1, откуда
а, значит, отрезок D1E ― высота прямоугольного треугольника A1CD1, откуда 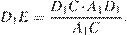 Далее находим:
Далее находим:

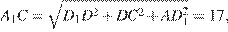

Ответ: 
18. C 3. Решите систему неравенств 
Решение.
1. Решим первое неравенство системы:

Пусть 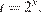 тогда неравенство примет вид:
тогда неравенство примет вид:  откуда
откуда
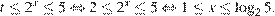
Решение первого неравенства исходной системы: 
2. Решим второе неравенство системы:

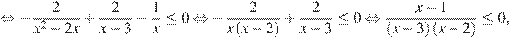 где
где 
Решение второго неравенства исходной системы: 
3. Поскольку 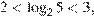 получаем решение исходной системы неравенств:
получаем решение исходной системы неравенств: 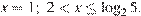
Ответ: 
19. C 4. Дан треугольник со сторонами 115, 115 и 184. Внутри него расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.
Решение.
 Рассмотрим равнобедренный треугольник
Рассмотрим равнобедренный треугольник 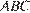 , в котором
, в котором 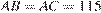 ,
, 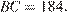 Пусть
Пусть  — высота треугольника
— высота треугольника 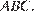 Тогда
Тогда 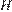 — середина
— середина 
Обозначим  Тогда
Тогда 
Предположим, что окружность радиуса  с центром
с центром 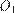 вписана в угол
вписана в угол 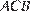 и касается основания
и касается основания 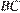 в точке
в точке  а окружность того же радиуса с центром
а окружность того же радиуса с центром  вписана в угол
вписана в угол 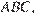 касается основания
касается основания  в точке
в точке  а первой окружности — в точке
а первой окружности — в точке 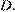 Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому
Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому
 а
а 
Из прямоугольного треугольника 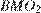 находим:
находим:
 Тогда
Тогда 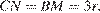
Линия центров касающихся окружностей проходит через точку их касания, поэтому 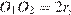 значит,
значит,  поскольку
поскольку  — прямоугольник. Следовательно,
— прямоугольник. Следовательно,
 откуда находим
откуда находим 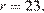
 Пусть теперь окружность радиуса
Пусть теперь окружность радиуса  с центром
с центром  вписана в угол
вписана в угол 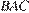 и касается боковой стороны
и касается боковой стороны 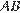 в точке
в точке 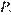 вторая окружность радиуса
вторая окружность радиуса  с центром
с центром  вписана в угол
вписана в угол 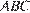 , касается боковой стороны
, касается боковой стороны  в точке
в точке  а также касается первой окружности.
а также касается первой окружности.
Из прямоугольных треугольников 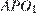 и
и  находим:
находим:
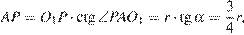

Следовательно,
 ,
,
откуда находим 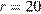 .
.
В случае, когда окружности вписаны в углы 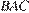 и
и  получим тот же результат.
получим тот же результат.
Ответ: 23 или 20.
20. C 5. Найдите все значения a, при каждом из которых уравнение
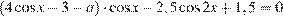
имеет хотя бы один корень.
Решение.

Запишем исходное уравнение в виде 
Пусть t = cos x, тогда исходное уравнение имеет хотя бы один корень, если уравнение 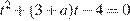 имеет хотя бы один корень, принадлежащий отрезку [−1; 1]. Графиком функции
имеет хотя бы один корень, принадлежащий отрезку [−1; 1]. Графиком функции  является парабола, ветви которой направлены вверх,
является парабола, ветви которой направлены вверх, 
следовательно, уравнение  имеет хотя бы один корень, принадлежащий отрезку [−1; 1], либо при условии
имеет хотя бы один корень, принадлежащий отрезку [−1; 1], либо при условии 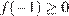 (рис. 1)
(рис. 1) 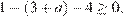 откуда
откуда  либо при условии
либо при условии 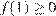 (рис. 2)
(рис. 2)  откуда
откуда 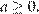
Ответ: 
21. C 6. Моток веревки режут без остатка на куски длиной не меньше 99 см, но не больше 102 см (назовем такие куски стандартными).
а) Некоторый моток веревки разрезали на 33 стандартных куска, среди которых есть куски разной длины. На какое наибольшее число стандартных одинаковых кусков можно было бы разрезать тот же моток веревки?
б) Найдите такое наименьшее число  , что любой моток веревки, длина которого больше
, что любой моток веревки, длина которого больше  см, можно разрезать на стандартные куски.
см, можно разрезать на стандартные куски.
Решение.
Решение каждого пункта состоит из двух частей: оценка и пример.
Рассмотрим моток веревки длиной  см. Условие того, что его можно разрезать на
см. Условие того, что его можно разрезать на  стандартных кусков, записывается в виде
стандартных кусков, записывается в виде 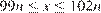 или
или 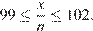
а) В данном случае имеем 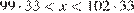 (неравенства строгие, поскольку среди кусков есть неравные). Пусть эту веревку можно разрезать на
(неравенства строгие, поскольку среди кусков есть неравные). Пусть эту веревку можно разрезать на 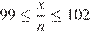 стандартных кусков, тогда При
стандартных кусков, тогда При 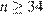 получаем
получаем
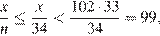
т.е. этот моток веревки нельзя разрезать больше, чем на 33 стандартных куска.
При  получаем
получаем 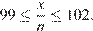 Значит, эту веревку можно разрезать на 33 одинаковых стандартных куска, но нельзя разрезать на большее количество стандартных кусков.
Значит, эту веревку можно разрезать на 33 одинаковых стандартных куска, но нельзя разрезать на большее количество стандартных кусков.
б) Отрезки 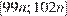 и
и  являющиеся решениями неравенств
являющиеся решениями неравенств 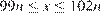 и
и 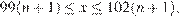 имеют общие точки для всех
имеют общие точки для всех 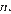 при которых
при которых 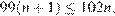 то есть при
то есть при 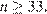 Значит, любую веревку длиной
Значит, любую веревку длиной 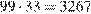 см или более можно разрезать на стандартные куски.
см или более можно разрезать на стандартные куски.
Докажем, что веревку, длина которой больше 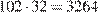 см, но меньше
см, но меньше 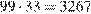 см, нельзя разрезать на
см, нельзя разрезать на  стандартных кусков ни для какого
стандартных кусков ни для какого  При
При 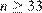 получаем
получаем  что противоречит условию
что противоречит условию 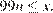 При
При 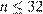 получаем
получаем 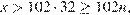 что противоречит условию
что противоречит условию  Таким образом, искомое число равно 3267.
Таким образом, искомое число равно 3267.
Ответ: а) 33; б) 3267.
Вариант № 17
Шоколадка стоит 40 рублей. В воскресенье в супермаркете действует специальное предложение: заплатив за две шоколадки, покупатель получает три (одну в подарок). Сколько шоколадок можно получить на 320 рублей в воскресенье?
Решение.
На 320 рублей можно купить 8 шоколадок по 40 рублей. Еще 4 будут даны в подарок. Всего можно будет получить 12 шоколадок.
Ответ: 12.
2. B 2. Железнодорожный билет для взрослого стоит 720 рублей. Стоимость билета для школьника составляет 50% от стоимости билета для взрослого. Группа состоит из 15 школьников и 2 взрослых. Сколько рублей стоят билеты на всю группу?
Решение.
Билет для ребенка стоит 720  0,5 = 360 руб. Стоимость билетов на 15 школьников и двух взрослых составляет
0,5 = 360 руб. Стоимость билетов на 15 школьников и двух взрослых составляет
360  15 + 720
15 + 720  2 = 5400 + 1440 = 6840 руб.
2 = 5400 + 1440 = 6840 руб.
Ответ: 6840.
3. B 3. На диаграмме показано количество посетителей сайта РИА Новости в течение каждого часа 8 декабря 2009 года. По горизонтали указывается номер часа, по вертикали — количество посетителей сайта за данный час. Определите по диаграмме разность наибольшего и наименьшего количества посетителей за час в данный день.
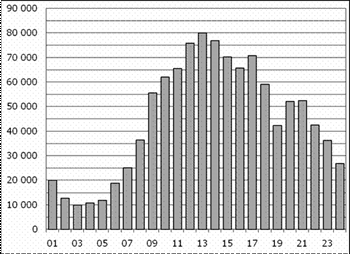
Решение.
Из диаграммы видно, что наибольшее и наименьшее количество посетителей составили 80 000 и 10 000 соответственно (см. рисунок). Их разность: 70 000 человек.
Ответ: 70 000.
4. B 4. Вася загружает на свой компьютер из Интернета файл размером 30 Мб за 28 секунд. Петя загружает файл размером 28 Мб за 24 секунды, а Миша загружает файл размером 38 Мб за 32 секунды. Сколько секунд будет загружаться файл размером 665 Мб на компьютер с наибольшей скоростью загрузки?
Решение.
Рассмотрим все случаи.
Скорость интернета Васи составляет 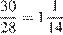 Мб/с.
Мб/с.
Скорость интернета Пети составляет 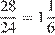 Мб/с.
Мб/с.
Скорость интернета Миши составляет 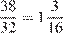 Мб/с.
Мб/с.
Поскольку 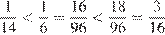 , с наибольшей скоростью может скачать файл Миша. На скачивание 665 Мб ему понадобится
, с наибольшей скоростью может скачать файл Миша. На скачивание 665 Мб ему понадобится
 с.
с.
Ответ: 560.
5. B 5.  Найдите высоту параллелограмма
Найдите высоту параллелограмма  , опущенную на сторону
, опущенную на сторону 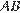 , если стороны квадратных клеток равны 1.
, если стороны квадратных клеток равны 1.
Решение.
 проведем высоту
проведем высоту  из вершины
из вершины 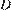 . По рисунку находим ее высоту.
. По рисунку находим ее высоту.
Ответ: 4.
6. B 6. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.
Решение.
Обозначим «1» ту сторону монеты, которая отвечает за выигрыш жребия «Физиком», другую сторону монеты обозначим «0». Тогда благоприятных комбинаций три: 110, 101, 011, а всего комбинаций 23 = 8: 000, 001, 010, 011, 100, 101, 110, 111. Тем самым, искомая вероятность равна:

Ответ: 0,375.
7. B 7. Найдите корень уравнения 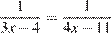 .
.
Решение.
Если две дроби с равным числителем равны, то равны их знаменатели. Имеем
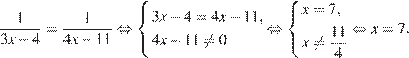
Ответ:7.
8. B 8. 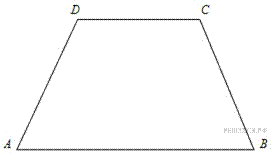 Основания равнобедренной трапеции равны 15 и 9, один из углов равен
Основания равнобедренной трапеции равны 15 и 9, один из углов равен  . Найдите высоту трапеции.
. Найдите высоту трапеции.
Решение.
 Проведем высоту
Проведем высоту  .
.
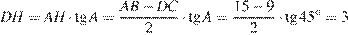 .
.
Ответ: 3.
9. B 9.  На рисунке изображен график функции f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых производная функции f(x) равна 0.
На рисунке изображен график функции f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых производная функции f(x) равна 0.
Решение.
Производная изображенной на рисунке функции f(x) равна нулю в точках экстремумов: −3,7; 1,4; 2,6 и 4,2. Производная равна нулю в 4 точках.
Ответ: 4.
10. B 10. 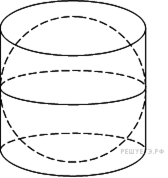
Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем шара.
Решение.
 ,
,
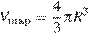
Выразим из формулы для объёма цилиндра 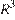 и подставим в формулу для объёма шара
и подставим в формулу для объёма шара
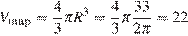
Ответ: 22.
11. B 11. Найдите значение выражения 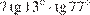 .
.
Решение.
Сходственные функции дополнительных углов равны. Поэтому
 .
.
Ответ: 7.
12. B 12. Мотоциклист, движущийся по городу со скоростью  км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением
км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением  км/ч
км/ч  . Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением
. Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением 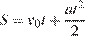 . Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.
. Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.
Решение.
Мотоциклист будет находиться в зоне функционирования сотовой связи, если 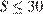 км. Задача сводится к нахождению наибольшего решения неравенства
км. Задача сводится к нахождению наибольшего решения неравенства 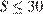 км при заданных значениях параметров
км при заданных значениях параметров  и
и  :
:
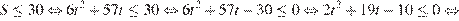

Учитывая то, что время – неотрицательная величина, получаем  ч, то есть
ч, то есть  мин.
мин.
Ответ: 30.
13. B 13.  Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.
Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.
Решение.
Объем прямоугольного параллелепипеда равен  , где
, где 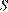 – площадь грани, а
– площадь грани, а  — высота перпендикулярного к ней ребра. Имеем
— высота перпендикулярного к ней ребра. Имеем
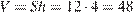 .
.
Ответ: 48.
14. B 14. Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
Решение.
Пусть масса 30-процентного раствора кислоты – 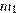 кг, а масса 60-процентного –
кг, а масса 60-процентного – 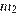 . Если смешать 30-процентный и 60-процентный растворы кислоты и добавить
. Если смешать 30-процентный и 60-процентный растворы кислоты и добавить 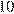 кг чистой воды, получится 36-процентный раствор кислоты:
кг чистой воды, получится 36-процентный раствор кислоты:  . Если бы вместо 10 кг воды добавили
. Если бы вместо 10 кг воды добавили 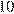 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты:
кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты:  . Решим полученную систему уравнений:
. Решим полученную систему уравнений:
|
|
|
|
|
Дата добавления: 2015-04-23; Просмотров: 918; Нарушение авторских прав?; Мы поможем в написании вашей работы!