
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные методы экологических исследований 11 страница
|
|
|
|
Решение.
Треугольник 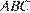 – так же равнобедренный, т.к. углы при основании
– так же равнобедренный, т.к. углы при основании  . Тогда радиус основания равен 6, и объем конуса, деленный на
. Тогда радиус основания равен 6, и объем конуса, деленный на  :
:
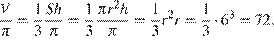
Ответ: 72.
14. B 14. Даша и Маша пропалывают грядку за 12 минут, а одна Маша — за 20 минут. За сколько минут пропалывает грядку одна Даша?
Решение.
За минуту Маша пропалывает одну двадцатую грядки, а Маша с Дашей вместе — одну двенадцатую. Поэтому за одну минуту Даша пропалывает  грядки. Всю грядку она прополет за 30 минут.
грядки. Всю грядку она прополет за 30 минут.
Ответ: 30.
15. B 15. Найдите точку максимума функции 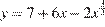 .
.
Решение.
Найдем производную заданной функции:
 .
.
Найдем нули производной:
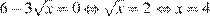 .
.
Определим знаки производной функции и изобразим на рисунке поведение функции:
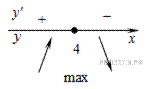
Искомая точка максимума  .
.
Ответ: 4.
16. C 1. а) Решите уравнение 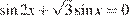 .
.
б) Найдите все корни этого уравнения, принадлежащие отрезку  .
.
Решение.
 а) Запишем уравнение в виде
а) Запишем уравнение в виде
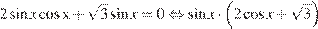 .
.
Значит, или  , откуда
, откуда  ,
, 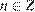 , или
, или 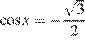 , откуда
, откуда 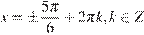 .
.
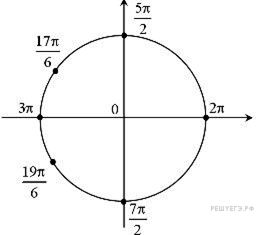
б) С помощью числовой окружности отберём корни, принадлежащие отрезку  . Получим числа:
. Получим числа: 
Ответ: а)  ,
, 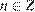 ;
; 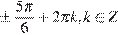 ; б)
; б) 
17. C 2. В правильной четырёхугольной призме  стороны основания равны
стороны основания равны  , а боковые рёбра равны
, а боковые рёбра равны  . На ребре
. На ребре  отмечена точка
отмечена точка 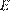 так, что
так, что 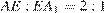 . Найдите угол между плоскостями
. Найдите угол между плоскостями  и
и 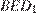 .
.
Решение.
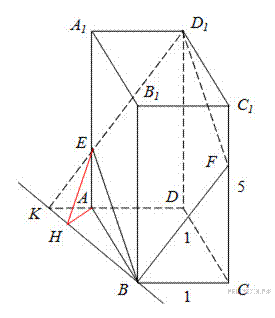 Прямая
Прямая  пересекает прямую
пересекает прямую  в точке
в точке  . Плоскости
. Плоскости 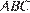 и
и  пересекаются по прямой
пересекаются по прямой 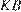 .
.
Из точки 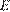 опустим перпендикуляр
опустим перпендикуляр 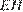 на прямую
на прямую 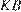 , тогда отрезок
, тогда отрезок  (проекция
(проекция 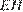 ) перпендикулярен прямой
) перпендикулярен прямой 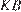 по теореме о трех перпендикулярах. Угол
по теореме о трех перпендикулярах. Угол 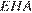 является линейным углом двугранного угла, образованного плоскостями
является линейным углом двугранного угла, образованного плоскостями 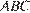 и
и  .
.
Поскольку 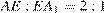 , получаем:
, получаем:
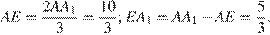
Из подобия треугольников  и
и  находим:
находим:
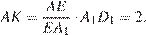
В прямоугольном треугольнике 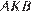 с прямым углом
с прямым углом 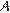 :
: 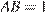 ,
,  ,
, 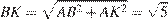 , откуда высота
, откуда высота
 .
.
Из прямоугольного треугольника 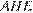 с прямым углом
с прямым углом 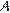 получаем:
получаем:
 .
.
Ответ:  .
.
18. C 3. Решите систему неравенств 
Решение.
1. Решим первое неравенство системы:

Рассмотрим два случая. Первый случай: 
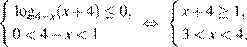 откуда
откуда 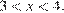
Второй случай: 
 откуда
откуда 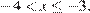
Решение первого неравенства исходной системы: 
2. Решим второе неравенство системы:

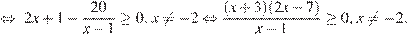
Решение второго неравенства исходной системы: 
3. Пересекая промежутки, получаем решение системы неравенств.
Ответ: 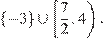
19. C 4. Прямая, перпендикулярная боковой стороне равнобедренного треугольника, отсекает от него четырёхугольник, в который можно вписать окружность. Найдите радиус окружности, если отрезок прямой, заключённый внутри треугольника, равен  , а отношение боковой стороны треугольника к его основанию равно
, а отношение боковой стороны треугольника к его основанию равно 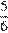 .
.
Решение.
Обозначим данный треугольник 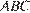 ,
,  — основание,
— основание, 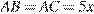 . Заметим, что окружность, о которой говорится в условии, — окружность, вписанная в треугольник
. Заметим, что окружность, о которой говорится в условии, — окружность, вписанная в треугольник 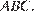 Пусть
Пусть 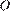 — её центр, а
— её центр, а 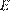 — точка касания с основанием
— точка касания с основанием 
Обозначим 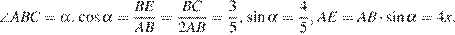
Так как 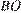 — биссектриса треугольника
— биссектриса треугольника  , то
, то 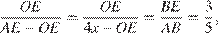 следовательно,
следовательно, 
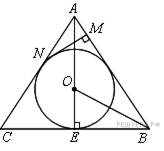
Рис. 1
Первый случай. Пусть прямая  перпендикулярная
перпендикулярная 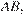 касается окружности, пересекает
касается окружности, пересекает  в точке
в точке 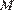 , а
, а  в точке
в точке  (рис. 1). Тогда
(рис. 1). Тогда  ,
, 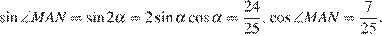
В треугольнике  имеем
имеем 
У описанного четырехугольника суммы противоположных сторон равны:
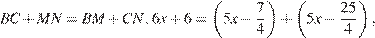
откуда находим: 
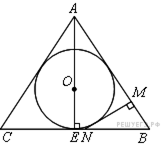
Рис. 2
Второй случай. Пусть прямая  перпендикулярная
перпендикулярная 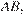 касается окружности, пересекает
касается окружности, пересекает  в точке
в точке 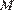 , а
, а  в точке
в точке 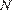 (рис. 2). В прямоугольном треугольнике
(рис. 2). В прямоугольном треугольнике 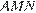 имеем
имеем 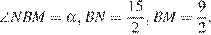
У описанного четырёхугольника  суммы противоположных сторон равны:
суммы противоположных сторон равны:
 ,
, 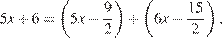
откуда находим: 
Ответ: 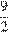 или
или 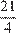 .
.
20. C 5. Найдите все значения a, при каждом из которых уравнение
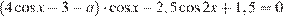
имеет хотя бы один корень.
Решение.

Запишем исходное уравнение в виде 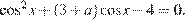
Пусть t = cos x, тогда исходное уравнение имеет хотя бы один корень, если уравнение 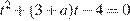 имеет хотя бы один корень, принадлежащий отрезку [−1; 1]. Графиком функции
имеет хотя бы один корень, принадлежащий отрезку [−1; 1]. Графиком функции 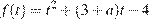 является парабола, ветви которой направлены вверх,
является парабола, ветви которой направлены вверх, 
следовательно, уравнение  имеет хотя бы один корень, принадлежащий отрезку [−1; 1], либо при условии
имеет хотя бы один корень, принадлежащий отрезку [−1; 1], либо при условии 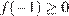 (рис. 1)
(рис. 1) 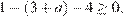 откуда
откуда 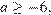 либо при условии
либо при условии 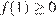 (рис. 2)
(рис. 2)  откуда
откуда 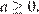
Ответ: 
21. C 6. Каждый из группы учащихся сходил в кино или в театр, при этом возможно, что кто-то из них мог сходить и в кино, и в театр. Известно, что в театре мальчиков было не более  от общего числа учащихся группы, посетивших театр, а в кино мальчиков было не более
от общего числа учащихся группы, посетивших театр, а в кино мальчиков было не более  от общего числа учащихся группы, посетивших кино.
от общего числа учащихся группы, посетивших кино.
а) Могло ли быть в группе 10 мальчиков, если дополнительно известно, что всего в группе было 20 учащихся?
б) Какое наибольшее количество мальчиков МОГЛО быть в группе, если дополнительно известно, что всего в группе было 20 учащихся?
в) Какую наименьшую долю могли составлять девочки от общего числа учащихся в группе без дополнительного условия пунктов а и б?
Решение.
а) Если группа состоит из 3 мальчиков, посетивших только театр, 7 мальчиков, посетивших только кино, и 10 девочек, сходивших и в театр, и в кино, то условие задачи выполнено. Значит, в группе из 20 учащихся могло быть 10 мальчиков.
б) Предположим, что мальчиков было 11 или больше. Тогда девочек было 9 или меньше. Театр посетило не более 3 мальчиков, поскольку если бы их было 3 или больше, то доля мальчиков в театре была бы не меньше 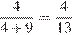 , что больше
, что больше  . Аналогично, кино посетило не более 7 мальчиков, поскольку
. Аналогично, кино посетило не более 7 мальчиков, поскольку  но тогда хотя бы один мальчик не посетил ни театра, ни кино, что противоречит условию.
но тогда хотя бы один мальчик не посетил ни театра, ни кино, что противоречит условию.
В предыдущем пункте было показано, что в группе из 20 учащихся могло быть 10 мальчиков. Значит, наибольшее количество мальчиков в группе — 10.
в) Предположим, что некоторый мальчик сходил и в театр, и в кино. Если бы вместо него в группе присутствовало два мальчика, один из которых посетил только театр, а другой — только кино, то доля мальчиков и в театре, и в кино осталась бы прежней, а общая доля девочек стала бы меньше. Значит, для оценки наименьшей доли девочек в группе можно считать, что каждый мальчик сходил или только в театр, или только в кино.
Пусть в группе 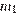 мальчиков, посетивших театр,
мальчиков, посетивших театр,  мальчиков, посетивших кино, и
мальчиков, посетивших кино, и 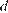 девочек. Оценим долю девочек в этой группе. Нулем считать, что все девочки ходили и в театр, и в кино, поскольку их доля в группе от этого не изменится, а доля в театре и в кино не уменьшится.
девочек. Оценим долю девочек в этой группе. Нулем считать, что все девочки ходили и в театр, и в кино, поскольку их доля в группе от этого не изменится, а доля в театре и в кино не уменьшится.
По условию
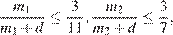
значит,  Тогда
Тогда 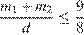 , поэтому доля девочек в группе:
, поэтому доля девочек в группе:

Если группа состоит из 3 мальчиков, посетивших только театр, 6 мальчиков, посетивших только кино, и 8 девочек, сходивших и в театр, и в кино, то условие задачи выполнено, а доля девочек в группе равна 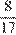 .
.
Ответ: а) да: б) 10; в) 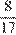 .
.
ОТВЕТЫ Вариант № 15
1. B 1. Для приготовления маринада для огурцов на 1 литр воды требуется 12 г лимонной кислоты. Лимонная кислота продается в пакетиках по 10 г. Какое наименьшее число пачек нужно купить хозяйке для приготовления 6 литров маринада?
Решение.
Для приготовления 6 литров маринада потребуется 12  6 = 72 г лимонной кислоты. Разделим 72 на 10:
6 = 72 г лимонной кислоты. Разделим 72 на 10:
 .
.
Значит, нужно будет купить 8 пакетиков.
Ответ: 8.
2. B 2. 1 киловатт-час электроэнергии стоит 1 рубль 80 копеек. Счетчик электроэнергии 1 ноября показывал 12 625 киловатт-часов, а 1 декабря показывал 12 802 киловатт-часа. Сколько рублей нужно заплатить за электроэнергию за ноябрь?
Решение.
Расход электроэнергии за ноябрь составляет 12 802 − 12 625 = 177 киловатт-часов. Значит, за ноябрь нужно заплатить 1,8  177 = 318,6 рубля.
177 = 318,6 рубля.
Ответ: 318,6.
3. B 3.  Когда самолет находится в горизонтальном полете, подъемная сила, действующая на крылья, зависит только от скорости. На рисунке изображена эта зависимость для некоторого самолета. На оси абсцисс откладывается скорость (в километрах в час), на оси ординат — сила (в тоннах силы). Определите по рисунку, чему равна подъемная сила (в тоннах силы) при скорости 200 км/ч?
Когда самолет находится в горизонтальном полете, подъемная сила, действующая на крылья, зависит только от скорости. На рисунке изображена эта зависимость для некоторого самолета. На оси абсцисс откладывается скорость (в километрах в час), на оси ординат — сила (в тоннах силы). Определите по рисунку, чему равна подъемная сила (в тоннах силы) при скорости 200 км/ч?
Решение.
Из графика видно, что при скорости 200 км в час действующая на крылья подъемная сила равна одной тонне силы.
Ответ: 1.
4. B 4. Интернет-провайдер (компания, оказывающая услуги по подключению к сети Интернет) предлагает три тарифных плана.
| Тарифный план | Абонентская плата | Плата за трафик |
| План «0» | Нет | 2,5 руб. за 1 Мб |
| План «500» | 550 руб. за 500 Мб трафика в месяц | 2 руб. за 1 Мб сверх 500 Мб |
| План «800» | 700 руб. за 800 Мб трафика в месяц | 1,5 руб. за 1 Мб сверх 800 Мб |
Пользователь предполагает, что его трафик составит 600 Мб в месяц и, исходя из этого, выбирает наиболее дешевый тарифный план. Сколько рублей заплатит пользователь за месяц, если его трафик действительно будет равен 600 Мб?
Решение.
Рассмотрим все варианты.
По Плану «0» пользователь потратит 2,5  600 = 1500 руб. в месяц за 600 Мб трафика.
600 = 1500 руб. в месяц за 600 Мб трафика.
По плану «500» он потратит 550 руб. абонентской платы за 500 Мб и 2  100 = 200 руб. сверх того. Поэтому полная плата в месяц составит 550 + 200 = 750 руб.
100 = 200 руб. сверх того. Поэтому полная плата в месяц составит 550 + 200 = 750 руб.
По плану «800» пользователь потратит в месяц за 600 Мб трафика 700 руб.
Наиболее выгодный вариант составляет 700 руб.
Ответ: 700.
5. B 5.  В четырехугольник
В четырехугольник 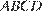 вписана окружность,
вписана окружность,  ,
, 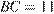 и
и 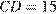 . Найдите четвертую сторону четырехугольника.
. Найдите четвертую сторону четырехугольника.
Решение.
В четырехугольник можно вписать окружность тогда и только тогда, когда  значит,
значит,
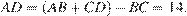
Ответ: 14.
6. B 6. Стрелок стреляет по мишени один раз. В случае промаха стрелок делает второй выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 0,7. Найдите вероятность того, что мишень будет поражена (либо первым, либо вторым выстрелом).
Решение.
Пусть A — событие, состоящее в том, что мишень поражена стрелком с первого выстрела, B — событие, состоящее в том, что мишень поражена со второго выстрела. Вероятность события A равна P (A) = 0,7. Событие B наступает, если, стреляя первый раз, стрелок промахнулся, а, стреляя второй раз, попал. Это независимые события, их вероятность равна произведению вероятностей этих событий: P (B) = 0,3·0,7 = 0,21. События A и B несовместные, вероятность их суммы равна сумме вероятностей этих событий:
P (A + B) = P (A) + P (B) = 0,7 + 0,21 = 0,91.
Ответ: 0,91.
7. B 7. Найдите корень уравнения: 
Решение.
Избавимся от знаменателя:
 .
.
Ответ: 14.
8. B 8. 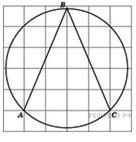 Найдите величину угла
Найдите величину угла 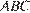 . Ответ дайте в градусах.
. Ответ дайте в градусах.
Решение.
Угол 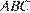 опирается на
опирается на 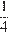 окружности, вписанный угол равен половине дуги, значит,
окружности, вписанный угол равен половине дуги, значит,
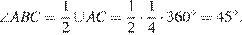
Ответ: 45.
9. B 9. На рисунке изображен график производной функции f(x), определенной на интервале (−7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

Решение.
Промежутки возрастания данной функции f(x) соответствуют промежуткам, на которых ее производная положительна, то есть интервалам (−7; −5,5), (−2,5; 4). Данные интервалы содержат целые точки –6, –2, –1, 0, 1, 2, 3. Их сумма равна –3.
Ответ: –3.
10. B 10. 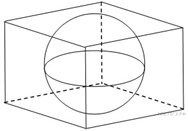 В куб вписан шар радиуса 1. Найдите объем куба.
В куб вписан шар радиуса 1. Найдите объем куба.
Решение.
Ребро куба равно диаметру вписанного в него шара, а объем куба равен кубу его ребра. Отсюда имеем:
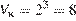 .
.
Ответ: 8.
11. B 11. Найдите значение выражения 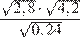 .
.
Решение.
Выполним преобразования:
 .
.
Ответ: 7.
12. B 12. В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону 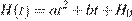 , где
, где 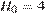 – начальный уровень воды,
– начальный уровень воды, 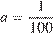 м/мин2, и
м/мин2, и 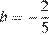 м/мин постоянные,
м/мин постоянные,  – время в минутах, прошедшее с момента открытия крана. В течение какого времени вода будет вытекать из бака? Ответ приведите в минутах.
– время в минутах, прошедшее с момента открытия крана. В течение какого времени вода будет вытекать из бака? Ответ приведите в минутах.
Решение.
Формулой, описывающей уменьшение высоты столба воды с течением времени является
 .
.
Вода будет вытекать из бака, пока её начальный уровень не понизится до нуля. Определим требуемое на это время, решая уравнение 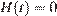 :
:

|
|
|
|
|
Дата добавления: 2015-04-23; Просмотров: 719; Нарушение авторских прав?; Мы поможем в написании вашей работы!