
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные методы экологических исследований 8 страница
|
|
|
|
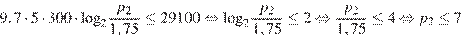 атм.
атм.
Значит, наибольшее давление, до которого можно сжать воздух в колоколе, равно 7 атмосферам.
Ответ: 7.
13. B 13.  Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
Решение.
Из условия  найдем, что радиус такого шара
найдем, что радиус такого шара
 .
.
Ответ: 10.
Первая труба наполняет резервуар на 6 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба?
Решение.
Пусть вторая труба наполняет резервуар за x минут, а первая — за x + 6 минут. В одну минуту они наполняют соответственно  и
и 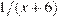 часть резервуара. Поскольку за 4 минуты обе трубы заполняют весь резервуар, за одну минуту они наполняеют одну четвертую часть резервуара:
часть резервуара. Поскольку за 4 минуты обе трубы заполняют весь резервуар, за одну минуту они наполняеют одну четвертую часть резервуара:
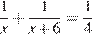 .
.
Далее можно решать полученное уравнение. Но можно заметить, что при положительных x функция, находящаяся в левой части уравнения, убывает. Поэтому очевидное решение уравнения  — единственно. Поскольку вторая труба заполняет
— единственно. Поскольку вторая труба заполняет  резервуара в минуту, она заполнит весь резервуар за 6 минут.
резервуара в минуту, она заполнит весь резервуар за 6 минут.
Ответ: 6.
15. B 15. Найдите точку минимума функции 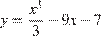 .
.
Решение.
Найдем производную заданной функции:
 .
.
Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка минимума  .
.
Ответ: 3.
16. C 1. а) Решите уравнение 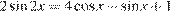 .
.
б) Укажите корни уравнения, принадлежащие отрезку 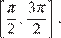 .
.
Решение.
а) Преобразуем уравнение:
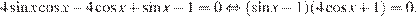
Получаем:  или
или  откуда
откуда
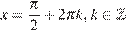 или
или 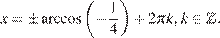
б) С помощью числовой окружности отберем корни на отрезке 
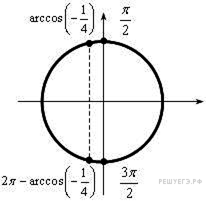

Ответ: а) 
б) 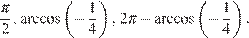
17. C 2. В правильной четырёхугольной пирамиде 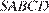 с основанием
с основанием  проведено сечение через середины рёбер
проведено сечение через середины рёбер  и
и 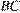 и вершину
и вершину 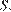 Найдите площадь этого сечения, если боковое ребро пирамиды равно
Найдите площадь этого сечения, если боковое ребро пирамиды равно 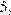 а сторона основания равна
а сторона основания равна 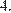
Решение.
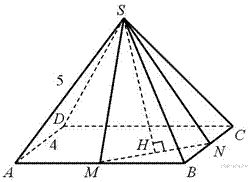 Пусть
Пусть 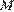 — середина
— середина 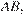 а
а  — середина
— середина  Тогда площадь сечения равна площади треугольника
Тогда площадь сечения равна площади треугольника 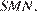 Найдем последовательно
Найдем последовательно 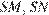 и
и 
 и
и  — медианы треугольников
— медианы треугольников  и
и  соответственно. Так как эти треугольники равнобедренные (поскольку пирамида правильная),
соответственно. Так как эти треугольники равнобедренные (поскольку пирамида правильная),
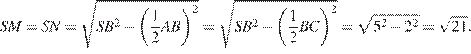
Найдем теперь  из прямоугольного треугольника
из прямоугольного треугольника  В нем катеты равны
В нем катеты равны  Гипотенуза
Гипотенуза  по теореме Пифагора, будет равна
по теореме Пифагора, будет равна 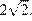
Теперь найдем площадь равнобедренного треугольника  Для этого проведем высоту
Для этого проведем высоту 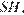 которая, по теореме Пифагора, равна
которая, по теореме Пифагора, равна 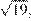 и вычислим площадь:
и вычислим площадь:
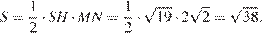
Ответ: 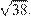
18. C 3. Решите неравенство 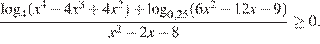
Решение.
Преобразуем неравенство

Сделав замену переменной  получаем:
получаем:
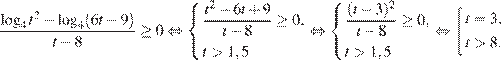
1) 
2) 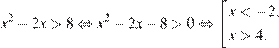
Ответ: 
19. C 4. Угол C треугольника ABC равен 60°, D — отличная от A точка пересечения окружностей, построенных на сторонах AB и AC как на диаметрах. Известно, что ВD: DC = 1: 3. Найдите синус угла A.
Решение.
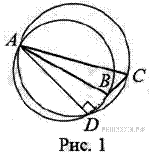
Пусть BD = x, тогда по условию DC = 3 x.
Поскольку D — точка пересечения окружностей, построенных на сторонах AB и AC как на диаметрах, ∠ ADB = ∠ ADC = 90°, значит, точки В, С и D лежат на одной прямой.
В прямоугольном треугольнике ACD угол ∠ C = 60°, откуда 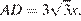 В прямоугольном треугольнике ABD
В прямоугольном треугольнике ABD 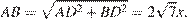
Возможны два случая. Первый случай: угол ABC тупой (рис. 1), тогда точка B лежит между точками D и C, значит, BC = DC − BD = 2 x.
По теореме синусов для треугольника ABC:  откуда
откуда 

Второй случай: угол ABC острый (рис. 2), тогда точка D лежит между точками В и С, значит, BC = DC + BD = 4 х.
По теореме синусов для треугольника ABC: 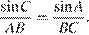 откуда
откуда 
Ответ:  или
или 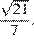
20. C 5. Известно, что значение параметра а таково, что система уравнений
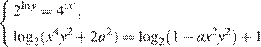
имеет единственное решение. Найдите это значение параметра a и решите систему при найденном значении параметра.
Решение.
Из первого уравнения системы получаем
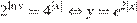 .
.
Заметим, что если пара  — решение системы, то пара
— решение системы, то пара 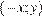 — также решение этой системы. Поскольку система имеет единственное решение, то этим решением может быть только пара
— также решение этой системы. Поскольку система имеет единственное решение, то этим решением может быть только пара 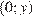 . Таким образом,
. Таким образом,  и из второго уравнения получаем:
и из второго уравнения получаем:
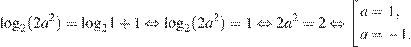
Проверим, действительно ли система при найденных значениях a имеет единственное решение.
1. Если  , то система действительно имеет единственное решение:
, то система действительно имеет единственное решение:
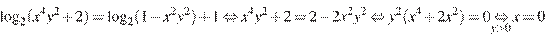 .
.
Тогда
 .
.
2. Если  , то система имеет три решения:
, то система имеет три решения:

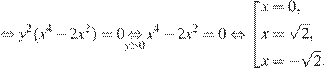
Каждому из найденных значений x соответствует единственное значение
 .
.
Ответ: система имеет единственное решение  при
при  .
.
21. C 6. Задумано несколько целых чисел. Набор этих чисел и их все возможные суммы (по 2, по 3 и т. д.) выписывают на доску в порядке неубывания. Например, если задуманы числа 2, 3, 5, то на доске будет выписан набор 2, 3, 5, 5, 7, 8, 10.
а) На доске выписан набор −6, −2, 1, 4, 5, 7, 11. Какие числа были задуманы?
б) Для некоторых различных задуманных чисел в наборе, выписанном на доске, число 0 встречается ровно 7 раз. Какое наименьшее количество чисел могло быть задумано?
в) Для некоторых задуманных чисел на доске выписан набор. Всегда ли по этому набору можно однозначно определить задуманные числа?
Решение.
а) Если было задумано 4 числа или более, то на доске должно быть записано не менее 15 чисел. Если было задумано 2 числа или меньше, то на доске должно быть записано не более 3 чисел. Значит, было задумано 3 числа. Если бы было задумано 2 отрицательных числа, то на доске было бы выписано не менее трёх отрицательных чисел. Значит, отрицательное число одно, и это число — наименьшее число в наборе, то есть −6. Наибольшее число в наборе 11 является суммой двух положительных задуманных чисел. Из положительных выписанных чисел только 4 и 7 дают в сумме 11. Значит, были задуманы числа −6, 4 и 7.
б) Рассмотрим различные задуманные числа, среди которых нет нуля. Пусть для этих чисел в наборе на доске оказалось ровно k нулей. Если добавить к задуманным числам нуль, то на доске окажется ровно 2 k + 1 нулей: k нулей, получающихся как суммы ненулевых задуманных чисел, k нулей, получающихся как суммы ненулевых задуманных чисел и задуманного нуля, и задуманный нуль. Таким образом, если среди задуманных чисел есть нуль, то в наборе на доске окажется нечётное количество нулей.
Пусть задумано четыре или меньше ненулевых числа. Нуль получается тогда, когда сумма некоторого количества положительных чисел равна по модулю сумме некоторого количества отрицательных чисел. Одно задуманное число даёт одну сумму; два различных задуманных числа одного знака дают три различные суммы; три различных задуманных числа дают семь сумм, среди которых не более двух (задуманное число, наибольшее по модулю, и сумма двух других задуманных чисел) совпадают. Значит, среди сумм положительных и отрицательных чисел совладают по модулю не более трёх. Таким образом, если было задумано не более четырёх различных ненулевых чисел, то на доске окажется не более трёх нулей.
Аналогично, если было задумано не более трёх различных ненулевых чисел, то на доске окажется не более одного нуля. Значит, если было задумано не более четырёх различных чисел, среди которых есть нуль, то на доске окажется не более трёх нулей.
Если были задуманы числа −2; −1; 0; 1; 2, то на доске окажется ровно семь нулей. Значит, наименьшее количество задуманных чисел — 5.
в) Нет, не всегда. Например, для задуманных чисел −3, 1, 2 и −2, −1, 3 на доске будет выписан один и тот же набор −3, −2, −1, 0, 1, 2, 3.
Ответ: а) −6, 4, 7; б) 5; в) нет.
ОТВЕТЫ Вариант № 12
1. B 1. В доме, в котором живет Маша, 9 этажей и несколько подъездов. На каждом этаже находится по 4 квартиры. Маша живет в квартире № 130. В каком подъезде живет Маша?
Решение.
В доме, в котором живет Маша, на девяти этажах каждого подъезда 9  4 = 36 квартир. Разделим 130 на 36:
4 = 36 квартир. Разделим 130 на 36:
 .
.
Значит, Маша живет в 4-м подъезде.
Ответ: 4.
2. B 2. Одна таблетка лекарства весит 20 мг и содержит 5% активного вещества. Ребёнку в возрасте до 6 месяцев врач прописывает 1,4 мг активного вещества на каждый килограмм веса в сутки. Сколько таблеток этого лекарства следует дать ребёнку весом в возрасте четырёх месяцев и весом 5 кг в течение суток?
Решение.
В одной таблетке лекарства содержится 20  0,05 = 1 мг активного вещества. Суточная норма активного вещества для ребенка весом 5 кг составит: 1,4
0,05 = 1 мг активного вещества. Суточная норма активного вещества для ребенка весом 5 кг составит: 1,4  5 = 7 мг. Тем самым, ребенку следует дать 7 таблеток.
5 = 7 мг. Тем самым, ребенку следует дать 7 таблеток.
Ответ: 7.
3. B 3.  На рисунке изображен график осадков в Калининграде с 4 по 10 февраля 1974 г. На оси абсцисс откладываются дни, на оси ординат — осадки в мм.
На рисунке изображен график осадков в Калининграде с 4 по 10 февраля 1974 г. На оси абсцисс откладываются дни, на оси ординат — осадки в мм.
Определите по рисунку, сколько дней из данного периода выпадало от 2 до 8 мм осадков.
Решение.
Из графика видно, что в течение трех дней — 7, 8 и 9 февраля выпадало от 2 до 8 мм осадков.
4. B 4. Независимое агентство каждый месяц определяет рейтинги  новостных сайтов на основе показателей информативности
новостных сайтов на основе показателей информативности  , оперативности
, оперативности  и объективности
и объективности 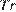 публикаций. Каждый отдельный показатель оценивается целыми числами от −2 до 2. Итоговый рейтинг вычисляется по формуле
публикаций. Каждый отдельный показатель оценивается целыми числами от −2 до 2. Итоговый рейтинг вычисляется по формуле

В таблице даны оценки каждого показателя для нескольких новостных сайтов. Определите наивысший рейтинг новостных сайтов, представленных в таблице. Запишите его в ответ, округлив до целого числа.
| Сайт | Информативность | Оперативность | Объективность |
| VoKak.ru | −1 | ||
| NashiNovosti.com | −2 | −1 | |
| Bezvrak.ru | |||
| Zhizni.net | −1 | −1 | −2 |
Решение.
Рассмотрим все варианты.
Сайт VoKak.ru: 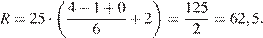
Сайт NashiNovosti.com: 
Сайт Bezvrak.ru: 
Сайт Zhizni.net: 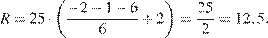
Таким образом, наивысший рейтинг имеет сайт Bezvrak.ru, он равен 75.
Ответ: 75.
5. B 5.  Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (7;9).
Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (7;9).
Решение.
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию. Поэтому
 см2.
см2.
Ответ: 12.
6. B 6. На экзамен вынесено 60 вопросов, Андрей не выучил 3 из них. Найдите вероятность того, что ему попадется выученный билет.
Решение.
Андрей выучил 60 – 3 = 57 вопросов. Поэтому вероятность того, что на экзамене ему попадется выученный билет вопрос равна
 .
.
Ответ: 0,95.
Найдите корень уравнения  .
.
Решение.
Возведем в квадрат:
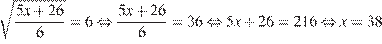 .
.
Ответ: 38.
8. B 8. 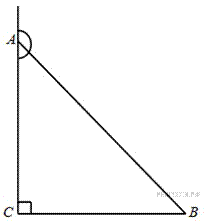
В треугольнике 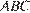 угол
угол  равен 90°, косинус внешнего угла при вершине
равен 90°, косинус внешнего угла при вершине 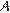 равен –0,6,
равен –0,6, 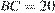 . Найдите
. Найдите 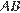 .
.
Решение.
так как
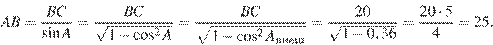
Ответ: 25.
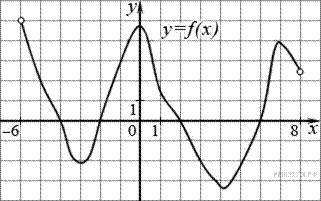
9. B 9. На рисунке изображен график функции 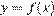 , определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна.
, определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна.
Решение.
Производная функции положительна на тех интервалах, на которых функция возрастает, т. е. на интервалах (−3; 0) и (4,2; 7). В них содержатся целые точки −2, −1, 5 и 6, всего их 4.
Ответ: 4.
10. B 10.  В правильной треугольной пирамиде
В правильной треугольной пирамиде 
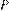 – середина ребра
– середина ребра  ,
, 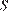 – вершина. Известно, что
– вершина. Известно, что  =5, а
=5, а  =6. Найдите площадь боковой поверхности пирамиды.
=6. Найдите площадь боковой поверхности пирамиды.
Решение.
Отрезок 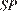 является медианой равнобедренного треугольника
является медианой равнобедренного треугольника 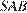 , а значит, и его высотой. Тогда
, а значит, и его высотой. Тогда

Ответ: 45.
11. B 11. Найдите значение выражения  при
при 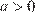 .
.
Решение.
Выполним перобразования:
 .
.
Ответ: 4.
12. B 12. Очень лeгкий заряженный металлический шарик зарядом  Кл скатывается по гладкой наклонной плоскости. В момент, когда его скорость составляет
Кл скатывается по гладкой наклонной плоскости. В момент, когда его скорость составляет 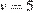 м/с, на него начинает действовать постоянное магнитное поле, вектор индукции
м/с, на него начинает действовать постоянное магнитное поле, вектор индукции 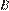 которого лежит в той же плоскости и составляет угол
которого лежит в той же плоскости и составляет угол  с направлением движения шарика. Значение индукции поля
с направлением движения шарика. Значение индукции поля 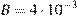 Тл. При этом на шарик действует сила Лоренца, равная
Тл. При этом на шарик действует сила Лоренца, равная 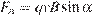 (Н) и направленная вверх перпендикулярно плоскости. При каком наименьшем значении угла
(Н) и направленная вверх перпендикулярно плоскости. При каком наименьшем значении угла  шарик оторвeтся от поверхности, если для этого нужно, чтобы сила
шарик оторвeтся от поверхности, если для этого нужно, чтобы сила 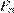 была не менее чем
была не менее чем 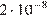 Н? Ответ дайте в градусах.
Н? Ответ дайте в градусах.
Решение.
Задача сводится к решению неравенства 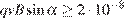 на интервале
на интервале  при заданных значениях заряда шарика
при заданных значениях заряда шарика 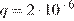 Кл, индукции магнитного поля
Кл, индукции магнитного поля 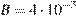 Тл и скорости
Тл и скорости  м/с:
м/с:
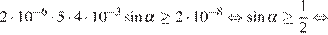
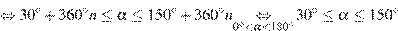 .
.
Ответ: 30.
13. B 13.  Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
Решение.
Площадь основания конуса равна  , а площадь боковой поверхности
, а площадь боковой поверхности  . Из условия имеем:
. Из условия имеем:

Значит, в прямоугольном треугольнике, образованном высотой, образующей и радиусом основания конуса, катет, равный радиусу, вдвое меньше гипотенузы. Тогда он лежит напротив угла  . Следовательно, угол между образующей конуса и плоскостью основания равен
. Следовательно, угол между образующей конуса и плоскостью основания равен  .
.
Ответ: 60.
14. B 14. Васе надо решить 490 задач. Ежедневно он решает на одно и то же количество задач больше по сравнению с предыдущим днем. Известно, что за первый день Вася решил 5 задач. Определите, сколько задач решил Вася в последний день, если со всеми задачами он справился за 14 дней.
Решение.
В первый день Вася решил 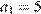 задач, в последний —
задач, в последний — 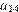 задач. Всего надо решить
задач. Всего надо решить  задач. Поскольку
задач. Поскольку 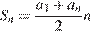 , где
, где  имеем:
имеем:
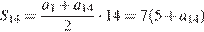 .
.
Тогда
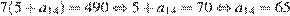 задач.
задач.
|
|
|
|
|
Дата добавления: 2015-04-23; Просмотров: 495; Нарушение авторских прав?; Мы поможем в написании вашей работы!