
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные методы экологических исследований 4 страница
|
|
|
|
Значит, чтобы перевезти всех из лагеря в город, понадобится 6 автобусов.
Ответ: 6.
2. B 2. Оптовая цена учебника 170 рублей. Розничная цена на 20% выше оптовой. Какое наибольшее число таких учебников можно купить по розничной цене на 7000 рублей?
Решение.
С учетом наценки учебник будет стоить 170 + 0,2  170 = 204 рубля. Разделим 7000 на 204:
170 = 204 рубля. Разделим 7000 на 204:
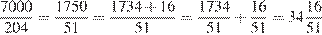 .
.
Значит, можно будет купить 34 учебника.
Ответ: 34.
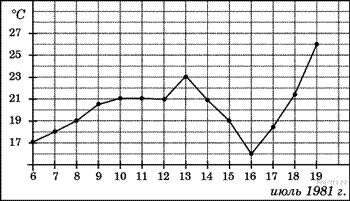 На рисунке жирными точками показана среднесуточная температура воздуха в Бресте каждый день с 6 по 19 июля 1981 года. По горизонтали указываются числа месяца, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку, какая была температура 15 июля. Ответ дайте в градусах Цельсия.
На рисунке жирными точками показана среднесуточная температура воздуха в Бресте каждый день с 6 по 19 июля 1981 года. По горизонтали указываются числа месяца, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку, какая была температура 15 июля. Ответ дайте в градусах Цельсия.
Решение.
Из графика видно, что 15 июля в Бресте было 19 градусов тепла.
Ответ: 19.
4. B 4. В среднем гражданин А. в дневное время расходует 120 кВт  ч электроэнергии в месяц, а в ночное время — 185 кВт
ч электроэнергии в месяц, а в ночное время — 185 кВт  ч электроэнергии. Раньше у А. в квартире был установлен однотарифный счетчик, и всю электроэнергию он оплачивал по тарифу 2,40 руб. за кВт
ч электроэнергии. Раньше у А. в квартире был установлен однотарифный счетчик, и всю электроэнергию он оплачивал по тарифу 2,40 руб. за кВт  ч. Год назад А. установил двухтарифный счётчик, при этом дневной расход электроэнергии оплачивается по тарифу 2,40 руб. за кВт
ч. Год назад А. установил двухтарифный счётчик, при этом дневной расход электроэнергии оплачивается по тарифу 2,40 руб. за кВт  ч, а ночной расход оплачивается по тарифу 0,60 руб. за кВт
ч, а ночной расход оплачивается по тарифу 0,60 руб. за кВт  ч. В течение 12 месяцев режим потребления и тарифы оплаты электроэнергии не менялись. На сколько больше заплатил бы А. за этот период, если бы не поменялся счетчик? Ответ дайте в рублях.
ч. В течение 12 месяцев режим потребления и тарифы оплаты электроэнергии не менялись. На сколько больше заплатил бы А. за этот период, если бы не поменялся счетчик? Ответ дайте в рублях.
Решение.
Рассмотрим оба типа счётчиков.
При использовании однотарифного счётчика, гражданин А. платил в месяц
(120 кВт  ч + 185 кВт
ч + 185 кВт  ч)
ч)  2,4 руб. за 1 кВт
2,4 руб. за 1 кВт  ч = 732 руб.
ч = 732 руб.
При использовании двухтарифного счётчика, гражданин А. платит в месяц
120 кВт  ч
ч  2,4 + 185 кВт
2,4 + 185 кВт  ч
ч  0,6 = 399 руб.
0,6 = 399 руб.
Установка нового типа счётчика позволяет экономить 732 − 399 = 333 руб. в месяц или 333  12 = 3996 руб. в год.
12 = 3996 руб. в год.
5. B 5. 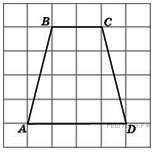 Найдите среднюю линию трапеции
Найдите среднюю линию трапеции 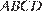 , если стороны квадратных клеток равны 1.
, если стороны квадратных клеток равны 1.
Решение.
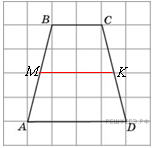
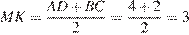 .
.
Ответ: 3.
6. B 6. В фирме такси в данный момент свободно 20 машин: 10 черных, 2 желтых и 8 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси.
Решение.
Вероятность того, что к заказчице приедет зеленое такси равна
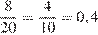 .
.
Ответ: 0,4.
7. B 7. Решите уравнение 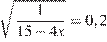 .
.
Решение.
Возведем в квадрат:
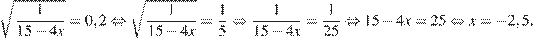
Ответ: −2,5.
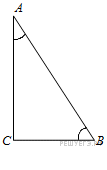
8. B 8. В треугольнике 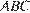 угол
угол  равен 90°,
равен 90°, 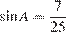 . Найдите
. Найдите 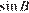 .
. 
Решение.
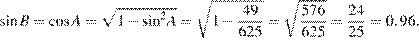
Ответ: 0,96.
9. B 9. Прямая 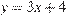 является касательной к графику функции
является касательной к графику функции 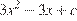 . Найдите
. Найдите  .
.
Решение.
Условие касания графика функции 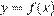 и прямой
и прямой 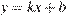 задаётся системой требований:
задаётся системой требований:
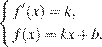
В нашем случае имеем:
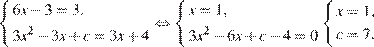
Ответ: 7.
10. B 10. 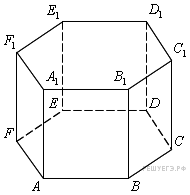 Найдите объем многогранника, вершинами которого являются точки
Найдите объем многогранника, вершинами которого являются точки 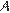 ,
, 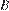 ,
,  ,
,  ,
, 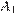 ,
, 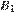 ,
, 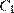 ,
, 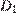 правильной шестиугольной призмы
правильной шестиугольной призмы 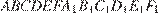 , площадь основания которой равна 6, а боковое ребро равно 2.
, площадь основания которой равна 6, а боковое ребро равно 2.
Решение.
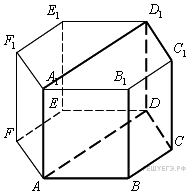 Площадь основания четырехугольной призмы равна половине площади основания правильной шестиугольной призмы, а высота у них общая. Поэтому
Площадь основания четырехугольной призмы равна половине площади основания правильной шестиугольной призмы, а высота у них общая. Поэтому
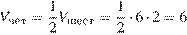 .
.
Ответ: 6.
11. B 11. Найдите значение выражения 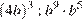 при
при 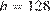 .
.
Решение.
Выполним преобразования:
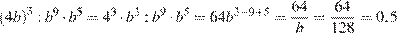 .
.
Ответ: 0,5.
Водолазный колокол, содержащий в начальный момент времени  моля воздуха объeмом
моля воздуха объeмом  л, медленно опускают на дно водоeма. При этом происходит изотермическое сжатие воздуха до конечного объeма
л, медленно опускают на дно водоeма. При этом происходит изотермическое сжатие воздуха до конечного объeма 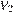 . Работа, совершаемая водой при сжатии воздуха, определяется выражением
. Работа, совершаемая водой при сжатии воздуха, определяется выражением 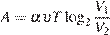 (Дж), где
(Дж), где 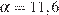 постоянная, а
постоянная, а 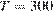 К — температура воздуха. Какой объeм
К — температура воздуха. Какой объeм 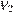 (в литрах) станет занимать воздух, если при сжатии газа была совершена работа в 27 840 Дж?
(в литрах) станет занимать воздух, если при сжатии газа была совершена работа в 27 840 Дж?
Решение.
Задача сводится к решению уравнения 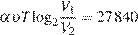 при заданных значениях постоянной
при заданных значениях постоянной 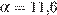 , температуры воздуха
, температуры воздуха  К, количества воздуха
К, количества воздуха  моль и объема воздуха
моль и объема воздуха  л:
л:
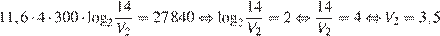 л.
л.
Значит, объем, который будет занимать воздух, равен 3,5 л.
Ответ: 3,5.
13. B 13. 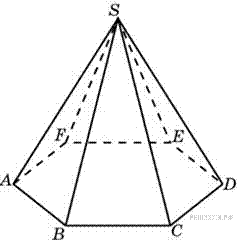 Сторона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды.
Сторона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды.
Решение.
В правильном шестиугольнике сторона равна радиусу описанной окружности, поэтому найдем высоту пирамиды по теореме Пифагора: 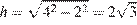 . Площадь основания
. Площадь основания
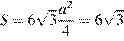 .
.
Тогда объем пирамиды
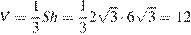 .
.
Ответ: 12.
14. B 14. На изготовление 99 деталей первый рабочий тратит на 2 часа меньше, чем второй рабочий на изготовление 110 таких же деталей. Известно, что первый рабочий за час делает на 1 деталь больше, чем второй. Сколько деталей в час делает второй рабочий?
Решение.
Обозначим  — число деталей, которые изготавливает за час второй рабочий. Тогда первый рабочий за час изготавливает
— число деталей, которые изготавливает за час второй рабочий. Тогда первый рабочий за час изготавливает 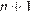 деталь. На изготовление 99 деталей первый рабочий тратит на 2 часа меньше, чем второй рабочий на изготовление 110 таких же деталей, отсюда имеем:
деталь. На изготовление 99 деталей первый рабочий тратит на 2 часа меньше, чем второй рабочий на изготовление 110 таких же деталей, отсюда имеем:
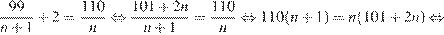
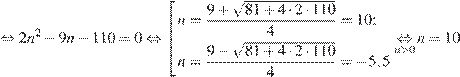 .
.
Таким образом, второй рабочий делает 10 деталей в час.
Ответ: 10.
15. B 15. Найдите точку максимума функции 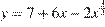 .
.
Решение.
Найдем производную заданной функции:
 .
.
Найдем нули производной:
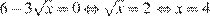 .
.
Определим знаки производной функции и изобразим на рисунке поведение функции:
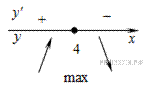
Искомая точка максимума  .
.
Ответ: 4.
16. C 1. а) Решите уравнение 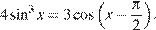
б) Найдите все корни этого уравнения, принадлежащие отрезку 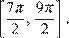
Решение.
 а) Запишем уравнение в виде
а) Запишем уравнение в виде
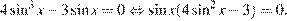
Значит, или 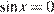 , откуда
, откуда 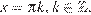 или
или 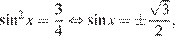 откуда
откуда 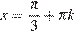 или
или 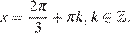
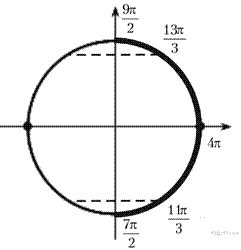
б) С помощью числовой окружности отберем корни, принадлежащие отрезку 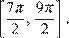 Получим числа:
Получим числа: 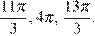
Ответ: а) 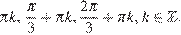 б)
б) 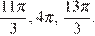
Примечание.
Внимательный читатель, конечно, узнал формулу синуса тройного угла:
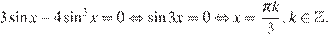
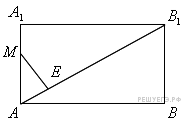
17. C 2. В прямоугольном параллелепипеде 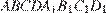 заданы длины ребер
заданы длины ребер 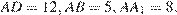 Найдите объем пирамиды
Найдите объем пирамиды 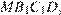 если
если 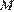 — точка на ребре
— точка на ребре 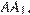 причем
причем 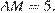
Решение.
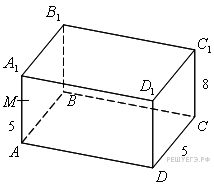
Заметим, что 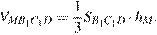 Площадь прямоугольного треугольника, лежащего в основании, равна половине произведения катетов:
Площадь прямоугольного треугольника, лежащего в основании, равна половине произведения катетов: 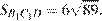
Основание пирамиды лежит в плоскости 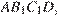 поэтому высотой пирамиды будет являться перпендикуляр, опущенный из точки
поэтому высотой пирамиды будет являться перпендикуляр, опущенный из точки 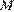 на эту плоскость. Опустим перпендикуляр
на эту плоскость. Опустим перпендикуляр 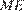 на прямую
на прямую 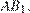 Поскольку
Поскольку 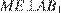 и
и 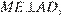 в силу того, что
в силу того, что 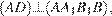 отрезок
отрезок 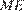 является высотой пирамиды:
является высотой пирамиды: 
Треугольник 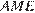 подобен треугольнику
подобен треугольнику 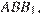 значит,
значит,
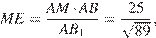
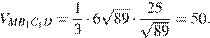
Ответ: 50.
18. C 3. Решите неравенство 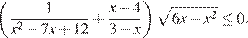
Решение.
Если 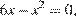 то
то  или
или 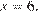 При этих значениях
При этих значениях  выражение
выражение 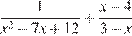 имеет смысл, поэтому
имеет смысл, поэтому  и
и  являются решениями неравенства.
являются решениями неравенства.
Если 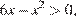 то
то 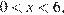 при этом
при этом 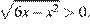 Тогда
Тогда
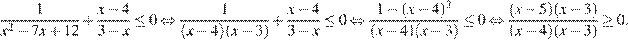
С помощью метода интервалов получаем: 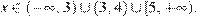 Учитывая условие
Учитывая условие 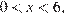 находим:
находим: 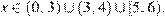
Добавляя точки  и
и 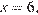 находим все решения заданного неравенства.
находим все решения заданного неравенства.
Ответ: 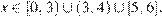
19. C 4. Дана окружность радиуса 4 с центром в точке О, расположенной на биссектрисе угла, равного 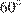 . Найдите радиус окружности, вписанной в данный угол и касающейся данной окружности внешним образом, если известно, что расстояние от точки О до вершины угла равно 10.
. Найдите радиус окружности, вписанной в данный угол и касающейся данной окружности внешним образом, если известно, что расстояние от точки О до вершины угла равно 10.
Решение.
Пусть Q — центр искомой окружности радиуса х, М — точка касания с данной окружностью, В — точка касания с одной из сторон данного угла с вершиной А. Центр окружности, вписанной в угол, лежит на биссектрисе угла, поэтому 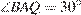 . Из прямоугольного треугольника BAQ находим, что
. Из прямоугольного треугольника BAQ находим, что 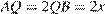 . Пусть точка Q лежит между А и О (рис. 1).
. Пусть точка Q лежит между А и О (рис. 1).
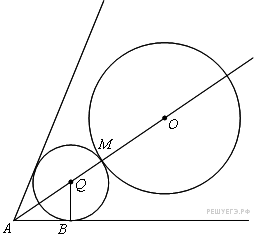
Линия центров касающихся окружностей проходит через точку их касания, поэтому 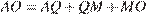 , или
, или 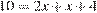 , откуда находим, что
, откуда находим, что  .
.
Пусть точка О лежит между А и Q (рис. 2),
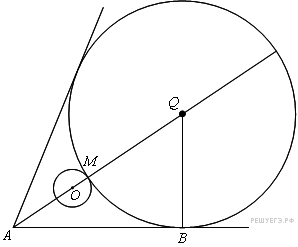
тогда 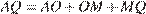 , или
, или 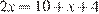 , откуда
, откуда 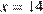 .
.
Ответ: 2 или 14.
20. C 5. Найти все значения 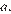 при каждом из которых функция
при каждом из которых функция  имеет более двух точек экстремума.
имеет более двух точек экстремума.
Решение.
1. Функция  имеет вид
имеет вид
а) при 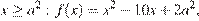 поэтому ее график есть часть параболы с ветвями, направленными вверх, и осью симметрии
поэтому ее график есть часть параболы с ветвями, направленными вверх, и осью симметрии 
б) при 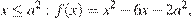 поэтому ее график есть часть параболы с ветвями, направленными вверх, и осью симметрии
поэтому ее график есть часть параболы с ветвями, направленными вверх, и осью симметрии 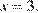
2. Все возможные виды графиков функции показаны на рисунках:
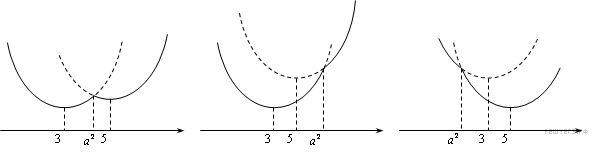
Графики обеих квадратичных функции проходят через точку 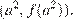
3. Функция 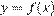 имеет более двух точек экстремума, а именно три, в единственном случае (рис. 1):
имеет более двух точек экстремума, а именно три, в единственном случае (рис. 1):
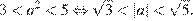
Ответ: 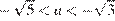 ;
; 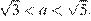
21. C 6. На доске написано число 7. Раз в минуту Вася дописывает на доску одно число: либо вдвое большее какого-то из чисел на доске, либо равное сумме каких-то двух чисел, написанных на доске (таким образом, через одну минуту на доске появится второе число, через две ― третье и т.д.).
а) Может ли в какой-то момент на доске оказаться число 2012?
б) Может ли в какой-то момент сумма всех чисел на доске равняться 63?
в) Через какое наименьшее время на доске может появиться число 784?
Решение.
а) Заметим, что каждое число на доске будет делиться на 7. Действительно, исходное число делится на 7, в случае удвоения числа делящегося на 7, получится число, делящееся на 7. А при сложении чисел, делящихся на 7, также получится число, делящееся на 7. Таким образом, все числа на доске будут делиться на 7, а 2012 на 7 не делится, следовательно, оно не может появиться на доске.
б) Да, может. Пример: 7, 14 (удвоенное число 7), 14 (удвоенное число 7), 14 (удвоенное число 7), 14 (удвоенное число 7). Сумма полученных 5 чисел равна 63.
Замечание. В условии не сказано, что одно число нельзя удваивать несколько раз.
в) Как было замечено в пункте а), все числа на доске будут делиться на 7. Рассмотрим аналогичную задачу, разделив исходное число 7 и то число, которое нужно получить, то есть 784, на 7. От этого количество операций не изменится. Таким образом, достаточно за наименьшее количество операций получить число 112, начав с числа 1.
Заметим, что наибольшее число, которое может получиться на доске через 6 минут, равно 64 (если Вася каждый раз будет удваивать текущее наибольшее число). Следовательно, если в первые 6 минут Вася каждый раз удваивал наибольшее число на доске, то число 112 нельзя получить за 7 минут: если число 64 удвоить, то получится 128, а если прибавить к нему число, не превосходящее 32, то 112 не получится.
В том случае, если в течение первых 6 минут Вася использовал хотя бы одно сложение вместо удвоения, то при первом использовании сложения наибольшее число, записанное на доске увеличилось не более, чем в полтора раза: действительно, в этом случае самый большой результат получится тогда, когда мы к максимальному на данный момент числу прибавим второе по величине, то есть, его половину (напомним, что мы рассматриваем первый случай сложения, то есть до этого были только удвоения). Таким образом, даже если в течение первых 7 минут сделано 6 удвоений и одно сложение (в некотором порядке), то наибольшее число, которое может получиться, равно 96, что меньше 112.
Итак, за 7 минут число 112 получить невозможно.
Приведем пример, как его получить за 8 минут:
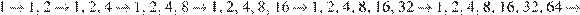
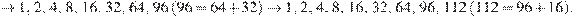
Ответ: а) нет; б) да; в) 8 минут.
ОТВЕТЫ Вариант № 8
На день рождения полагается дарить букет из нечетного числа цветов. Тюльпаны стоят 35 рублей за штуку. У Вани есть 160 рублей. Из какого наибольшего числа тюльпанов он может купить букет Маше на день рождения?
Решение.
Разделим 160 на 35:
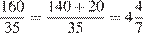 .
.
Ване хватает денег на 4 тюльпана, но цветов должно быть нечетное число. Следовательно, Ваня может купить букет из 3 тюльпанов.
Ответ: 3.
2. B 2. В квартире, где проживает Алексей, установлен прибор учёта расхода холодной воды (счётчик). 1 сентября счётчик показывал расход 103 куб. м воды, а 1 октября — 114 куб. м. Какую сумму должен заплатить Алексей за холодную воду за сентябрь, если цена 1 куб. м холодной воды составляет 19 руб. 20 коп.? Ответ дайте в рублях.
Решение.
Расход воды составил 114 − 103 = 11 куб. м. Поэтому Алексей должен заплатить 11  19,2 = 211,2 руб.
19,2 = 211,2 руб.
Ответ: 211,2.
3. B 3. На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода не выпадало осадков.
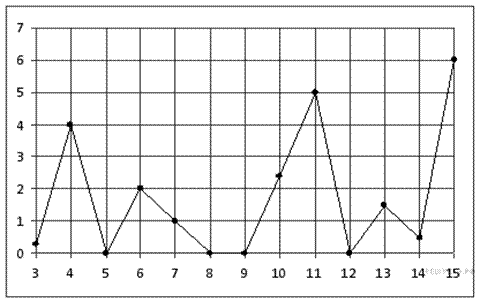
Решение.
Из графика видно, что 4 дня из данного периода (5, 8, 9, 12 февраля) не выпадало осадков (см. рисунок).
Ответ: 4.
4. B 4. Для строительства гаража можно использовать один из двух типов фундамента: бетонный или фундамент из пеноблоков. Для фундамента из пеноблоков необходимо 2 кубометра пеноблоков и 4 мешка цемента. Для бетонного фундамента необходимо 2 тонны щебня и 20 мешков цемента. Кубометр пеноблоков стоит 2450 рублей, щебень стоит 620 рублей за тонну, а мешок цемента стоит 230 рублей. Сколько рублей будет стоить материал, если выбрать наиболее дешевый вариант?
Решение.
Рассмотрим различные варианты.
Стоимость фундамента из пеноблоков складывается из стоимости пеноблоков 2  2 450 = 4 900 руб., а также стоимости цемента 4
2 450 = 4 900 руб., а также стоимости цемента 4  230 = 920 руб. и составляет 920 + 4 900 = 5 820 руб.
230 = 920 руб. и составляет 920 + 4 900 = 5 820 руб.
Стоимость бетонного фундамента складывается из стоимости цемента 20  230 = 4 600 руб., а также стоимости щебня 2
230 = 4 600 руб., а также стоимости щебня 2  620 = 1 240 руб. и составляет 4 600 + 1 240 = 5 840 руб.
620 = 1 240 руб. и составляет 4 600 + 1 240 = 5 840 руб.
|
|
|
|
|
Дата добавления: 2015-04-23; Просмотров: 428; Нарушение авторских прав?; Мы поможем в написании вашей работы!