
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные методы экологических исследований 2 страница
|
|
|
|
На рисунке жирными точками показана среднемесячная температура воздуха в Сочи за каждый месяц 1920 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку наименьшую среднемесячную температуру в период с мая по декабрь 1920 года. Ответ дайте в градусах Цельсия.
Решение.
Из графика видно, что наименьшая среднемесячная температура в период с пятого по двенадцатый месяц (с мая по декабрь) была в ноябре и составляла 6 °C (см. рисунок).
Ответ: 6.
4. B 4. В среднем гражданин А. в дневное время расходует 120 кВт  ч электроэнергии в месяц, а в ночное время — 185 кВт
ч электроэнергии в месяц, а в ночное время — 185 кВт  ч электроэнергии. Раньше у А. в квартире был установлен однотарифный счетчик, и всю электроэнергию он оплачивал по тарифу 2,40 руб. за кВт
ч электроэнергии. Раньше у А. в квартире был установлен однотарифный счетчик, и всю электроэнергию он оплачивал по тарифу 2,40 руб. за кВт  ч. Год назад А. установил двухтарифный счётчик, при этом дневной расход электроэнергии оплачивается по тарифу 2,40 руб. за кВт
ч. Год назад А. установил двухтарифный счётчик, при этом дневной расход электроэнергии оплачивается по тарифу 2,40 руб. за кВт  ч, а ночной расход оплачивается по тарифу 0,60 руб. за кВт
ч, а ночной расход оплачивается по тарифу 0,60 руб. за кВт  ч. В течение 12 месяцев режим потребления и тарифы оплаты электроэнергии не менялись. На сколько больше заплатил бы А. за этот период, если бы не поменялся счетчик? Ответ дайте в рублях.
ч. В течение 12 месяцев режим потребления и тарифы оплаты электроэнергии не менялись. На сколько больше заплатил бы А. за этот период, если бы не поменялся счетчик? Ответ дайте в рублях.
Решение.
Рассмотрим оба типа счётчиков.
При использовании однотарифного счётчика, гражданин А. платил в месяц
(120 кВт  ч + 185 кВт
ч + 185 кВт  ч)
ч)  2,4 руб. за 1 кВт
2,4 руб. за 1 кВт  ч = 732 руб.
ч = 732 руб.
При использовании двухтарифного счётчика, гражданин А. платит в месяц
120 кВт  ч
ч  2,4 + 185 кВт
2,4 + 185 кВт  ч
ч  0,6 = 399 руб.
0,6 = 399 руб.
Установка нового типа счётчика позволяет экономить 732 − 399 = 333 руб. в месяц или 333  12 = 3996 руб. в год.
12 = 3996 руб. в год.
5. B 5. 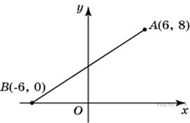 Найдите ординату точки пересечения оси Oy и отрезка, соединяющего точки A (6; 8) и B (−6; 0).
Найдите ординату точки пересечения оси Oy и отрезка, соединяющего точки A (6; 8) и B (−6; 0).
Решение.
Координаты точки, делящей отрезок пополам, считаются по формуле:
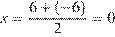 ,
, 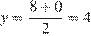 .
.
Видно, что эта точка является искомой.
Ответ: 4.
6. B 6. На семинар приехали 3 ученых из Норвегии, 3 из России и 4 из Испании. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад ученого из России.
Решение.
Всего в семинаре принимает участие 3 + 3 + 4 = 10 ученых, значит, вероятность того, что ученый, который выступает восьмым, окажется из России, равна 3:10 = 0,3.
Ответ: 0,3.
Найдите корень уравнения: 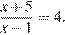
Решение.
Последовательно получаем:
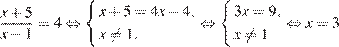 .
.
Ответ: 3.
8. B 8. 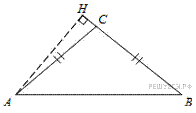 В тупоугольном треугольнике
В тупоугольном треугольнике 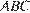
 , высота
, высота 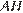 равна 7,
равна 7, 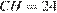 . Найдите
. Найдите 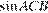 .
.
Решение.
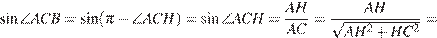
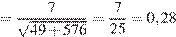 .
.
Ответ: 0,28.
9. B 9. На рисунке изображен график функции y=f(x), определенной на интервале (−2; 12). Найдите сумму точек экстремума функции f(x).

Решение.
Заданная функция имеет максимумы в точках 1, 4, 9, 11 и минимумы в точках 2, 7, 10. Поэтому сумма точек экстремума равна 1 + 4 + 9 + 11 + 2 + 7 + 10 = 44.
Ответ: 44.
10. B 10.  Площадь поверхности куба равна 18. Найдите его диагональ.
Площадь поверхности куба равна 18. Найдите его диагональ.
Решение.
Пусть ребро куба равно  , тогда площадь поверхности куба
, тогда площадь поверхности куба  , а диагональ куба
, а диагональ куба 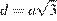 . Тогда
. Тогда
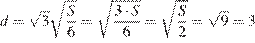 .
.
Ответ: 3.
11. B 11. Найдите значение выражения 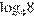 .
.
Решение.
Выполним преобразования:
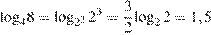 .
.
Ответ: 1,5.
12. B 12. Расстояние от наблюдателя, находящегося на высоте  м над землeй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле
м над землeй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле 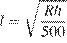 , где
, где 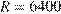 км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 12 км. К пляжу ведeт лестница, каждая ступенька которой имеет высоту 20 см. На какое наименьшее количество ступенек нужно подняться человеку, чтобы он увидел горизонт на расстоянии не менее 44 километров?
км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 12 км. К пляжу ведeт лестница, каждая ступенька которой имеет высоту 20 см. На какое наименьшее количество ступенек нужно подняться человеку, чтобы он увидел горизонт на расстоянии не менее 44 километров?
Решение.
Задача сводится к решению уравнений 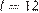 и
и 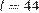 при заданном значении
при заданном значении 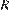 :
:
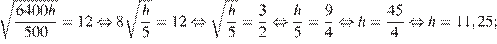
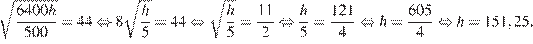
Следовательно, чтобы видеть горизонт на более далеком расстоянии, наблюдателю нужно подняться на 151,25 − 11,25 = 140 метров. Для этого ему необходимо подняться на 140: 0,2 = 700 ступенек.
Ответ: 700.
13. B 13.  Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на
Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на  .
.
Решение.
Площадь осевого сечения цилиндра равна  , так как это прямоугольник. Площадь боковой поверхности
, так как это прямоугольник. Площадь боковой поверхности
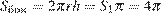 .
.
Ответ: 4.
14. B 14. Два велосипедиста одновременно отправились в 240-километровый пробег. Первый ехал со скоростью, на 1 км/ч большей, чем скорость второго, и прибыл к финишу на 1 час раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч.
Решение.
Пусть  км/ч — скорость велосипедиста, пришедшего к финишу первым, тогда скорость второго велосипедиста —
км/ч — скорость велосипедиста, пришедшего к финишу первым, тогда скорость второго велосипедиста — 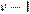 км/ч,
км/ч, 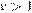 . Первый велосипедист прибыл к финишу на 1 час раньше второго, отсюда имеем:
. Первый велосипедист прибыл к финишу на 1 час раньше второго, отсюда имеем:
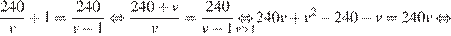
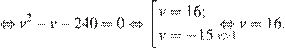
Значит, первым финишировал велосипедист, двигавшийся со скоростью 16 км/ч.
Ответ: 16.
15. B 15. Найдите наименьшее значение функции 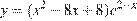 на отрезке
на отрезке 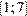 .
.
Решение.
Найдем производную заданной функции:
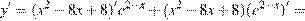
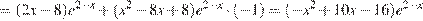 .
.
Найдем нули производной:
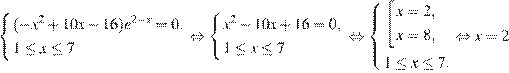 .
.
В точке 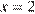 заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:
заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:
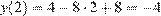 .
.
Ответ: −4.
а) Решите уравнение 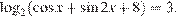
б) Найдите все корни этого уравнения, принадлежащие отрезку 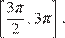
Решение.
 а) Из данного уравнения получаем:
а) Из данного уравнения получаем:

Значит, или 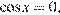 откуда
откуда 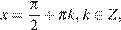 или
или 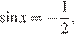 откуда
откуда 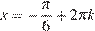 или
или 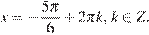
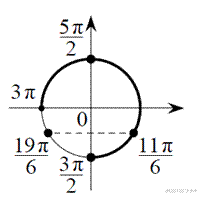
б) С помощью числовой окружности отберём корни, принадлежащие отрезку 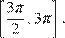 Получим числа:
Получим числа: 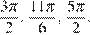
Ответ: а) 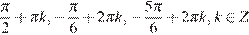 ; б)
; б) 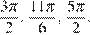
17. C 2. В правильной четырёхугольной призме 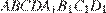 стороны основания равны 2, а боковые рёбра равны 3. На ребре
стороны основания равны 2, а боковые рёбра равны 3. На ребре 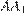 отмечена точка
отмечена точка 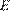 так, что
так, что 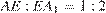 . Найдите угол между плоскостями
. Найдите угол между плоскостями  и
и 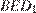 .
.
Решение.
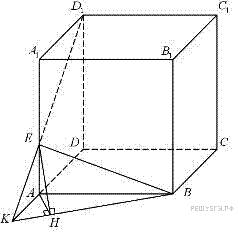 Прямая
Прямая  пересекает прямую
пересекает прямую 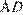 в точке
в точке 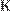 . Плоскости
. Плоскости 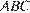 и
и 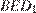 пересекаются по прямой
пересекаются по прямой 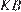 .
.
Из точки  опустим перпендикуляр
опустим перпендикуляр 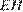 на прямую
на прямую 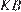 , тогда отрезок
, тогда отрезок 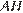 (проекция
(проекция 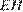 ) перпендикулярен прямой
) перпендикулярен прямой 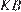 . Угол
. Угол 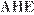 является линейным углом двугранного угла, образованного плоскостями
является линейным углом двугранного угла, образованного плоскостями 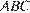 и
и 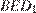 .
.
Поскольку 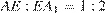 , получаем:
, получаем:
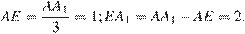
Из подобия треугольников 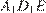 и
и 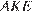 находим:
находим:
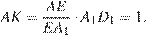
В прямоугольном треугольнике 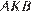 с прямым углом
с прямым углом 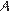 :
: 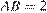 ;
; 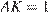 ;
; 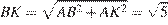 , откуда высота
, откуда высота
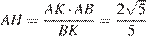 .
.
Из прямоугольного треугольника 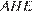 с прямым углом
с прямым углом 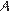 получаем:
получаем:
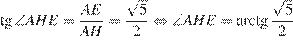 .
.
Ответ может быть представлен и в другой форме: 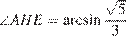 или
или 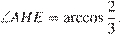
Ответ: 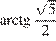 .
.
18. C 3 Решите систему неравенств 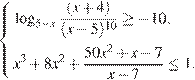
Решение.
1. Решим первое неравенство системы:
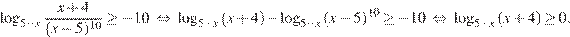
Рассмотрим два случая. Первый случай: 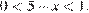 Имеем:
Имеем:
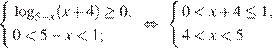
система не имеет решения.
Второй случай: 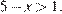 Имеем:
Имеем:
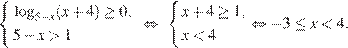
Решение первого неравенства исходной системы: 
2. Решим второе неравенство системы:
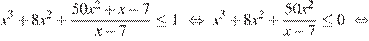
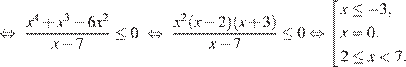
Решение второго неравенства исходной системы: 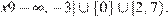
3. Решение исходной системы неравенств: 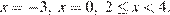
Ответ: 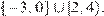
19. C 4. Окружности радиусов 2 и 9 с центрами 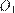 и
и 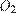 соответственно касаются в точке
соответственно касаются в точке 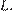 Прямая, проходящая через точку
Прямая, проходящая через точку 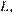 вторично пересекает меньшую окружность в точке
вторично пересекает меньшую окружность в точке 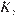 а большую — в точке
а большую — в точке 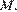 Найдите площадь треугольника
Найдите площадь треугольника 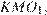 если
если 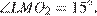
Решение.
Точки 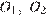 и L лежат на одной прямой. Поскольку треугольники
и L лежат на одной прямой. Поскольку треугольники 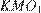 и
и 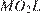 равнобедренные,
равнобедренные, 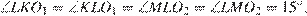 откуда
откуда 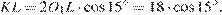
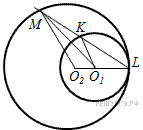
Возможны два случая. Первый случай: окружности касаются внутренним образом (рис. 1), тогда точка 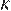 лежит между точками
лежит между точками  и
и 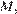 откуда
откуда 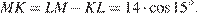

Второй случай: окружности касаются внешним образом (рис. 2), тогда точка 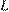 лежит между точками
лежит между точками 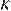 и
и 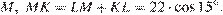
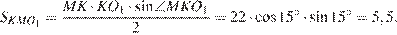
Ответ: 3,5 или 5,5.
20. C 5. Найдите все значения a, при каждом из которых уравнение 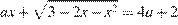 имеет единственный корень.
имеет единственный корень.
Решение.
Запишем уравнение в виде 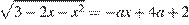 . Рассмотрим две функции:
. Рассмотрим две функции:  и
и 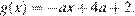 Графиком функции
Графиком функции 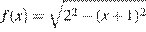 является полуокружность радиуса 2 с центром в точке
является полуокружность радиуса 2 с центром в точке 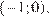 лежащая в верхней полуплоскости (см. рис.). При каждом значении
лежащая в верхней полуплоскости (см. рис.). При каждом значении  графиком функции
графиком функции 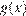 является прямая с угловым коэффициентом
является прямая с угловым коэффициентом 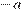 , проходящая через точку
, проходящая через точку 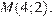
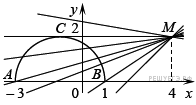
Уравнение имеет единственный корень, если графики функций 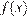 и
и 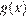 имеют единственную общую точку: либо прямая касается полуокружности, либо пересекает её в единственной точке.
имеют единственную общую точку: либо прямая касается полуокружности, либо пересекает её в единственной точке.
Касательная 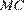 , проведённая из точки
, проведённая из точки 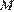 к полуокружности, имеет угловой коэффициент, равный нулю, то есть при
к полуокружности, имеет угловой коэффициент, равный нулю, то есть при  исходное уравнение имеет единственный корень. При
исходное уравнение имеет единственный корень. При  прямая не имеет общих точек с полуокружностью.
прямая не имеет общих точек с полуокружностью.
Прямая 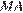 , заданная уравнением
, заданная уравнением 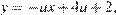 проходит через точки
проходит через точки 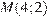 и
и 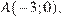 следовательно, её угловой коэффициент
следовательно, её угловой коэффициент 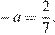
При 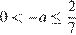 прямая, заданная уравнением
прямая, заданная уравнением 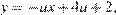 имеет две общие точки с полуокружностью. Прямая
имеет две общие точки с полуокружностью. Прямая  заданная уравнением
заданная уравнением 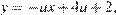 заданная уравнением
заданная уравнением 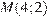 и
и 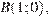 следовательно, её угловой коэффициент
следовательно, её угловой коэффициент 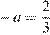 . При
. При 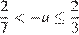 прямая, заданная уравнением
прямая, заданная уравнением 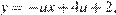 имеет угловой коэффициент больше, чем у прямой
имеет угловой коэффициент больше, чем у прямой 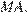 и не больше, чем у прямой
и не больше, чем у прямой 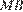 , и пересекает полуокружность в единственной точке. Получаем, что при
, и пересекает полуокружность в единственной точке. Получаем, что при  исходное уравнение имеет единственный корень. При
исходное уравнение имеет единственный корень. При 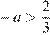 прямая не имеет общих точек с полуокружностью.
прямая не имеет общих точек с полуокружностью.
Ответ: 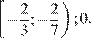
21. C 6. Произведение всех делителей натурального числа 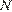 оканчивается на 399 нулей. На сколько нулей может оканчиваться число
оканчивается на 399 нулей. На сколько нулей может оканчиваться число 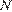 ?
?
Решение.
Разложим 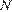 на простые множители:
на простые множители:
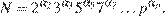
где  — наибольший простой множитель и
— наибольший простой множитель и 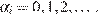 Если запись числа
Если запись числа 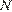 оканчивается
оканчивается  нулями, то или
нулями, то или 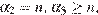 или, наоборот,
или, наоборот, 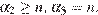
Оценим количество делителей  числа
числа 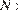
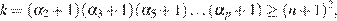
при этом  делится на
делится на 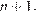
Первый случай. Если  — четное, то все делители разбиваются на
— четное, то все делители разбиваются на 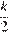 пар вида
пар вида 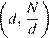 так, что произведение делителей в каждой паре равно
так, что произведение делителей в каждой паре равно 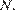 Поэтому произведение всех делителей равно
Поэтому произведение всех делителей равно 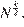
Второй случай. Если  — нечетное, то
— нечетное, то  делителей разбиваются на пары указанного вида, и есть еще один делитель —
делителей разбиваются на пары указанного вида, и есть еще один делитель — 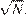 В этом случае тоже произведение всех делителей:
В этом случае тоже произведение всех делителей: 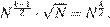
Значит, для любого 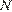 произведение всех делителей оканчивается
произведение всех делителей оканчивается 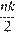 нулями, следовательно,
нулями, следовательно, 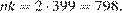 При этом
При этом 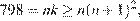 откуда следует, что
откуда следует, что  — делитель числа 798, и
— делитель числа 798, и 
Выпишем все такие 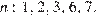 Из равенства
Из равенства 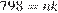 также следует, что 798 делится на
также следует, что 798 делится на 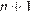 . Поэтому возможно только
. Поэтому возможно только 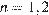 и
и 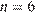 . Для каждого из этих
. Для каждого из этих  подберем
подберем 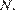 Ограничимся простыми множителями 2 и 5. Значит, нужно подобрать только
Ограничимся простыми множителями 2 и 5. Значит, нужно подобрать только 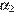 и
и 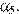
|
|
|
|
|
Дата добавления: 2015-04-23; Просмотров: 447; Нарушение авторских прав?; Мы поможем в написании вашей работы!