Основные методы экологических исследований 5 страница

Пер­вый ва­ри­ант де­шев­ле вто­ро­го.

Ответ: 5820.

5. B 5. На клет­ча­той бу­ма­ге с клет­ка­ми раз­ме­ром 1 см 1 см изоб­ра­жен тре­уголь­ник (см. ри­су­нок). Най­ди­те его пло­щадь в квад­рат­ных сан­ти­мет­рах.

Ре­ше­ние.

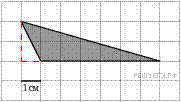Пло­щадь тре­уголь­ни­ка равна по­ло­ви­не про­из­ве­де­ния ос­но­ва­ния на вы­со­ту, про­ве­ден­ную к этому ос­но­ва­нию или его про­дол­же­нию. По­это­му

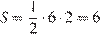см².

Ответ: 6.

6. B 6. При ар­тил­ле­рий­ской стрель­бе ав­то­ма­ти­че­ская си­сте­ма де­ла­ет вы­стрел по цели. Если цель не уни­что­же­на, то си­сте­ма де­ла­ет по­втор­ный вы­стрел. Вы­стре­лы по­вто­ря­ют­ся до тех пор, пока цель не будет уни­что­же­на. Ве­ро­ят­ность уни­что­же­ния не­ко­то­рой цели при пер­вом вы­стре­ле равна 0,4, а при каж­дом по­сле­ду­ю­щем — 0,6. Сколь­ко вы­стре­лов по­тре­бу­ет­ся для того, чтобы ве­ро­ят­ность уни­что­же­ния цели была не менее 0,98?

Ре­ше­ние.

Най­дем ве­ро­ят­ность про­ти­во­по­лож­но­го со­бы­тия, со­сто­я­ще­го в том, что цель не будет уни­что­же­на за n вы­стре­лов. Ве­ро­ят­ность про­мах­нуть­ся при пер­вом вы­стре­ле равна 0,6, а при каж­дом сле­ду­ю­щем — 0,4. Эти со­бы­тия не­за­ви­си­мые, ве­ро­ят­ность их про­из­ве­де­ния равна про­из­ве­де­нию ве­ро­ят­но­сти этих со­бы­тий. По­это­му ве­ро­ят­ность про­мах­нуть­ся при n вы­стре­лах равна: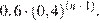

Оста­лось найти наи­мень­шее на­ту­раль­ное ре­ше­ние не­ра­вен­ства

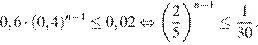
По­сле­до­ва­тель­но про­ве­ряя зна­че­ния , рав­ные 1, 2, 3 и т. д. на­хо­дим, что ис­ко­мым ре­ше­ни­ем яв­ля­ет­ся . Сле­до­ва­тель­но, не­об­хо­ди­мо сде­лать 5 вы­стре­лов.

Ответ: 5.

При­ме­ча­ние.

Можно ре­шать за­да­чу «по дей­стви­ям», вы­чис­ляя ве­ро­ят­ность уце­леть после ряда по­сле­до­ва­тель­ных про­ма­хов:

Р(1) = 0,6.

Р(2) = Р(1)·0,4 = 0,24.

Р(3) = Р(2)·0,4 = 0,096.

Р(4) = Р(3)·0,4 = 0,0384;

Р(5) = Р(4)·0,4 = 0,01536.

По­след­няя ве­ро­ят­ность мень­ше 0,02, по­это­му до­ста­точ­но пяти вы­стре­лов по ми­ше­ни.

При­ве­дем дру­гое ре­ше­ние.

Ве­ро­ят­ность по­ра­зить ми­шень равна сумме ве­ро­ят­но­стей по­ра­зить ее при пер­вом, вто­ром, тре­тьем и т. д. вы­стре­лах. По­это­му за­да­ча сво­дит­ся к на­хож­де­нию наи­мень­ше­го на­ту­раль­но­го ре­ше­ния не­ра­вен­ства

В нашем слу­чае не­ра­вен­ство ре­ша­ет­ся под­бо­ром, в общем слу­чае по­на­до­бит­ся фор­му­ла суммы гео­мет­ри­че­ской про­грес­сии, ис­поль­зо­ва­ние ко­то­рой све­дет за­да­чу к про­стей­ше­му ло­га­риф­ми­че­ско­му не­ра­вен­ству.

Ре­ши­те урав­не­ние .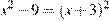

Ре­ше­ние.

По­сле­до­ва­тель­но по­лу­ча­ем:

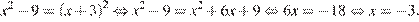
Ответ: −3.

8. B 8. 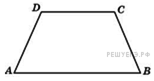Чему равен боль­ший угол рав­но­бед­рен­ной тра­пе­ции, если из­вест­но, что раз­ность про­ти­во­ле­жа­щих углов равна ? Ответ дайте в гра­ду­сах.

Ре­ше­ние.

Раз­ность про­ти­во­ле­жа­щих углов равна , а их сумма равна .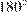

.

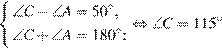Ответ: 115.

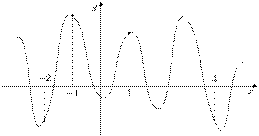
9. B 9. На ри­сун­ке изоб­ра­жен гра­фик функ­ции 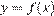и от­ме­че­ны точки −2, −1, 1, 4. В какой из этих точек зна­че­ние про­из­вод­ной наи­мень­шее? В от­ве­те ука­жи­те эту точку.

Ре­ше­ние.

Зна­че­ние про­из­вод­ной в точке ка­са­ния равно уг­ло­во­му ко­эф­фи­ци­ен­ту ка­са­тель­ной, ко­то­рый в свою оче­редь равен тан­ген­су угла на­кло­на дан­ной ка­са­тель­ной к оси абс­цисс. Про­из­вод­ная от­ри­ца­тель­на в точ­ках −1 и 4. Мо­дуль тан­ген­са угла на­кло­на ка­са­тель­ной явно боль­ше в точке 4, по­это­му тан­генс в этой точке наи­мень­ший.

Ответ:4.

10. B 10. 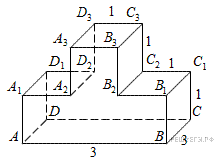Най­ди­те тан­генс угла 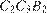мно­го­гран­ни­ка, изоб­ра­жен­но­го на ри­сун­ке. Все дву­гран­ные углы мно­го­гран­ни­ка пря­мые.

Ре­ше­ние.

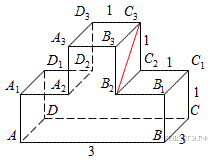Рас­смот­рим пря­мо­уголь­ный тре­уголь­ник 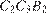. В нем

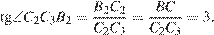
Ответ: 3.

11. B 11. Най­ди­те зна­че­ние вы­ра­же­ния .

Ре­ше­ние.

Ис­поль­зу­ем фор­му­лу си­ну­са двой­но­го угла :

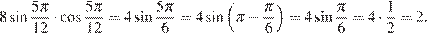
Ответ: 2.

12. B 12. Рас­сто­я­ние от на­блю­да­те­ля, на­хо­дя­ще­го­ся на вы­со­те м над землeй, вы­ра­жен­ное в ки­ло­мет­рах, до ви­ди­мой им линии го­ри­зон­та вы­чис­ля­ет­ся по фор­му­ле , где 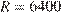км — ра­ди­ус Земли. Че­ло­век, сто­я­щий на пляже, видит го­ри­зонт на рас­сто­я­нии 12 км. К пляжу ведeт лест­ни­ца, каж­дая сту­пень­ка ко­то­рой имеет вы­со­ту 20 см. На какое наи­мень­шее ко­ли­че­ство сту­пе­нек нужно под­нять­ся че­ло­ве­ку, чтобы он уви­дел го­ри­зонт на рас­сто­я­нии не менее 44 ки­ло­мет­ров?

Ре­ше­ние.

За­да­ча сво­дит­ся к ре­ше­нию урав­не­ни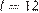й и 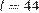при за­дан­ном зна­че­нии :

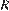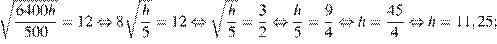
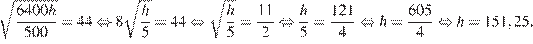
Сле­до­ва­тель­но, чтобы ви­деть го­ри­зонт на более да­ле­ком рас­сто­я­нии, на­блю­да­те­лю нужно под­нять­ся на 151,25 − 11,25 = 140 мет­ров. Для этого ему не­об­хо­ди­мо под­нять­ся на 140: 0,2 = 700 сту­пе­нек.

Ответ: 700.

13. B 13. Объем пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да равен 24. Одно из его ребер равно 3. Най­ди­те пло­щадь грани па­рал­ле­ле­пи­пе­да, пер­пен­ди­ку­ляр­ной этому ребру.

Ре­ше­ние.

Объем пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да равен , где 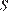– пло­щадь грани, а – вы­со­та пер­пен­ди­ку­ляр­но­го к ней ребра. Тогда пло­щадь грани

.

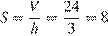Ответ: 8.

14. B 14. Улит­ка пол­зет от од­но­го де­ре­ва до дру­го­го. Каж­дый день она про­пол­за­ет на одно и то же рас­сто­я­ние боль­ше, чем в преды­ду­щий день. Из­вест­но, что за пер­вый и по­след­ний дни улит­ка про­полз­ла в общей слож­но­сти 10 мет­ров. Опре­де­ли­те, сколь­ко дней улит­ка по­тра­ти­ла на весь путь, если рас­сто­я­ние между де­ре­вья­ми равно 150 мет­рам.

Ре­ше­ние.

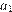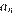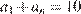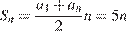Пусть улит­ка про­полз­ла в пер­вый день мет­ров, во вто­рой – , …, в по­след­ний – мет­ров. Тогда м, а за дней про­полз­ла мет­ров. По­сколь­ку всего она про­полз­ла 150 мет­ров, имеем: . Таким об­ра­зом, улит­ка по­тра­ти­ла на весь путь 30 дней.

Ответ: 30.

15. B 15. Най­ди­те наи­мень­шее зна­че­ние функ­ции

Ре­ше­ние.

По­сколь­ку функ­ция 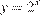воз­рас­та­ю­щая, за­дан­ная функ­ция до­сти­га­ет наи­мень­ше­го зна­че­ния в той же точке, в ко­то­рой до­сти­га­ет наи­мень­ше­го зна­че­ния вы­ра­же­ние 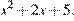Квад­рат­ный трех­член 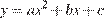с по­ло­жи­тель­ным стар­шим ко­эф­фи­ци­ен­том до­сти­га­ет наи­мень­ше­го зна­че­ния в точке 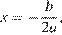в нашем слу­чае — в точке −1. Зна­че­ние функ­ции в этой точке равно

Ответ: 16.

16. C 1. а) Ре­ши­те урав­не­ние

б) Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие про­ме­жут­ку

Ре­ше­ние.

а) За­пи­шем ис­ход­ное урав­не­ние в виде:

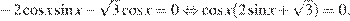
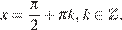Зна­чит, либо от­ку­да либо 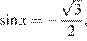от­ку­да или

б) С по­мо­щью чис­ло­вой окруж­но­сти от­бе­рем корни, при­над­ле­жа­щие от­рез­ку По­лу­чим числа:

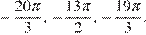
Ответ: а)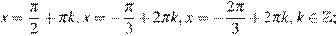

б)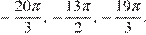

17. C 2. В пра­виль­ную ше­сти­уголь­ную пи­ра­ми­ду, бо­ко­вое ребро ко­то­рой равно 10, а вы­со­та равна 6, впи­са­на сфера. (Сфера ка­са­ет­ся всех гра­ней пи­ра­ми­ды.) Най­ди­те пло­щадь этой сферы.

Ре­ше­ние.

Пусть MH — вы­со­та пра­виль­ной ше­сти­уголь­ной пи­ра­ми­ды MABCDEF с вер­ши­ной M, тогда тре­уголь­ник AMH пря­мо­уголь­ный, MA = 10, MH = 6, от­ку­да

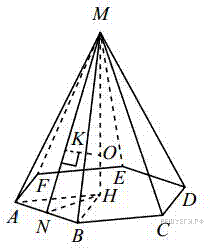
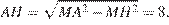
Тре­уголь­ник ABH рав­но­сто­рон­ний, сле­до­ва­тель­но, AB = AH = 8. В тре­уголь­ни­ке AMB вы­со­та

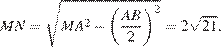
В пра­виль­ном тре­уголь­ни­ке AHB вы­со­та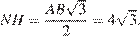

Центр O сферы, впи­сан­ной в пра­виль­ную ше­сти­уголь­ную пи­ра­ми­ду, лежит на её вы­со­те MH, точка K ка­са­ния сферы и бо­ко­вой грани AMB лежит на от­рез­ке MN. Тре­уголь­ни­ки MOK и MNH по­доб­ны, по­это­му

где r — ра­ди­ус сферы. Пло­щадь сферы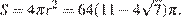

Ответ:

18. C 3. Ре­ши­те си­сте­му не­ра­венств

Ре­ше­ние.

1.Решим пер­вое не­ра­вен­ство

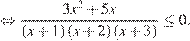
По­лу­ча­ем: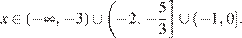

2. Решим вто­рое не­ра­вен­ство:

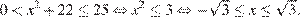
3. Ре­ше­ни­ем си­сте­мы яв­ля­ет­ся общая часть ре­ше­ний двух не­ра­венств. По­сколь­ку 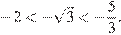по­лу­ча­ем.

Ответ: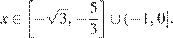

19. C 4. Угол C тре­уголь­ни­ка ABC равен 60°, D — от­лич­ная от A точка пе­ре­се­че­ния окруж­но­стей, по­стро­ен­ных на сто­ро­нах AB и AC как на диа­мет­рах. Из­вест­но, что ВD: DC = 1: 3. Най­ди­те синус угла A.

Ре­ше­ние.

Пусть BD = x, тогда по усло­вию DC = 3 x.

По­сколь­ку D — точка пе­ре­се­че­ния окруж­но­стей, по­стро­ен­ных на сто­ро­нах AB и AC как на диа­мет­рах, ∠ ADB = ∠ ADC = 90°, зна­чит, точки В, С и D лежат на одной пря­мой.

В пря­мо­уголь­ном тре­уголь­ни­ке ACD угол ∠ C = 60°, от­ку­да 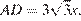В пря­мо­уголь­ном тре­уголь­ни­ке ABD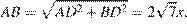

Воз­мож­ны два слу­чая. Пер­вый слу­чай: угол ABC тупой (рис. 1), тогда точка B лежит между точ­ка­ми D и C, зна­чит, BC = DC − BD = 2 x.

По тео­ре­ме си­ну­сов для тре­уголь­ни­ка ABC: от­ку­да

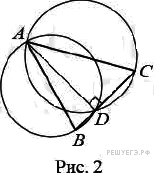
Вто­рой слу­чай: угол ABC ост­рый (рис. 2), тогда точка D лежит между точ­ка­ми В и С, зна­чит, BC = DC + BD = 4 х.

По тео­ре­ме си­ну­сов для тре­уголь­ни­ка ABC: от­ку­да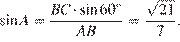

Ответ: 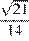или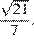

20. C 5. Най­ди­те все зна­че­ния a, при каж­дом из ко­то­рых урав­не­ние

имеет хотя бы один ко­рень.

Ре­ше­ние.

За­пи­шем ис­ход­ное урав­не­ние в виде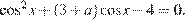

Пусть t = cos x, тогда ис­ход­ное урав­не­ние имеет хотя бы один ко­рень, если урав­не­ние 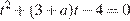имеет хотя бы один ко­рень, при­над­ле­жа­щий от­рез­ку [−1; 1]. Гра­фи­ком функ­ции 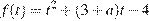яв­ля­ет­ся па­ра­бо­ла, ветви ко­то­рой на­прав­ле­ны вверх,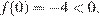

сле­до­ва­тель­но, урав­не­ние 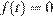имеет хотя бы один ко­рень, при­над­ле­жа­щий от­рез­ку [−1; 1], либо при усло­вии 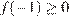(рис. 1) 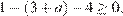от­ку­да 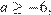либо при усло­вии 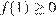(рис. 2) от­ку­да

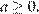
Ответ:

21. C 6. Моток ве­рев­ки режут без остат­ка на куски дли­ной не мень­ше 99 см, но не боль­ше 102 см (на­зо­вем такие куски стан­дарт­ны­ми).

а) Не­ко­то­рый моток ве­рев­ки раз­ре­за­ли на 33 стан­дарт­ных куска, среди ко­то­рых есть куски раз­ной длины. На какое наи­боль­шее число стан­дарт­ных оди­на­ко­вых кус­ков можно было бы раз­ре­зать тот же моток ве­рев­ки?

б) Най­ди­те такое наи­мень­шее число , что любой моток ве­рев­ки, длина ко­то­ро­го боль­ше см, можно раз­ре­зать на стан­дарт­ные куски.

Ре­ше­ние.

Ре­ше­ние каж­до­го пунк­та со­сто­ит из двух ча­стей: оцен­ка и при­мер.

Рас­смот­рим моток ве­рев­ки дли­ной см. Усло­вие того, что его можно раз­ре­зать на стан­дарт­ных кус­ков, за­пи­сы­ва­ет­ся в виде 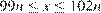или

а) В дан­ном слу­чае имеем 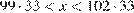(не­ра­вен­ства стро­гие, по­сколь­ку среди кус­ков есть не­рав­ные). Пусть эту ве­рев­ку можно раз­ре­зать на стан­дарт­ных кус­ков, тогда При 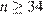по­лу­ча­ем

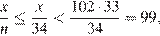
т.е. этот моток ве­рев­ки нель­зя раз­ре­зать боль­ше, чем на 33 стан­дарт­ных куска.

При 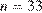по­лу­ча­ем Зна­чит, эту ве­рев­ку можно раз­ре­зать на 33 оди­на­ко­вых стан­дарт­ных куска, но нель­зя раз­ре­зать на боль­шее ко­ли­че­ство стан­дарт­ных кус­ков.

б) От­рез­к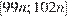и и 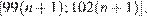яв­ля­ю­щи­е­ся ре­ше­ни­я­ми не­ра­венств 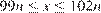и 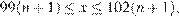имеют общие точки для всех 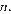при ко­то­рых 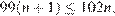то есть при 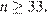Зна­чит, любую ве­рев­ку дли­ной 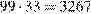см или более можно раз­ре­зать на стан­дарт­ные куски.

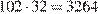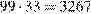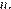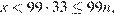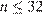До­ка­жем, что ве­рев­ку, длина ко­то­рой боль­ше см, но мень­ше см, нель­зя раз­ре­зать на стан­дарт­ных кус­ков ни для ка­ко­го При по­лу­ча­ем что про­ти­во­ре­чит усло­вию При по­лу­ча­ем 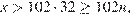что про­ти­во­ре­чит усло­вию 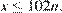Таким об­ра­зом, ис­ко­мое число равно 3267.

Ответ: а) 33; б) 3267.

ОТВЕТЫ Вариант № 9

1. B 1. Каж­дый день во время кон­фе­рен­ции рас­хо­ду­ет­ся 70 па­ке­ти­ков чая. Кон­фе­рен­ция длит­ся 6 дней. Чай про­да­ет­ся в пач­ках по 50 па­ке­ти­ков. Сколь­ко пачек нужно ку­пить на все дни кон­фе­рен­ции?

Ре­ше­ние.

На 6 дней кон­фе­рен­ции рас­хо­ду­ет­ся 70 6 = 420 па­ке­ти­ков чая. Раз­де­лим 420 на 50:

.

Зна­чит, на все дни кон­фе­рен­ции нужно ку­пить 9 пачек чая.

Ответ: 9.

2. B 2. В ма­га­зи­не «Сде­лай сам» вся ме­бель продаётся в разо­бран­ном виде. По­ку­па­тель может за­ка­зать сбор­ку ме­бе­ли на дому, сто­и­мость ко­то­рой со­став­ля­ет 10% от сто­и­мо­сти куп­лен­ной ме­бе­ли. Шкаф стоит 3300 руб­лей. Во сколь­ко руб­лей обойдётся по­куп­ка этого шкафа вме­сте со сбор­кой?

Ре­ше­ние.

Сбор­ка шкафа будет сто­ить 0,1 · 3300 = 330 руб. Цена шкафа вме­сте со сбор­кой со­ста­вит 3300 + 330 = 3630 руб.

Ответ: 3630.

3. B 3 В ходе хи­ми­че­ской ре­ак­ции ко­ли­че­ство ис­ход­но­го ве­ще­ства (ре­а­ген­та), ко­то­рое еще не всту­пи­ло в ре­ак­цию, со вре­ме­нем по­сте­пен­но умень­ша­ет­ся. На ри­сун­ке эта за­ви­си­мость пред­став­ле­на гра­фи­ком. На оси абс­цисс от­кла­ды­ва­ет­ся время в ми­ну­тах, про­шед­шее с мо­мен­та на­ча­ла ре­ак­ции, на оси ор­ди­нат – масса остав­ше­го­ся ре­а­ген­та, ко­то­рый еще не всту­пил в ре­ак­цию (в грам­мах). Опре­де­ли­те по гра­фи­ку, сколь­ко грам­мов ре­а­ген­та всту­пи­ло в ре­ак­цию за три ми­ну­ты?

Ре­ше­ние.

Из гра­фи­ка видно, что в на­чаль­ный мо­мент вре­ме­ни было 20 грам­мов ре­а­ген­та, а через три ми­ну­ты его стало 8 грам­мов. Сле­до­ва­тель­но, про­ре­а­ги­ро­ва­ло 12 грам­мов.

Ответ: 12.

Семья из трех че­ло­век едет из Моск­вы в Че­бок­са­ры. Можно ехать по­ез­дом, а можно — на своей ма­ши­не. Билет на поезд на од­но­го че­ло­ве­ка стоит 930 руб­лей. Ав­то­мо­биль рас­хо­ду­ет 11 лит­ров бен­зи­на на 100 ки­ло­мет­ров пути, рас­сто­я­ние по шоссе равно 700 км, а цена бен­зи­на равна 18,5 руб­лей за литр. Сколь­ко руб­лей при­дет­ся за­пла­тить за наи­бо­лее де­ше­вую по­езд­ку на троих?

Ре­ше­ние.

Сто­и­мость по­езд­ки на по­ез­де для троих че­ло­век будет со­став­лять 930 3 = 2790 руб. Рас­ход бен­зи­на на 700 км пути со­ста­вит 7 раз по 11 лит­ров т. е. 77 лит­ров. Его сто­и­мость 77 18,5 = 1424,5 руб.

Сто­и­мость самой де­ше­вой по­езд­ки со­став­ля­ет 1424,5 рубля.

Ответ: 1424,5.

5. B 5. 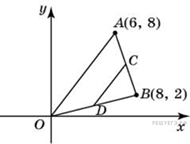Точки O (0; 0), A (6; 8), B (8; 2) яв­ля­ют­ся вер­ши­на­ми тре­уголь­ни­ка. Най­ди­те длину его сред­ней линии CD, па­рал­лель­ной OA.

Ре­ше­ние.

Точки C и D яв­ля­ют­ся се­ре­ди­на­ми сто­рон тре­уголь­ни­ка, тогда

, , , .

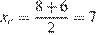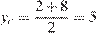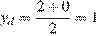По­это­му

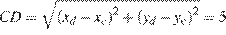
Ответ: 5.

При­ве­дем дру­гое ре­ше­ние.

За­ме­тим, что длина OA равна . Длина сред­ней линии вдвое мень­ше — она равна 5.

6. B 6. В фирме такси в дан­ный мо­мент сво­бод­но 20 машин: 10 чер­ных, 2 жел­тых и 8 зе­ле­ных. По вы­зо­ву вы­еха­ла одна из машин, слу­чай­но ока­зав­ша­я­ся ближе всего к за­каз­чи­це. Най­ди­те ве­ро­ят­ность того, что к ней при­е­дет зе­ле­ное такси.

Ре­ше­ние.

Ве­ро­ят­ность того, что к за­каз­чи­це при­е­дет зе­ле­ное такси равна

.

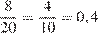Ответ: 0,4.

7. B 7. Най­ди­те ко­рень урав­не­ния:

Ре­ше­ние.

Из­ба­вим­ся от зна­ме­на­те­ля:

.

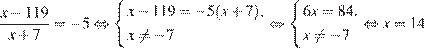Ответ: 14.

8. B 8. 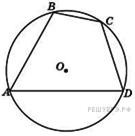Угол 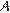че­ты­рех­уголь­ни­ка , впи­сан­но­го в окруж­ность, равен 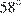. Най­ди­те угол этого че­ты­рех­уголь­ни­ка. Ответ дайте в гра­ду­сах.

Ре­ше­ние.

сумма про­ти­во­по­лож­ных углов че­ты­рех­уголь­ни­ка, впи­сан­но­го в окруж­ность, равна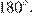

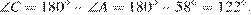
Дата добавления: 2015-04-23