Основные методы экологических исследований 3 страница

1.

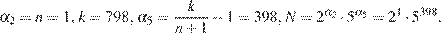
2.

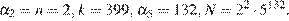
3.

Таким об­ра­зом, для 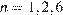най­де­ны (и даже не все) , окан­чи­ва­ю­щи­е­ся ну­ля­ми, про­из­ве­де­ние де­ли­те­лей ко­то­рых окан­чи­ва­ет­ся 399 ну­ля­ми.

Ответ: 1, 2, 6.

ОТВЕТЫ Вариант № 6

На день рож­де­ния по­ла­га­ет­ся да­рить букет из не­чет­но­го числа цве­тов. Тюль­па­ны стоят 35 руб­лей за штуку. У Вани есть 160 руб­лей. Из ка­ко­го наи­боль­ше­го числа тюль­па­нов он может ку­пить букет Маше на день рож­де­ния?

Ре­ше­ние.

Раз­де­лим 160 на 35:

.

Ване хва­та­ет денег на 4 тюль­па­на, но цве­тов долж­но быть не­чет­ное число. Сле­до­ва­тель­но, Ваня может ку­пить букет из 3 тюль­па­нов.

Ответ: 3.

2. B 2. Ма­га­зин за­ку­па­ет цве­точ­ные горш­ки по опто­вой цене 120 руб­лей за штуку и про­да­ет с на­цен­кой 20%. Какое наи­боль­шее число таких горш­ков можно ку­пить в этом ма­га­зи­не на 1000 руб­лей?

Ре­ше­ние.

С уче­том на­цен­ки гор­шок ста­нет сто­ить 120 + 0,2 120 = 144 рубля. Раз­де­лим 1000 на 144:

.

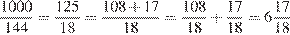Зна­чит, можно будет ку­пить 6 горш­ков.

Ответ: 6.

3. B 3. 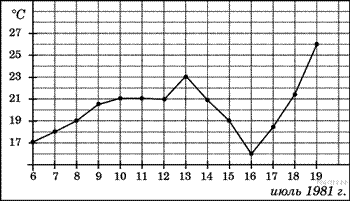На ри­сун­ке жир­ны­ми точ­ка­ми по­ка­за­на сред­не­су­точ­ная тем­пе­ра­ту­ра воз­ду­ха в Бре­сте каж­дый день с 6 по 19 июля 1981 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся числа ме­ся­ца, по вер­ти­ка­ли - тем­пе­ра­ту­ра в гра­ду­сах Цель­сия. Для на­гляд­но­сти жир­ные точки со­еди­не­ны ли­ни­ей. Опре­де­ли­те по ри­сун­ку, сколь­ко дней за ука­зан­ный пе­ри­од тем­пе­ра­ту­ра была ровно 21 °C.

Ре­ше­ние.

Из гра­фи­ка видно, что ровно 21 гра­дус тепла был в Бре­сте 4 дня: 10, 11, 12 и 14 июля.

Ответ: 4.

4. B 4. В пер­вом банке один фунт стер­лин­гов можно ку­пить за 47,4 рубля. Во вто­ром банке 30 фун­тов — за 1446 руб­лей. В тре­тьем банке 12 фун­тов стоят 561 рубль. Какую наи­мень­шую сумму (в руб­лях) при­дет­ся за­пла­тить за 10 фун­тов стер­лин­гов?

Ре­ше­ние.

Рас­смот­рим все ва­ри­ан­ты.

В пер­вом банке 10 фун­тов стер­лин­гов будут сто­ить 47,4 10 = 474 руб.

Во вто­ром банке 10 фун­тов стер­лин­гов стоят 1446: 3 = 482 руб.

В тре­тьем банке 1 фунт стер­лин­гов стоит 561: 12 = 187: 4 = 46,75 руб. Зна­чит, 10 фун­тов стер­лин­гов будут сто­ить 46,75 10 = 467,5 руб.

Ответ: 467,5.

5. B 5. В пря­мо­уголь­ном тре­уголь­ни­ке угол между вы­со­той и бис­сек­три­сой, про­ве­ден­ны­ми из вер­ши­ны пря­мо­го угла, равен 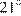. Най­ди­те мень­ший угол дан­но­го тре­уголь­ни­ка. Ответ дайте в гра­ду­сах.

Ре­ше­ние.

мень­шим будет угол 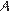, так как угол 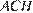в пря­мо­уголь­ном тре­уголь­ни­ке 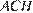оче­вид­но боль­ше, чем угол 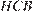в пря­мо­уголь­ном тре­уголь­ни­ке 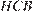. Рас­смот­рим тре­уголь­ник .

.

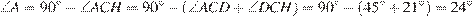Ответ: 24.

6. B 6. В сред­нем из 1000 са­до­вых на­со­сов, по­сту­пив­ших в про­да­жу, 5 под­те­ка­ют. Най­ди­те ве­ро­ят­ность того, что один слу­чай­но вы­бран­ный для кон­тро­ля насос не под­те­ка­ет.

Ре­ше­ние.

в сред­нем из 1000 са­до­вых на­со­сов, по­сту­пив­ших в про­да­жу, 1000 − 5 = 995 не под­те­ка­ют. Зна­чит, ве­ро­ят­ность того, что один слу­чай­но вы­бран­ный для кон­тро­ля насос не под­те­ка­ет, равна

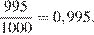
Ответ: 0,995.

7. B 7. Ре­ши­те урав­не­ние 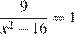. Если урав­не­ние имеет более од­но­го корня, в от­ве­те за­пи­ши­те боль­ший из кор­ней.

Ре­ше­ние.

По­сле­до­ва­тель­но по­лу­ча­ем:

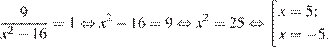
Ответ: 5.

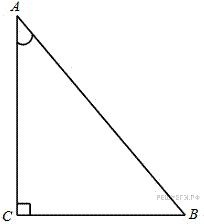
8. B 8. В тре­уголь­ни­ке 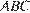угол 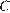равен 90°, 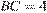, 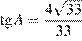. Най­ди­те .

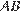Ре­ше­ние.

.

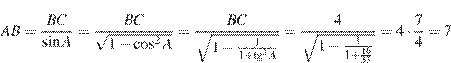Ответ: 7.

9. B 9. На ри­сун­ке изоб­ражён гра­фик функ­ции и во­семь точек на оси абс­цисс: , , 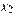, , 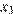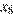. В сколь­ких из этих точек про­из­вод­ная функ­ции по­ло­жи­тель­на?

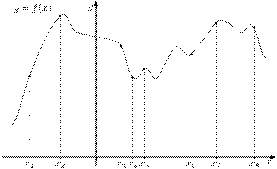
Ре­ше­ние.

По­ло­жи­тель­ным зна­че­ни­ям про­из­вод­ной со­от­вет­ству­ет ин­тер­ва­лы, на ко­то­рых функ­ция 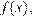воз­рас­та­ет. На них лежат точки 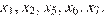Таких точек 5.

Ответ:5.

10. B 10 Пло­щадь по­верх­но­сти куба равна 18. Най­ди­те его диа­го­наль.

Ре­ше­ние.

Пусть ребро куба равно , тогда пло­щадь по­верх­но­сти куба , а диа­го­наль куба 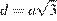. Тогда

.

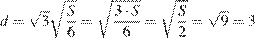Ответ: 3.

11. B 11. Най­ди­те зна­че­ние вы­ра­же­ния .

Ре­ше­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

.

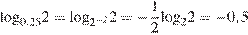Ответ: -0,5.

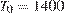12. B 12. За­ви­си­мость тем­пе­ра­ту­ры (в гра­ду­сах Кель­ви­на) от вре­ме­ни для на­гре­ва­тель­но­го эле­мен­та не­ко­то­ро­го при­бо­ра была по­лу­че­на экс­пе­ри­мен­таль­но и на ис­сле­ду­е­мом ин­тер­ва­ле тем­пе­ра­тур опре­де­ля­ет­ся вы­ра­же­ни­ем , где – время в ми­ну­тах, К, 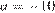К/мин , К/мин. Из­вест­но, что при тем­пе­ра­ту­ре на­гре­ва­те­ля свыше 1760 К при­бор может ис­пор­тить­ся, по­это­му его нужно от­клю­чать. Опре­де­ли­те, через какое наи­боль­шее время после на­ча­ла ра­бо­ты нужно от­клю­чать при­бор. Ответ вы­ра­зи­те в ми­ну­тах.

Ре­ше­ние.

Най­дем, в какой мо­мент вре­ме­ни после на­ча­ла ра­бо­ты тем­пе­ра­ту­ра ста­нет рав­ной 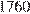К. За­да­ча сво­дит­ся к ре­ше­нию урав­не­ния 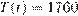при за­дан­ных зна­че­ни­ях па­ра­мет­ров a и b:

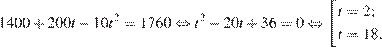
Через 2 ми­ну­ты после вклю­че­ния при­бор на­гре­ет­ся до 1760 К, и при даль­ней­шем на­гре­ва­нии может ис­пор­тить­ся. Таким об­ра­зом, при­бор нужно вы­клю­чить через 2 ми­ну­ты.

Ответ: 2.

13. B 13 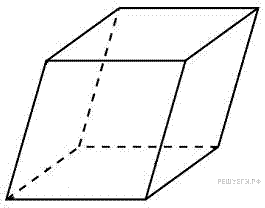Гра­нью па­рал­ле­ле­пи­пе­да яв­ля­ет­ся ромб со сто­ро­ной 1 и ост­рым углом 60 . Одно из ребер па­рал­ле­ле­пи­пе­да со­став­ля­ет с этой гра­нью угол в 60 и равно 2. Най­ди­те объем па­рал­ле­ле­пи­пе­да.

Ре­ше­ние.

Объем па­рал­ле­ле­пи­пе­да 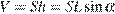, где 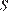– пло­щадь одной из гра­ней, а – длина ребра, со­став­ля­ю­ще­го с этой гра­нью угол . Пло­щадь ромба с ост­рым углом в 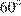равна двум пло­ща­дям рав­но­сто­рон­не­го тре­уголь­ни­ка. Вы­чис­лим объем:

.

Ответ: 1,5.

Пер­вая труба на­пол­ня­ет ре­зер­ву­ар на 6 минут доль­ше, чем вто­рая. Обе трубы на­пол­ня­ют этот же ре­зер­ву­ар за 4 ми­ну­ты. За сколь­ко минут на­пол­ня­ет этот ре­зер­ву­ар одна вто­рая труба?

Ре­ше­ние.

Пусть вто­рая труба на­пол­ня­ет ре­зер­ву­ар за x минут, а пер­вая — за x + 6 минут. В одну ми­ну­ту они на­пол­ня­ют со­от­вет­ствен­но 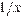и часть ре­зер­ву­а­ра. По­сколь­ку за 4 ми­ну­ты обе трубы за­пол­ня­ют весь ре­зер­ву­ар, за одну ми­ну­ту они на­пол­ня­е­ют одну чет­вер­тую часть ре­зер­ву­а­ра:

.

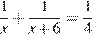Далее можно ре­шать по­лу­чен­ное урав­не­ние. Но можно за­ме­тить, что при по­ло­жи­тель­ных x функ­ция, на­хо­дя­ща­я­ся в левой части урав­не­ния, убы­ва­ет. По­это­му оче­вид­ное ре­ше­ние урав­не­ния 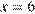— един­ствен­но. По­сколь­ку вто­рая труба за­пол­ня­ет 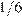ре­зер­ву­а­ра в ми­ну­ту, она за­пол­нит весь ре­зер­ву­ар за 6 минут.

Ответ: 6.

15. B 15. Най­ди­те наи­боль­шее зна­че­ние функ­ции 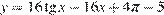на от­рез­ке .

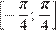Ре­ше­ние.

Най­дем про­из­вод­ную за­дан­ной функ­ции:

Най­ден­ная про­из­вод­ная не­от­ри­ца­тель­на на за­дан­ном от­рез­ке, за­дан­ная функ­ция воз­рас­та­ет на нем, по­это­му наи­боль­шим зна­че­ни­ем функ­ции на от­рез­ке яв­ля­ет­ся

Ответ: 11.

16. C 1 а) Ре­ши­те урав­не­ние

б) Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие про­ме­жут­ку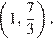

Ре­ше­ние.

а) Пре­об­ра­зу­ем ис­ход­ное урав­не­ние: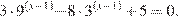

Пусть 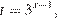тогда урав­не­ние за­пи­шет­ся в виде 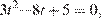от­ку­да или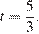

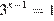При по­лу­чим: от­ку­да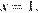

При 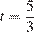по­лу­чим: от­ку­да

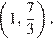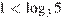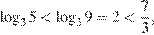б) Ко­рень не при­над­ле­жит про­ме­жут­ку По­сколь­ку и ко­рень 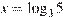при­над­ле­жит про­ме­жут­ку

Ответ: а) 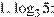б)

17. C 2. В пра­виль­ную ше­сти­уголь­ную пи­ра­ми­ду, бо­ко­вое ребро ко­то­рой равно , а вы­со­та равна 1, впи­са­на сфера. (Сфера ка­са­ет­ся всех гра­ней пи­ра­ми­ды.) Най­ди­те пло­щадь этой сферы.

Ре­ше­ние.

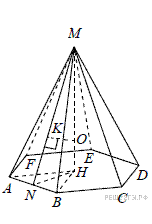Пусть МН — вы­со­та пра­виль­ной ше­сти­уголь­ной пи­ра­ми­ды MABCDEF с вер­ши­ной М, тогда тре­уголь­ник АМН пря­мо­уголь­ный, 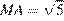, от­ку­да

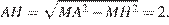
Тре­уголь­ник АВН рав­но­сто­рон­ний, сле­до­ва­тель­но, 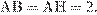В тре­уголь­ни­ке АМВ вы­со­та

В пра­виль­ном тре­уголь­ни­ке АНВ вы­со­та

Центр О сферы, впи­сан­ной в пра­виль­ную ше­сти­уголь­ную пи­ра­ми­ду, лежит на её вы­со­те МН, точка К ка­са­ния сферы и бо­ко­вой грани AMB лежит на от­рез­ке MN. Тре­уголь­ни­ки МОК и MNH по­доб­ны, по­это­му

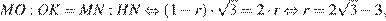
где r — ра­ди­ус сферы.

Пло­щадь сферы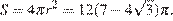

Ответ:

18. C 3. Ре­ши­те си­сте­му не­ра­венств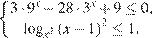

Ре­ше­ние.

1. Решим пер­вое не­ра­вен­ство си­сте­мы. Сде­ла­ем за­ме­ну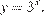

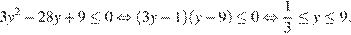
Тогда 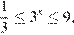от­ку­да на­хо­дим ре­ше­ние пер­во­го не­ра­вен­ства си­сте­мы: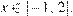

2. Решим вто­рое не­ра­вен­ство си­сте­мы. Рас­смот­рим два слу­чая.

Пер­вый слу­чай: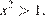

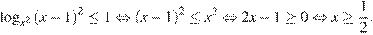
Учи­ты­вая усло­вие 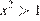, по­лу­ча­ем:

Вто­рой слу­чай: .

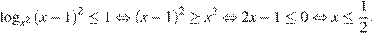
Учи­ты­вая усло­вие , по­лу­ча­ем: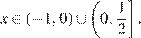

Ре­ше­ние вто­ро­го не­ра­вен­ства си­сте­мы:

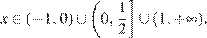
3. Ре­ше­ние си­сте­мы не­ра­венств:

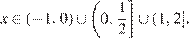
Ответ:

19. C 4. Угол C тре­уголь­ни­ка ABC равен 60°, D — от­лич­ная от A точка пе­ре­се­че­ния окруж­но­стей, по­стро­ен­ных на сто­ро­нах AB и AC как на диа­мет­рах. Из­вест­но, что ВD: DC = 1: 3. Най­ди­те синус угла A.

Ре­ше­ние.

Пусть BD = x, тогда по усло­вию DC = 3 x.

По­сколь­ку D — точка пе­ре­се­че­ния окруж­но­стей, по­стро­ен­ных на сто­ро­нах AB и AC как на диа­мет­рах, ∠ ADB = ∠ ADC = 90°, зна­чит, точки В, С и D лежат на одной пря­мой.

В пря­мо­уголь­ном тре­уголь­ни­ке ACD угол ∠ C = 60°, от­ку­да 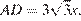В пря­мо­уголь­ном тре­уголь­ни­ке ABD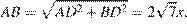

Воз­мож­ны два слу­чая. Пер­вый слу­чай: угол ABC тупой (рис. 1), тогда точка B лежит между точ­ка­ми D и C, зна­чит, BC = DC − BD = 2 x.

По тео­ре­ме си­ну­сов для тре­уголь­ни­ка ABC: от­ку­да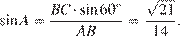

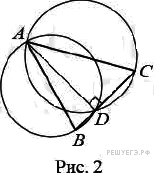
Вто­рой слу­чай: угол ABC ост­рый (рис. 2), тогда точка D лежит между точ­ка­ми В и С, зна­чит, BC = DC + BD = 4 х.

По тео­ре­ме си­ну­сов для тре­уголь­ни­ка ABC: от­ку­да

Ответ: 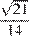или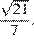

20. C 5. Най­ди­те все зна­че­ния a, при каж­дом из ко­то­рых урав­не­ние

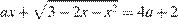
имеет един­ствен­ный ко­рень.

Ре­ше­ние.

За­пи­шем урав­не­ние в виде 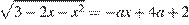Рас­смот­рим две функ­ции: и 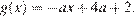Гра­фи­ком функ­ции 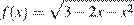яв­ля­ет­ся по­лу­окруж­ность ра­ди­у­са 2 с цен­тром в точке (−1;0), ле­жа­щая в верх­ней по­лу­плос­ко­сти. При каж­дом зна­че­нии гра­фи­ком функ­ции 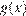яв­ля­ет­ся пря­мая с уг­ло­вым ко­эф­фи­ци­ен­том 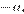про­хо­дя­щая через точку М(4; 2).

Урав­не­ние имеет един­ствен­ный ко­рень, если гра­фи­ки функ­ций и 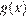имеют един­ствен­ную общую точку: либо пря­мая ка­са­ет­ся по­лу­окруж­но­сти, либо пе­ре­се­ка­ет её в един­ствен­ной точке.

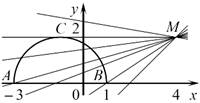
Ка­са­тель­ная МС, про­ведённая из точки M к по­лу­окруж­но­сти, имеет уг­ло­вой ко­эф­фи­ци­ент, рав­ный нулю, то есть при ис­ход­ное урав­не­ние имеет един­ствен­ный ко­рень. При пря­мая не имеет общих точек с по­лу­окруж­но­стью.

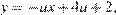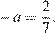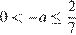Пря­мая МА, за­дан­ная урав­не­ни­ем про­хо­дит через точки М (4; 2) и A (−3;0), сле­до­ва­тель­но, её уг­ло­вой ко­эф­фи­ци­ент При пря­мая, за­дан­ная урав­не­ни­ем 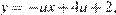имеет уг­ло­вой ко­эф­фи­ци­ент боль­ше, чем у пря­мой МА, и не боль­ше, чем у пря­мой MB, и пе­ре­се­ка­ет по­лу­окруж­ность в един­ствен­ной точке. По­лу­ча­ем, что при ис­ход­ное урав­не­ние имеет един­ствен­ный ко­рень. При пря­мая не имеет общих точек с по­лу­окруж­но­стью.

Ответ:

21. C 6. Длины сто­рон пря­мо­уголь­ни­ка ― на­ту­раль­ные числа, а его пе­ри­метр равен 200. Из­вест­но, что длина одной сто­ро­ны пря­мо­уголь­ни­ка равна n % от длины дру­гой сто­ро­ны, где n – также на­ту­раль­ное число.

а) Какое наи­боль­шее зна­че­ние может при­ни­мать пло­щадь пря­мо­уголь­ни­ка?

б) Какое наи­мень­шее зна­че­ние может при­ни­мать пло­щадь пря­мо­уголь­ни­ка?

в) Най­ди­те все воз­мож­ные зна­че­ния, ко­то­рые может при­ни­мать пло­щадь пря­мо­уголь­ни­ка, если до­пол­ни­тель­но из­вест­но, что n >100.

Ре­ше­ние.

а) Так как пе­ри­метр равен 200, то сумма смеж­ных сто­рон пря­мо­уголь­ни­ка равна 100. Из­вест­но, что наи­боль­шее зна­че­ние пло­ща­ди пря­мо­уголь­ни­ка при фик­си­ро­ван­ном пе­ри­мет­ре до­сти­га­ет­ся в том слу­чае, если он яв­ля­ет­ся квад­ра­том. Таким об­ра­зом, его сто­ро­ны долж­ны быть равны 50, что не про­ти­во­ре­чит усло­вию (длины обеих сто­рон на­ту­раль­ные числа, длина одной сто­ро­ны равна 100% от длины дру­гой). Зна­чит, наи­боль­шее зна­че­ние пло­ща­ди пря­мо­уголь­ни­ка равно 2500.

б) Пусть мень­шая сто­ро­на пря­мо­уголь­ни­ка (или рав­ная дру­гой сто­ро­не, если это квад­рат) равна 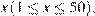тогда дру­гая сто­ро­на равна В этом слу­чае пло­щадь пря­мо­уголь­ни­ка равна 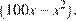Гра­фи­ком дан­ной функ­ции яв­ля­ет­ся па­ра­бо­ла, ветви ко­то­рой на­прав­ле­ны вниз, а число x не пре­вос­хо­дит абс­цис­сы вер­ши­ны па­ра­бо­лы. Сле­до­ва­тель­но, зна­че­ние функ­ции 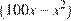будет тем мень­ше, чем даль­ше на­хо­дит­ся число x от абс­цис­сы вер­ши­ны. Таким об­ра­зом, наи­мень­шее зна­че­ние функ­ции до­сти­га­ет­ся при 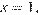а тогда пло­щадь равна 99. В этом слу­чае усло­вие также со­блю­да­ет­ся, так как число 99 равно 9900% от числа 1.

в) Пусть a ― это сто­ро­на, n % от ко­то­рой равны дру­гой сто­ро­не. Тогда дру­гая сто­ро­на равна 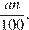По­сколь­ку сумма смеж­ных сто­рон пря­мо­уголь­ни­ка равна 100, по­лу­ча­ем:

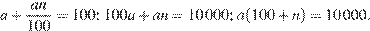
Так как a и n ― целые числа, то число 10 000 крат­но a.

За­ме­тим, что 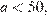так как 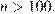Сле­до­ва­тель­но, тре­бу­ет­ся найти все де­ли­те­ли числа, мень­шие 50. Так как 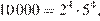то ис­ко­мый де­ли­тель может со­дер­жать в своем раз­ло­же­нии на про­стые мно­жи­те­ли лишь 2 и 5, при­чем каж­дый из этих со­мно­жи­те­лей может быть в сте­пе­ни, не пре­вос­хо­дя­щей 4.

Воз­мож­ны три слу­чая:

1) Число a не де­лит­ся на 5. Тогда оно может быть толь­ко сте­пе­нью двой­ки, при­чем не более, чем чет­вер­той, т.е. a может при­ни­мать зна­че­ния 1, 2, 4, 8 или 16, а пло­щадь при этом будет равна, со­от­вет­ствен­но, 99, 196, 384, 736 или 1344.

2) Число a де­лит­ся на 5, но не де­лит­ся на 25. Тогда оно может быть равно 5, 10, 20 или 40. Пло­щадь в этих слу­ча­ях будет равна, со­от­вет­ствен­но, 475, 900, 1600 или 2400.

3) Число a де­лит­ся на 25. В этом слу­чае оно может быть равно толь­ко 25. Тогда пло­щадь равна 1875.

Ответ: а) 2500; б) 99; в) 99, 196, 384, 475, 736, 900, 1344, 1600, 1875 или 2400.

ОТВЕТЫ Вариант № 7

1. B 1. В лет­нем ла­ге­ре 218 детей и 26 вос­пи­та­те­лей. В ав­то­бус по­ме­ща­ет­ся не более 45 пас­са­жи­ров. Сколь­ко ав­то­бу­сов тре­бу­ет­ся, чтобы пе­ре­вез­ти всех из ла­ге­ря в город?

Ре­ше­ние.

Всего в ла­ге­ре 218 + 26 = 244 чел. Раз­де­лим 244 на 45:

.

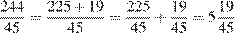Дата добавления: 2015-04-23