
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные методы экологических исследований 14 страница
|
|
|
|
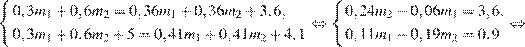
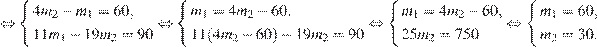
Ответ: 60.
15. B 15. Найдите наименьшее значение функции  на отрезке
на отрезке 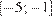 .
.
Решение.
Найдем производную заданной функции:

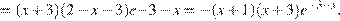
Найдем нули производной:
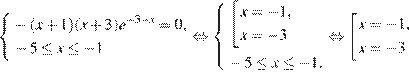
Определим знаки производной функции и изобразим на рисунке поведение функции:
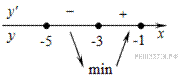
В точке 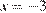 заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:
заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:  .
.
Ответ: 0.
16. C 1. Решите уравнение  .
.
Решение.
Если 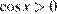 , то решений нет. Если
, то решений нет. Если 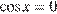 , то
, то 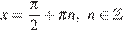 . Если
. Если  , то
, то  , откуда
, откуда 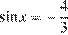 или
или  . Уравнение
. Уравнение 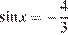 не имеет решений. Учитывая, что
не имеет решений. Учитывая, что  , из уравнения
, из уравнения  получаем:
получаем:
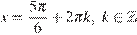 .
.
Ответ:  ;
;  .
.
17. C 2. В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 6, а боковые рёбра равны 12. Найдите площадь сечения пирамиды плоскостью, проходящей через точку C и середину ребра MA параллельно прямой BD.
Решение.
Пусть точка 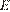 — середина ребра
— середина ребра 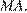 Отрезок
Отрезок 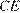 пересекает плоскость
пересекает плоскость 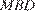 в точке
в точке  В треугольнике
В треугольнике  точка
точка  является точкой пересечения медиан, следовательно,
является точкой пересечения медиан, следовательно,  где
где 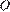 — центр основания пирамиды. Отрезок
— центр основания пирамиды. Отрезок  параллелен
параллелен  и проходит через точку
и проходит через точку  (точка
(точка 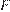 принадлежит ребру
принадлежит ребру  —ребру
—ребру 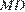 ), откуда
), откуда

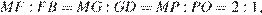
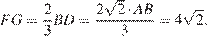
Четырёхугольник  — искомое сечение. Отрезок
— искомое сечение. Отрезок 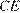 — медиана треугольника
— медиана треугольника 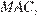 значит,
значит,
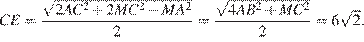
Поскольку прямая 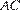 перпендикулярна плоскости
перпендикулярна плоскости  диагонали
диагонали 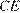 и
и  четырёхугольника
четырёхугольника  перпендикулярны, следовательно,
перпендикулярны, следовательно,

Ответ: 24.
18. C 3. Решите неравенство 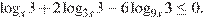
Решение.
Запишем неравенство в виде:

Сделаем замену 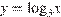 и приведем левую часть к общему знаменателю:
и приведем левую часть к общему знаменателю:

Решением полученного неравенства является множество  Возвращаясь к переменной х, находим множество решений исходного неравенства:
Возвращаясь к переменной х, находим множество решений исходного неравенства: 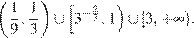
Ответ: 
19. C 4. Расстояние между параллельными прямыми равно  . На одной из них лежит вершина
. На одной из них лежит вершина  , на другой — основание
, на другой — основание 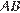 равнобедренного треугольника
равнобедренного треугольника 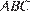 . Известно, что
. Известно, что 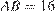 . Найдите расстояние между центрами окружностей, одна из которых вписана в треугольник
. Найдите расстояние между центрами окружностей, одна из которых вписана в треугольник 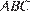 , а вторая касается данных параллельных прямых и боковой стороны треугольника
, а вторая касается данных параллельных прямых и боковой стороны треугольника 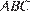 .
.
Решение.
Пусть  — высота треугольника
— высота треугольника 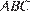 ,
,  и
и  — радиус и центр вписанной окружности,
— радиус и центр вписанной окружности, 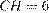 ,
, 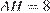 , поэтому
, поэтому 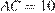 . Найдем площадь, полу периметр и радиус вписанной окружности треугольника
. Найдем площадь, полу периметр и радиус вписанной окружности треугольника 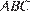 :
:


Тогда 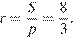 Кроме того, по теореме Пифагора
Кроме того, по теореме Пифагора
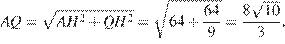
Пусть окружность с центром в точке 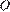 касается боковой стороны
касается боковой стороны 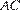 равнобедренного треугольника
равнобедренного треугольника  и данных параллельных прямых. Радиус этой окружности равен
и данных параллельных прямых. Радиус этой окружности равен  , поскольку он вдвое меньше расстояния между прямыми. Точку касания окружности с прямой
, поскольку он вдвое меньше расстояния между прямыми. Точку касания окружности с прямой 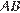 обозначим
обозначим 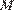 .
.

Пусть точки  и
и  лежат по разные стороны от точки
лежат по разные стороны от точки 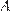 (рис. 1). Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому
(рис. 1). Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому  и
и 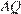 — биссектрисы смежных углов
— биссектрисы смежных углов 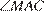 и
и 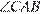 соответственно. Значит,
соответственно. Значит,  и
и  поскольку эти углы образованы парами соответственно перпендикулярных прямых. Следовательно, прямоугольные треугольники
поскольку эти углы образованы парами соответственно перпендикулярных прямых. Следовательно, прямоугольные треугольники  и
и  подобны с коэффициентом
подобны с коэффициентом  Поэтому
Поэтому
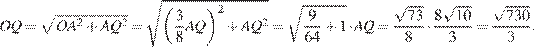

Пусть точки  и
и  лежат по одну сторону от точки
лежат по одну сторону от точки 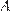 (рис. 2). Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому лучи
(рис. 2). Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому лучи  и
и 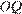 совпадают и являются биссектрисой угла
совпадают и являются биссектрисой угла  Значит, прямоугольные треугольники
Значит, прямоугольные треугольники  и
и 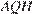 подобны с коэффициентом
подобны с коэффициентом  Тогда
Тогда

Ответ: 
20. C 5. Найдите все значения  , при каждом из которых неравенство
, при каждом из которых неравенство
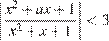
выполняется при всех 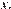
Решение.
Поскольку  для всех значений
для всех значений 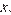 получаем:
получаем:

Решим полученное неравенство:
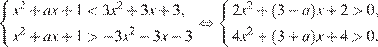
Для того, чтобы любое значение  удовлетворяло этой системе неравенств, нужно, чтобы каждое из неравенств системы было верным для любого значения
удовлетворяло этой системе неравенств, нужно, чтобы каждое из неравенств системы было верным для любого значения  , то есть дискриминанты левых частей этих неравенств должны быть отрицательными:
, то есть дискриминанты левых частей этих неравенств должны быть отрицательными:
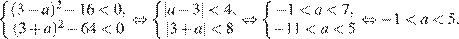
Ответ: 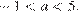
21. C 6. Дано трёхзначное натуральное число (число не может начинаться с нуля), не кратное 100.
а) Может ли частное этого числа и суммы его цифр быть равным 82?
б) Может ли частное этого числа и суммы его цифр быть равным 83?
в) Какое наибольшее натуральное значение может иметь частное данного числа и суммы его цифр?
Решение.
Пусть данное число равно  где
где 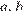 и
и  — цифры сотен, десятков и единиц соответственно. Если частное этого числа и суммы его цифр равно
— цифры сотен, десятков и единиц соответственно. Если частное этого числа и суммы его цифр равно 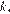 то выполнено
то выполнено 
а) Если  то
то 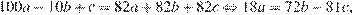 что верно, например, при
что верно, например, при 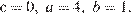 Частное числа 410 и суммы его цифр равно
Частное числа 410 и суммы его цифр равно 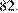
б) Если 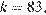 то
то 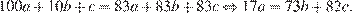 Если
Если  то
то 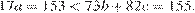 Значит,
Значит, 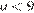 и
и  или
или 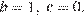 Но ни
Но ни 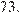 ни
ни 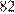 не делится на
не делится на 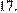 Значит, частное трехзначного числа и суммы его цифр не может быть равным
Значит, частное трехзначного числа и суммы его цифр не может быть равным 
в) Пусть k — наибольшее натуральное значение частного числа, не кратного  и суммы его цифр. Тогда
и суммы его цифр. Тогда 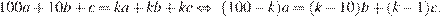 Учитывая, что
Учитывая, что 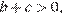 получаем:
получаем:
 то есть
то есть 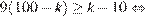
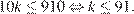
Частное числа  и суммы его цифр равно
и суммы его цифр равно  Значит, наибольшее натуральное значение частного трёхзначного числа, не кратного
Значит, наибольшее натуральное значение частного трёхзначного числа, не кратного  и суммы его цифр равно
и суммы его цифр равно 
Ответ: а) да; б) нет; в) 91.
В настоящее время экология разделилась на ряд научных отраслей и дисциплин, подчас далеких от первоначального понимания экологии как биологической науки об отношениях живых организмов с окружающей средой. Однако в основе всех современных направлений экологии лежат фундаментальные идеи биоэкологии, которая сегодня представляет собой совокупность различных научных направлений. Так, например, выделяют аутэкологию, исследующую индивидуальные связи отдельного организма со средой; популяционную экологию, занимающуюся отношениями между организмами, которые относятся к одному виду и живут на одной территории; синэкологию, комплексно изучающую группы, сообщества организмов и их взаимосвязи в природных системах (экосистемах).
Современная экология представляет собой комплекс научных дисциплин. Базовой является общая экология, изучающая основные закономерности взаимоотношений организмов и условий среды. Теоретическая экология исследует общие закономерности организации жизни, в том числе в связи с антропогенным воздействием на природные системы.
Прикладная экология изучает механизмы разрушения биосферы человеком и способы предотвращения этого процесса, а также разрабатывает принципы рационального использования природных ресурсов. Прикладная экология базируется на системе законов правил и принципов теоретической экологии. Из прикладной экологии выделяются следующие научные направления.
Экология биосферы, изучающая глобальные изменения, происходящие на нашей планете в результате воздействия хозяйственной деятельности человека на природные явления.
Промышленная экология, изучающая влияние выбросов предприятий на окружающую среду и возможности уменьшения этого влияния путем совершенствования технологий и очистных сооружений.
Сельскохозяйственная экология, изучающая способы получения сельскохозяйственной продукции без истощения ресурсов почвы при сохранении окружающей среды.
Медицинская экология, изучающая болезни человека, связанные с загрязнением окружающей среды.
Геоэкология, изучающая строение и механизмы функционирования биосферы, связь и взаимосвязь биосферных и геологических процессов, роль живого вещества в энергетике и эволюции биосферы, участие геологических факторов в возникновении и эволюции жизни на Земле.
Математическая экология моделирует экологические процессы, т.е. изменения в природе, которые могут произойти при изменении экологических условий.
Экономическая экология разрабатывает экономические механизмы рационального природопользования и охраны окружающей среды.
Юридическая экология разрабатывает систему законов, направленных на защиту природы.
Инженерная экология - сравнительно новое направление экологической науки, изучает взаимодействия техники и природы, закономерности формирования региональных и локальных природно- технических систем и способы управления ими в целях защиты природной среды и обеспечения экологической безопасности. Она обеспечивает соответствие техники и технологии промышленных объектов экологическим требованиям
Социальная экология возникла совсем недавно. Лишь в 1986 г. во Львове состоялась первая конференция, посвященная проблемам этой науки. Наука о «доме», или месте обитании социума (человека, общества), изучает планету Земля, а также космос — как жизненную среду социума.
Экология человека - часть социальной экологии, рассматривающая взаимодействие человека как биосоциального существа с окружающим миром.
Валеология - одно из новых самостоятельных ответвлений экологии человека - наука о качестве жизни и здоровье.
Синтетическая эволюционная экология — новая научная дисциплина, включающая частные направления экологии — общую, био-, гео- и социальную.
В экологии часто используются методы, применяемые в других науках, как в биологических (биогеохимия, анатомия, физиология, и др.), так и небиологических (физика, химия, геодезия, метеорология и др.). Но для выявления специфики экологических закономерностей существуют исключительно собственные – экологические методы. Они делятся на полевые, лабораторные, экспериментальные, количественные (математическое моделирование) методы.
Полевые методы имеют первостепенное значение. Они предполагают изучение популяций и сообществ в естественной среде (в природе) и позволяют установить воздействие на объект комплекса факторов, изучить общую картину развития и жизнедеятельности изучаемого объекта.
В качестве примера можно привести леса на склонах разных экспозиций, на разных почвах, на разных географических широтах. Или водные экосистемы на разной глубине в одном и том же море, на одной глубине в южных и северных морях. Все они, несмотря на различия, развиваются по одним и тем же законам, под влиянием комплекса факторов, но значения этих факторов разные и зависят от местоположения объекта исследований.
Однако в полевых исследованиях очень сложно выявить роль одного фактора, как биотического (конкуренции, аллелопатии, плодородия почв), так и абиотического (тепло, влаги, света, засоления, кислотности почв), тем более, что все факторы функционально связаны друг с другом.
Известно, что нередко ограничение одного из них сопряжено с изменением другого. Так, холодность почв с многолетней мерзлотой способствует их переувлажнению и, как следствие, анаэробиозису. В результате резко ухудшаются условия усвоения корнями растений элементов питания. В Приморье, как правило, высокая инсоляция южных склонов сопровождается высокой сухостью субстрата и формированием ксерофитных криволесий.
Исследовать роль конкретного фактора можно при постановке эксперимента в полевых или лабораторных условиях.
Экспериментальные методы отличаются от полевых тем, что организмы искусственно ставятся в условия, при которых можно дозировать размер изучаемого фактора, следовательно, можно точнее, чем при обычном наблюдении, оценить его влияние. При этом выводы, полученные в лаборатории, требуют обязательной проверки в полевых условиях.
В качестве примеров экологических экспериментов можно привести исследования функций лесозащитных полос, изучение осветления насаждений, влияния разных доз удобрений, вносимых под сельскохозяйственные культуры и т.д. Широко известен метод изучения конкурентных взаимоотношений деревьев в лесу путем ограничения определенной площади (площади питания).
Большое значение при проведении экологических исследований имеют химические и физиологические методы, т.к. они позволяют выявить роль разных компонентов экосистем, и в первую очередь, самого главного – фитоценоза, в аккумуляции и превращении вещества и энергии. Химические методы позволяют установить особенности накопления химических элементов в растениях и в целом в сообществах, особенности круговорота питания. С помощью физиологических методов можно в полевых условиях проследить физиологические процессы (фотосинтез и транспирация).
Так как все биосистемы обладают способностью к саморегуляции, т.е. к восстановлению экологического равновесия, а законы их развития имеют причинно-следственную связь, то в экологических исследованиях широкое распространение получили математические методы (математическая статистика, методы теории информации и кибернетики, теории чисел, дифференциальные и интегральные исчисления и др.) и на основе этих методов – моделирование. Моделирование биологических явлений, т.е. воспроизведение в искусственных системах процессов свойственных живой природе, получило широкое распространение в современной экологии.
Модели подразделяются на реальные (аналоговые) и знаковые.
Примеры аналоговых моделей – аппараты искусственного кровообращения, искусственная почка, протезы рук, управляемые биотоками. Аквариумы и океанариумы модели разных водоемов, теплицы – модели экосистем соответствующих природных зон.
Знаковые модели представляют собой отображение оригинала с помощью математических выражений или подробного описания и, в свою очередь, делятся на концептуальные и математические. Первые могут быть представлены текстом, схемами, научными таблицами, графиками и т.д., а вторые – формулами, уравнениями. Математические модели, особенно при наличии количественных характеристик, являются более эффективным методом изучения экосистем. Математические символы позволяют сжато описать сложные экосистемы, а уравнения дают возможность формально выразить взаимодействия различных компонентов экосистем.
Пример простейшего дифференциального уравнения, описывающего рост популяции какого-либо вида на какой-нибудь стадии ее развития (Радкевич, 1997):
dx/dt=rx,
где x – плотность популяции в момент времени t, r – скорость роста в период времени, соответствующий rt. Решением этого уравнения является функция
x=x0ert
Процесс перевода физических или биологических представлений о любой экосистеме в математические формулы и операции над ними называются системным анализом. В современной экологии реальные и знаковые модели используются параллельно, дополняя друг друга. При отсутствии реальных моделей математический подход получается отвлеченным, а при исключении математического подхода бывает трудно уловить смысл реальной модели.
Экологический мониторинг – один из главных методов изучения динамики экосистем (биогеоценозов), происходящей под воздействием естественных и антропогенных факторов. Под мониторингом понимается специальное длительное слежение за состоянием одних и тех же экосистем. Подобные исследования сопряжены с большими время- и трудозатратами, так как предусматривают детальное описание и изучение всех компонентов, составляющих биогеоценоз, и потому возможны лишь при организации стационарных работ с закладкой как временных, так и постоянных пробных площадей. Мониторинг растительного покрова должен проводиться на разных уровнях в соответствии с хорологической (пространственной) дифференциацией биосферных систем. С помощью одной пробной площади размером 1 га проводить мониторинг растительного покрова невозможно. Для равнинного геоботанического района (заповедника) необходимо заложить не менее 10-12 постоянных пробных площадей размером 1 га, а для горного района - не менее 30-40. Именно к такому выводу пришло большинство исследователей, работавших в разных регионах северной Евразии.
К сожалению, изучение процессов, а именно изучение трансформации сложных многокомпонентных систем, какими являются экосистемы и растительные сообщества – это следующий этап развития экологии. Пока что наибольшее развитие получил мониторинг растительного покрова (ботанический), но и он еще находится в начальной стадии.
|
|
|
|
|
Дата добавления: 2015-04-23; Просмотров: 736; Нарушение авторских прав?; Мы поможем в написании вашей работы!