Средняя хронологическая в статистике, способы ее вычисления для интервальных и моментных рядов

Структурные средние величины в статистике.

Структурная средняя. Применяется для характеристики структуры совокупности. К ним относятся показатели моды и медианы. Модой (ϻ) называется варианта признака, которая чаще всего встречается в совокупности.

Размер	Количество пар обуви
38 ϻ

Если имеется интервальный ряд распределения, то мода рассчитывается по формуле:

ϻо=xmo+imo*(fmo-fmo-1)/(fmo-fmo-1)+ (fmo-fmo+1)

xmo – нижняя граница модального интервала

fmo – частота модального интервала

imo – величина модального интервала

fmo-1 – частота интервала, предшествующая модальному

fmo+1 – частота интервала, следующая за модальным.

Модальным называется интервал, имеющий наибольшую частоту. Например: определим модальный процент жирности масла.

Процент жирности	Количество проб
60-65 65-70 70-75 75-80 80-85 85-90	24 ϻ
Итого

80+5(24-20)/(24-20)+(24-10) = 81,1%

Медиана – величина, которая делит численность упорядоченного ряда на 2 равные части. При этом одна часть имеет значение признака меньше медианного, а другая больше медианного. В дискретных рядах с нечетным ранжированием, медиана находится в середине ряда распределения.

В дискретных рядах с четным ранжированием медиана находится как средняя арифметическая простая двух смежных значений признака, стоящих в середине вариационного ряда.

В интервальных рядах медиана определяется по формуле:

ϻe=xme+ime+((1/2*Σfi-S’me-1)/fme)

xme – нижняя граница медианного интервала

fi - сумма частот ряда

S’me-1 - сумма накопленных частот до медианного интервала

fme - частота медианного интервала

= 75+5*(45,5 – 37)/20=77,125

Средняя хронологическая в интервальных рядах определяется путем деления суммы уровней ряда динамики на количество уровней, т.е. по средней арифметической простой.

Для моментных рядов с равностоящими уровнями применяется формула средней хронологической.

ӱ =(½ y1+y2+y3…yn)/(n-1)

Для моментных рядов с не равностоящими уровнями средний уровень ряда рассчитывается по формуле:

ӱ=((у1+у2)f1+(y2+y3)f2+…+(y_n-1+y_n)*f_n)/Σfn

Например: определим среднюю численность студентов в академической группе в апреле, если 1-20 апреля в состав студенческой группы входило 20 человек, а с 21 и до конца месяца – 24 человека.

ӱ=20+20+24*10/30=21

Средний абсолютный прирост – разница между последним и первым уровнем, деленная на n-1.

∆ӱ=(yn-y0)/(n-1)

Средний абсолютный прирост можно рассчитать по цепным абсолютным приростам. В этом случае он рассчитывается как отношение суммы цепных абсолютных приростов к их количеству.

∆ӱ=(Σ∆yцеп._i)/ n

Основываясь на взаимосвязи между цепными и базисными абсолютными приростами, показатель среднего абсолютного прироста рассчитывается как отношение базисного последнего прироста к n-1.

∆ӱ=(∆yбап)/(n-1)

Средний темп роста – обобщающая характеристика индивидуальных цепных темпов роста.

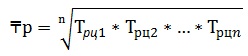
По абсолютным уровням ряда средний темп роста:

На условии взаимосвязи между цепными показателями, средний темп роста может быть вычислен по формуле:

Средний темп прироста - рассчитывается как разность между средним темпом роста и 100* или 1.

₸пр=₸р-100% или ₸пр=₸р-1

Дата добавления: 2015-04-23