Вероятностный подход к измерению информации

Подходы к измерению информации. Преимущества и недостатки вероятностного и алфавитного подходов к измерению информации. Единицы измерения информации. Скорость передачи информации. Пропускная способность канала связи

Информация является важнейшим понятием и основным объектом изучения в информатике (см. билет № 1). Неудивительно поэтому, что проблема измерения информации имеет фундаментальное значение1.

На бытовом уровне информация является синонимом слов сведения, знания, данные, новость, известие, сообщение и аналогичным им. При этом неявно подразумевается, что тот, кто получает информацию, выделяет из нее некоторый смысл (содержание).

Смысловая составляющая информации во многом индивидуальна. Большинство россиян не способны извлечь никакой информации из текста на японском языке. Многие взрослые, взяв учебник для начальных классов, также не сочтут его заслуживающей своего внимания информацией, хотя, в отличие от предыдущего случая, понимают (слишком хорошо!), что там написано. Химика редко интересуют сообщения об археологических открытиях, а большая часть литераторов активно игнорирует любые сведения из области математики. Наконец, многие образованные люди не верят в статьи, опубликованные в бульварной прессе, заранее считая их недостоверными. Таким образом, информативность любых сведений и сообщений существенно зависит от воспринимающего их человека, его предыдущих знаний, опыта, интересов, отношения к источнику информации и множества других факторов личного характера, т.е. по своей сути является субъективной.

Дополнительное пояснение. Во всех наиболее распространенных школьных учебниках подобными описаниями и несколькими несвязанными примерами неинформативных сообщений дело и ограничивается. Но на самом деле вопрос о соотношении между информативностью и предыдущими знаниями человека имеет самостоятельное значение. Например, в недавно вышедших учебниках [1, 2] приведен следующий весьма наглядный и любопытный качественный график зависимости воспринимаемой пользователем информации I от предварительно известных ему сведений S (для обозначения совокупности сведений, которыми располагает пользователь или любая другая система, принят специальный научный термин — тезаурус).

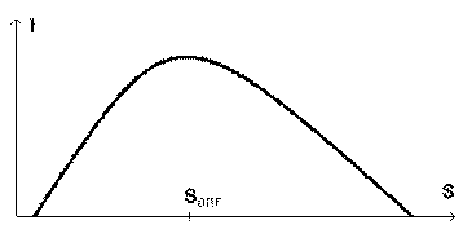
Из графика отчетливо видно, что воспринимаемая из фиксированного сообщения информация зависит от познаний пользователя неоднозначно. При малых S (тезаурус мал, пользователь неквалифицирован) воспринимаемая информация близка к нулю — человек ее просто не понимает. По мере роста S ситуация улучшается, и количество воспринятой из данного сообщения информации растет (невежественный пользователь быстро прогрессирует). Но лишь до определенного предела, а затем величина I начинает постепенно уменьшаться. Здесь вступает в действие другой фактор: при больших S (большой объем знаний, мы имеем дело с образованным пользователем) многие сообщения не могут добавить к тезаурусу ничего нового и их информативность вновь устремляется к нулю. Выражаясь житейским языком, когда человек много знает, его ничем не удивишь.

Таким образом, график количества воспринимаемой информации имеет максимум (на рисунке он обозначен S опт), соответствующий вполне определенному соотношению между содержащейся в сообщении информацией и уже имеющимися у субъекта знаниями2.

Если задуматься над сутью рассмотренного графика, то можно получить целый ряд практически интересных выводов. Например, что передаваемая информация должна определенным образом соотноситься с уже имеющимися в ее приемнике сведениями, иначе данные могут оказаться бесполезными и только напрасно будут загружать каналы связи и узлы обработки. Между прочим, учащиеся после этих рассуждений должны проникнуться еще большим уважением к учителю, который постоянно вынужден “подстраивать” степень информативности своего рассказа, интуитивно оценивая разнообразные объемы тезаурусов сидящих в классе учеников, причем с учетом возможности их интеллектуального роста по мере освоения материала.

Несколько иная трактовка измерения смысла сообщений по способу А.Н. Колмогорова весьма просто и интересно обсуждается в школьном учебнике [3].

Таким образом, субъективный характер восприятия информации делает однозначное измерение количества информации весьма затруднительным. Заметим, что современным компьютерам смысл обрабатываемых данных вообще принципиально недоступен, что делает еще более призрачной надежду на решение проблемы автоматического измерения “количества” содержания, которое в этих данных заключено.

Как же все-таки измерить информацию? Общепринятым на данный момент решением проблемы является измерение объема информации при полном игнорировании ее смысла. Такой подход, несмотря на кажущуюся бессмысленность, оказывается необычайно полезным и широко применяется на практике.

Действительно, в целом ряде важных практических задач смысл информации и даже ее вид (числа, текст, видео) несущественен. Например, при передаче информации по каналам связи, при распределении объемов ОЗУ для хранения различных типов данных, при записи информации на внешние носители, при архивации и многих других компьютерных применениях содержание передаваемой и обрабатываемой информации особого значения не имеет.

Нечто похожее наблюдается и в “некомпьютерных” областях. Так, книги хранятся и ищутся не по содержанию, а по другим, часто весьма формальным признакам; в библиотеке нашего университета, в частности, книги расставлены на стеллажах в том числе с учетом размера обложки, который явно слабо связан с содержанием книги. Аналогично почтальону должно быть все равно, что именно находится внутри доставляемого им конверта, а диктор телевидения не может пропускать отдельные новости или их фрагменты в соответствии со своими личными убеждениями.

Примечание. Подобно тому, как в физике при полном игнорировании трения можно установить фундаментальные законы движения, можно надеяться, что изучение “информации без смысла” позволит понять наиболее важные закономерности протекания информационных процессов.

На этих и многочисленных подобных примерах мы видим, что информация перестает зависеть от человека при абстрагировании от ее смысла. Следовательно, появляется возможность объективного измерения количества информации. При этом используется два подхода: вероятностный или алфавитный.

Любая информация может рассматриваться как уменьшение неопределенности наших знаний об окружающем мире (в теории информации принято говорить именно об уменьшении неопределенности, а не об увеличении объема знаний). Математически это высказывание эквивалентно простой формуле

I = H 1 – H 2

где I — это количество информации, а H 1 и H 2 — начальная и конечная неопределенность соответственно (очевидно, что H 1 l H 2). Величину H, которая описывает степень неопределенности, в литературе принято называть энтропи R ей.

Важным частным случаем является ситуация, когда некоторое событие с несколькими возможными исходами уже произошло, а, значит, неопределенность его результата исчезла. Тогда H 2 = 0 и формула для информации упрощается:

I = H

Таким образом, энтропия опыта равна той информации, которую мы получаем в результате его осуществления. И наоборот: информация, получаемая из опыта, может быть вычислена через его энтропию. Очевидно, что единицы измерения информации и энтропии совпадают.

Вычисление энтропии при вероятностном подходе базируется на рассмотрении данных о результате некоторого случайного события, т.е. события, которое может иметь несколько исходов. Случайность события заключается в том, что реализация того или иного исхода имеет некоторую степень неопределенности.

Пусть, например, абсолютно незнакомый нам ученик сдает экзамен, результатом которого может служить получение оценок 2, 3, 4 или 5. Поскольку мы ничего не знаем о данном ученике, то степень неопределенности всех перечисленных результатов сдачи экзамена совершенно одинакова. Напротив, если нам известно, как он учится, то уверенность в некоторых исходах будет больше, чем в других: так, отличник скорее всего сдаст экзамен на пятерку, а получение двойки для него — это нечто почти невероятное.

Наиболее просто определить количество информации в случае, когда все исходы события могут реализоваться с равной долей вероятности. В этом случае для вычисления информации используется формула Хартли. В более сложной ситуации, когда исходы события ожидаются с разной степенью уверенности, требуются более сложные вычисления по формуле Шеннона, которую обычно выносят за рамки школьного курса информатики. Очевидно, что формула Хартли является некоторым частным случаем более общей формулы Шеннона.

Формула Хартли была предложена в 1928 году американским инженером Р.Хартли. Она связывает количество равновероятных состояний N с количеством информации I в сообщении о том, что любое из этих состояний реализовалось. Наиболее простая форма для данной формулы записывается следующим образом:

2 I = N

Причем обычно значение N известно, а I приходится подбирать, что не совсем удобно. Поэтому те, кто знает математику получше, предпочитают преобразовать данную формулу так, чтобы сразу выразить искомую величину I в явном виде:

I = log2 N

Важный частный случай получается из приведенной формулы при N = 2, когда результатом вычисления является единичное значение. Единица информации носит название бит (от англ. BI nary digi T — двоичная цифра); таким образом, 1 бит — это информация о результате опыта с двумя равновероятными исходами. Чем больше возможных исходов, тем больше информации в сообщении о реализации одного из них.

Пример 1. Из колоды выбрали 16 карт (все “картинки” и тузы) и положили на стол рисунком вниз. Верхнюю карту перевернули (см. рисунок). Сколько информации будет заключено в сообщении о том, какая именно карта оказалась сверху?

Все карты одинаковы, поэтому любая из них могла быть перевернута с одинаковой вероятностью. В таких условиях применима формула Хартли.

Событие, заключающееся в открытии верхней карты, для нашего случая могло иметь 16 возможных исходов. Следовательно, информация о реализации одного из них равняется

I = log2 16 = 4 бита

Примечание. Если вы не любите логарифмы, можно записать формулу Хартли в виде 2 I = 16 и получить ответ, подбирая такое I, которое ей удовлетворяет.

Пример 2. Решите предыдущую задачу для случая, когда сообщение об исходе случайного события было следующим: “верхняя перевернутая карта оказалась черной дамой”.

Отличие данной задачи от предыдущей заключается в том, что в результате сообщения об исходе случайного события не наступает полной определенности: выбранная карта может иметь одну из двух черных мастей.
В этом случае, прежде чем воспользоваться формулой Хартли, необходимо вспомнить, что информация есть уменьшение неопределенности знаний:

I = H 1 – H 2

До переворота карты неопределенность (энтропия) составляла

H 1 = log2 N 1

после него —

H 2 = log2 N 2

(причем для нашей задачи N 1 = 16, а N 2 = 2).

В итоге информация вычисляется следующим образом:

I = H 1 – H 2 = log2 N 1 – log2 N 2 = log2 N 1/ N 2 = log2 16/2 = 3 бита

Заметим, что в случае, когда нам называют карту точно (см. предыдущий пример), неопределенность результата исчезает, N 2 = 1, и мы получаем “традиционную” формулу Хартли. И еще одно полезное наблюдение. Полная информация о результате рассматриваемого опыта составляет 4 бита (см. пример 1). В данном же случае мы получили 3 бита информации, а оставшийся четвертый описывает сохранившуюся неопределенность выбора между двумя дамами черной масти.

Дата добавления: 2015-04-23