Алфавитный (объемный) подход к измерению информации

Помимо описанного выше вероятностного подхода к измерению информации, состоящего в подсчете неопределенности исходов того или иного события, существует и другой. Его часто называют объемным, и он заключается в определении количества информации в каждом из знаков дискретного сообщения с последующим подсчетом количества этих знаков в сообщении.

Пусть сообщение кодируется с помощью некоторого набора знаков. Заметим, что если для данного набора установлен порядок следования знаков, то он называется алфавитом. Наиболее сложной частью работы при объемном измерении информации является определение количества информации, содержащейся в каждом отдельном символе: остальная часть процедуры весьма проста. Для определения информации в одном символе алфавита можно также использовать вероятностные методы, поскольку появление конкретного знака в конкретном месте текста есть явление случайное.

Самый простой метод подсчета заключается в следующем. Пусть алфавит, с помощью которого записываются все сообщения, состоит из M символов. Для простоты предположим, что все они появляются в тексте с одинаковой вероятностью (конечно, это грубая модель3, но зато очень простая). Тогда в рассматриваемой постановке применима формула Хартли для вычисления информации об одном из исходов события (о появлении любого символа алфавита):

I = log2 M

Поскольку все символы “равноправны”, естественно, что объем информации в каждом из них одинаков. Следовательно, остается полученное значение I умножить на количество символов в сообщении, и мы получим общий объем информации в нем. Напомним читателям, что осмысленность сообщения в описанной процедуре нигде не требуется, напротив, именно при отсутствии смысла предположение о равновероятном появлении всех символов выполняется лучше всего!

Примечание. Стоит знать, что описанный простой способ кодирования, когда коды всех символов имеют одинаковую длину, не является единственным. Часто при передаче или архивации информации по соображениям экономичности тем символам, которые встречаются чаще, ставятся в соответствие более короткие коды и наоборот. Мы здесь не будем рассматривать этот весьма интересный и практически важный вопрос. Желающие могут обратиться, например, к известному школьному учебнику информатики [4] (начиная со второго издания) или к более глубокому, но тоже достаточно понятному [5].

Можно показать, что при любом варианте кодирования

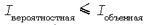
(чем экономичнее способ кодирования, тем меньше разница между этими величинами — см. пример 4, приведенный ниже).

Пример 3. Определить информацию, которую несет в себе 1-й символ в кодировках ASCII и Unicode.

В алфавите ASCII предусмотрено 256 различных символов, т.е. M = 256, а

I = log2 256 = 8 бит = 1 байт

В современной кодировке Unicode заложено гораздо большее количество символов. В ней определено 256 алфавитных страниц по 256 символов в каждой. Предполагая для простоты, что все символы используются, получим, что

I = log2 (256 * 256) = 8 + 8 = 16 бит = 2 байта

Пример 4. Текст, сохраненный в коде ASCII, состоит исключительно из арифметических примеров, которые записаны с помощью 10 цифр от 0 до 9, 4 знаков арифметических операций, знака равенства и некоторого служебного кода, разделяющего примеры между собой. Сравните количество информации, которое несет один символ такого текста, применяя вероятностный и алфавитный подходы.

Легко подсчитать, что всего рассматриваемый в задаче текст состоит из N = 16 различных символов. Следовательно, по формуле Хартли

I _{вероятностная} = log2 16 = 4 бита

В то же время, согласно вычислениям примера 3, для символа ASCII

I _{алфавитная} = 8 бит

Двукратный избыток при кодировании символов связан с тем, что далеко не все коды ASCII оказываются в нашем тексте востребованными. В то же время несложно построить вариант специализированной 4-битной кодировки для конкретной задачи4, для которого I вероятностная и I алфавитная окажутся равными.

В порядке подведения итогов сравним вероятностный и алфавитный подходы, как того требует вопрос билета. Первый подход позволяет вычислить предельное (минимально возможное) теоретическое значение количества информации, которое несет сообщение о данном исходе события. Второй — каково количество информации на практике с учетом конкретной выбранной кодировки. Очевидно, что первая величина есть однозначная характеристика рассматриваемого события, тогда как вторая зависит еще и от способа кодирования: в “идеальном” случае обе величины совпадают, однако на практике используемый метод кодирования может иметь ту или иную степень избыточности.
С рассмотренной точки зрения вероятностный подход имеет преимущество. Но, с другой стороны, алфавитный способ заметно проще и с некоторых позиций (например, для подсчета требуемого количества памяти) полезнее.

Примечание. В учебниках информатики обычно ограничиваются описанием обоих подходов и не производится их сравнение. Приведенное выше сопоставление авторы провели исходя из собственных представлений. Возможно, составители билетов имели в виду какие-либо еще преимущества и недостатки.

Вопрос о единицах измерения информации уже возникал при обсуждении вероятностного и алфавитного подходов. В самом деле, трудно изложить способ измерения величины, не упоминая при этом о единицах ее измерения. Поэтому мы уже сформулировали выше, что с теоретической точки зрения 1 бит — это информация, которая сокращает неопределенность наших знаний вдвое (ответ на вопрос типа “да”/“нет”, наличие или отсутствие какого-либо свойства, четность числа и т.д.). С точки зрения практической реализации компьютерных устройств для обработки информации 1 бит — это отдельный двоичный разряд любого из таких устройств. Иначе говоря, в вычислительной технике бит служит конструктивной базой для построения всех цифровых двоичных устройств: регистров, сумматоров и т.п. Отсюда очевидно, что в теории информации количество бит может быть любым, в том числе дробным, в то время как в реальных устройствах оно обязательно целое.

Бит, будучи минимально возможной порцией информации в компьютере, довольно маленькая единица измерения. Поэтому на практике чаще всего используется другая единица, которая называется 1 байт =
8 бит. С точки зрения устройства компьютера байт замечателен тем, что является минимальной адресуемой информацией в компьютере, иначе говоря, считать из памяти часть байта невозможно. В современных компьютерах все устройства памяти имеют байтовую структуру, а внешние устройства также обмениваются информацией байтами или кратными ему порциями. Как следствие все типы данных (числа, символы и др.) представляются в компьютере величинами, кратными байту.

Примечание. Даже логические переменные, для каждой из которых, казалось бы, достаточно 1 бита, обычно занимают в оперативной памяти полный байт (или иногда ради единообразия даже несколько байт, например, LongBool в Паскале).

С целью получения шкалы для измерения объемов информации в широких пределах от байта с помощью стандартных приставок образуется целая система более крупных производных единиц:

1 килобайт = 1024 байта

1 мегабайт = 1024 килобайта

1 гигабайт = 1024 мегабайта

и т.д. В отличие от общепринятой системы производных единиц (широко используемой, например, в физике) при пересчете применяется множитель 1024, а не 1000. Причина заключается в двоичном характере представления информации в компьютере: 1024 = 210, и, следовательно, лучше подходит к измерению двоичной информации.

Научившись измерять количество информации, можно ставить вопрос, как быстро она передается. Величину, которая равна количеству информации, передаваемому за единицу времени, принято называть скоростью передачи информации. Очевидно, что если за время t по каналу связи передано количество информации I, то скорость передачи вычисляется как отношение I / t.

Примечание. При практической работе с величиной скорости передачи информации следует очень внимательно относиться к тому, что именно понимается под передаваемой информацией I. В частности, в процессе передачи к собственно пользовательской информации может добавляться значительное количество служебных, вспомогательных данных: например, согласно сетевому протоколу UDP (U ser D atagram P rotocol), который является некоторой разновидностью известного протокола TCP (T ransmission C ontrol P rotocol), из 146 байт стандартного Ethernet-кадра 46 являются служебными [6]. Кроме того, непосредственно перед передачей данные могут сжиматься или шифроваться, что также повлияет на время их передачи.

Скорость передачи данных нельзя сделать сколь угодно большой; ее предельная максимальная величина имеет специальное название — пропускная способность канала связи. Данная характеристика определяется устройством канала и, что не так очевидно, способом передачи сигналов по нему. Иными словами, для разных способов представления данных одна и та же линия связи может иметь разную пропускную способность.

К.Шеннон в созданной им теории информации доказал, что достигнуть при передаче пропускной способности линии можно всегда и путем к этому является повышение эффективности кодирования. Более того, даже при наличии в канале шумов любого уровня всегда можно закодировать сообщение таким образом, чтобы не происходило потери информации [1, 5].

Обе величины — скорость передачи и пропускная способность — по определению измеряются в одних и тех же единицах, являющихся отношением единиц информации и времени: бит/с, байт/с, Кб/с и т.д.

Дополнительное пояснение. Кроме того, существует еще одна родственная единица измерения параметров передачи — бод. Количество бод есть количество изменений информационного параметра в секунду. Скорость передачи в битах в секунду в общем случае не совпадает с количеством бод. В [1] приводится очень наглядный пример, когда скорость в бит/с втрое выше, чем число бод. “Если информационными параметрами являются фаза и амплитуда синусоиды, причем различают 4 состояния фазы (0, 90, 180 и 270) и два значения амплитуды, то информационный сигнал имеет восемь различимых состояний. В этом случае модем, работающий со скоростью 2400 бод (с тактовой частотой 2400 Гц), передает информацию со скоростью 7200 бит/с, так как при одном изменении сигнала передается три бита информации”. Возможно, кстати, и обратное соотношение между величинами в бит/с и бод; в частном случае они могут совпадать.

В качестве примера типичных значений скоростей передачи данных в современных компьютерах ниже приводятся табл. 1 и 2, составленные на основе сведений из известной книги [7].

Таблица 1. Характеристики устройств внешней памяти

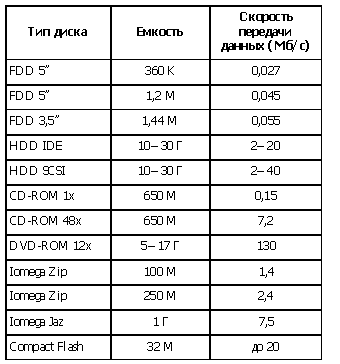
Таблица 2. Характеристики шин расширения

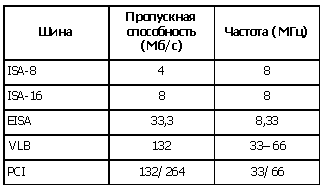
Примечание. Хотя проблема пропускной способности каналов связи весьма подробно излагается в специальной литературе, в доступных для учителей и школьников источниках она рассматривается не всегда, а если и рассматривается, то весьма поверхностно. Поэтому на экзамене, по мнению авторов, надо требовать от учеников знания только самых минимальных сведений. Расширенный материал в нашей публикации приведен исключительно для того, чтобы дать некоторую общую ориентировку учителям. Нам кажется, что это один из примеров, когда, прежде чем требовать знания вопроса от учащихся, стоит описать его на нужном уровне в школьных учебниках.

Литература

1. Акулов О.А., Медведев Н.В. Информатика: базовый курс. М.: Омега-Л, 2005, 552 с.

2. Бройдо Э.А., Ильина О.П. Архитектура ЭВМ и систем. СПб.: Питер, 2006, 718 с.

3. Информационная культура: Кодирование информации, информационные модели. 9–10-е классы. М.: Дрофа, 2000, 208 с.

4. Семакин И.Г. Информатика. Базовый курс. 7–9-е классы / И.Г. Семакин, Л.А. Залогова, С.В. Русаков, Л.В. Шестакова. 2-е изд. М.: БИНОМ, 2004, 390 с.

5. Стариченко Б.Е. Теоретические основы информатики. М.: Горячая линия — Телеком, 2003, 312 с.

6. Никифоров С.В. Введение в сетевые технологии. М.: Финансы и статистика, 2003, 224 с.

7. Аппаратные средства IBM PC. Энциклопедия. / М.Гук. СПб.: Питер, 2003, 923 с.

Дата добавления: 2015-04-23