Законы распределения вероятности безотказной работы

Вероятность безотказной работы.

Поскольку в теории надежности отказ является событием случайным, то для его описания использую случайную величину 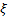- время наработки до первого отказа.

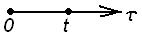
0 – момент включения устройства; t – время проведения измерений на наличие отказов.

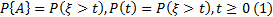, событие А: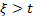

P(t) – вероятность безотказной работы – основная характеристика безотказности, представляющая собой вероятность того, что время наработки будет превышать заданный интервал от 0 до t.

t->0 => P(t)->1; t->беск. =>P(t)->0

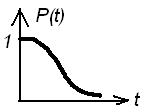
Распределение Вейбулла.

Двухпараметрическое экспоненциальное распределение Вейбулла используется для описания вероятности безотказной работы P(t)

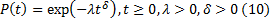
Воспользуемся 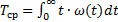найдем плотность вероятностей момента первого отказа:

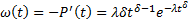
Найдем интенсивность отказа:

(11) – соотношение для описания интенсивности отказа в распределении Вейбулла, где 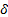- параметр формы.

1) 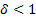, то 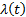уменьшается, соответствует интервалу приработки

2) 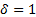, то 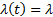, соответствует этапу эксплуатации системы

3) 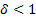, то 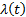возрастает, соответствует этапу износа конструкции.

Экспоненциальное распределение.

Экспоненциальное распределение вероятности безотказной работы является частным случаем распределения Вейбулла при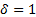

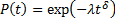
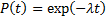
Определяется одним параметром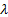

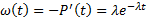
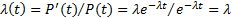
Экспоненциальное распределение позволяет описать вероятность безотказной работы на этапе эксплуатации системы. Для экспоненциального распределения .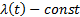

Найдем для экспоненциального распределения среднее время наработки до первого отказа используя соотношение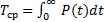

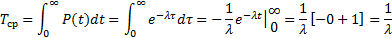
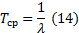
Для экспоненциального распределения среднее время наработки и интенсивность отказа связаны зависимостью (14). 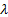[1/час] [кол-во отказов/час].

Особенности экспоненциального распределения.

Из соотношения 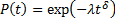, учтя 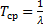, получим . .

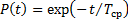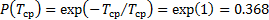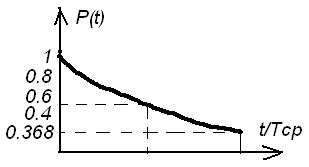
Для экспоненциального распределения время нормальной эксплуатации меньше среднего времени наработки до первого отказа. Найдем для экспоненциального распределения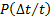

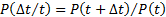
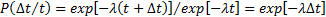
Учитывая вероятность безотказной работы 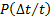на интервале 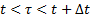определяется лишь длиной интервала и не зависит от начала отсчета, т.е. t может иметь любые значения.

Экспоненциальное распределение не учитывает фактор старения, оно является идеализированной моделью, которая лишь с некоторым приближением позволяет оценить вероятность появления внезапных отказов, поэтому экспоненциальное распределение используется в основном в априорной теории надежности для сравнительной оценки разрабатываемых/проектируемых вариантов технических решений.

Основное достоинство – простота расчетов. Использование экспоненциального распределения в апостериорной теории надежности возможно лишь при проверке результатами испытаний данных полученных при использовании экспоненциальных распределений.

Дата добавления: 2015-04-23