Пример. Групповой подход к геометрии

Групповой подход к геометрии. Применение многомерных пространств

Определение. Центроаффинным преобразованием с центром S называетсяаффинное преобразование оставляющее неподвижной точку S.

Теорема 123. Каждая из множеств всех: аффинных преобразований, центроаффинных преобразований, преобразование движения, образуют группу.

Во второй половине XIX века немецкий математик Феликс Клей определил геометрию, как науку о свойствах фигур, которые остаются неизменными при преобразованиях некоторой группы.

Каждой группе преобразований соответствует своя геометрия, следовательно в зависимости от разных преобразований, можно построить много разных геометрий.

1. Группа аффинных преобразований соответствует аффинной геометрии, изучающей свойства фигур неизменных при аффинном преобразовании.

2. Группа центроаффинного преобразования, соответствует центроаффинной геометрии.

3. Группе движений соответствует евклидова геометрия.

Для пространств 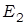и 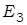эта геометрия совпадает с элементарной геометрией, изучающейся в средней школе (точнее, элементарная геометрия, объединяет геометрии соответствующие группе движения и группе подобия).

Можно также рассматривать геометрию, изучающую свойства фигур, которые не меняются при следующих преобразованиях.

1. Вращение (поворот).

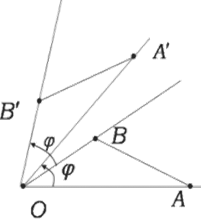
Рис. 1

2. Параллельный перенос.

Рис.2

3. Осевая симметрия.

Рис.3

4. Скользящая симметрия.

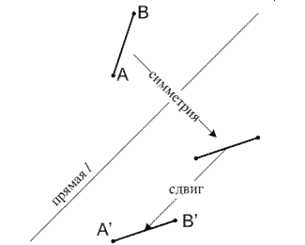
Рис.4

И т.д.

Замечание. Свойства фигур, сохраняющиеся при всех преобразованиях данной группы, сохраняются в частности и при преобразованиях некоторой ее подгруппы. Обратное же неверно: свойства фигур, сохраняющиеся при преобразованиях подгруппы (поворот) необязательно сохраняются при преобразованиях всей группы (движения).

Вывод. Геометрия, соответствующая подгруппе чаще всего «богаче» по содержанию, чем геометрия всей группы (евклидова геометрия богаче, чем аффинная геометрия).

Схема подгрупп различных групп описанных выше геометрии

Замечание. Чем ниже находится группа в данной схеме, тем «богаче» ее геометрия.

Пример. Теорема Пифагора справедлива в школьной геометрии, но она не выполняется в аффинной геометрии.

Многомерные пространства могут быть применены в различных областях науки.

Пример 1. Рассмотрим сеть проводников постоянного тока, состоящую из n однородных проволок с силой тока в них соответственно 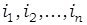, тогда состояние системы в любой момент времени – точка n-мерного евклидового пространства.

Начало координат точка O(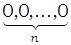), соответствует состоянию системы без тока. Расстояние от 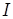(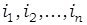) от точки O есть: 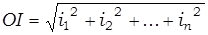, последнее означает количество теплоты выделяемой данной системой проводников.

Пример 2. Следующие величины могут быть рассмотрены как координаты точек n-мерного пространства.

а) (ct, ) – координаты точки в четырехмерном пространстве, здесь c – скорость света, t – время, - координаты объекта.

б) в качестве координат используют три цвета электронно-лучевой трубки (синий, зеленый, красный) – трехмерное пространство.

в) состояние вещества в замкнутом сосуде – две величины (давление, температура).

Дата добавления: 2015-04-23