Евклидовы пространства

. Для развития геометрических методов в теории В. п. нужно указать пути обобщения таких понятий, как длина вектора, угол между векторами и т.п. Один из возможных путей заключается в том, что любым двум векторам х и у из R ставится в соответствие число, обозначаемое (х, у) и называемое скалярным произведением векторов х и у. При этом требуется, чтобы выполнялись следующие аксиомы скалярного произведения:

1) (х, у)=(у, х) (перестановочность);

2) (x₁ + x₂, y)=(x₁, y)+(x₂, y) (распределительное свойство);

3) (x, у)=  (х, у),

4) (х, х)  0 для любого х, причем (х, х) = 0 только для х = 0.

Обычное скалярное произведение в трёхмерном пространстве этим аксиомам удовлетворяет. В. п., в котором определено скалярное произведение, удовлетворяющее перечисленным аксиомам, называется евклидовым пространством; оно может быть как конечномерным (n-мерным), так и бесконечномерным. Бесконечномерное евклидово пространство обычно называют гильбертовым пространством. Длина | x | вектора x и угол между векторами х и у евклидова пространства определяются через скалярное произведение формулами

Примером евклидова пространства может служить обычное трёхмерное пространство со скалярным произведением, определяемым в векторном исчислении. Евклидово n-мepное (арифметическое) пространство Eⁿ получим, определяя в n -мepном арифметическом В. п. скалярное произведение векторов x =(₁, …, _n) и y = (₁, …, _n) соотношением

(x, y)= ₁₁ + ₂₂ + … + _n_n. (2)

При этом требования 1)—4), очевидно, выполняются.

В евклидовых пространствах вводится понятие ортогональных (перпендикулярных) векторов. Именно векторы х и у называются ортогональными, если их скалярное произведение равно нулю: (х, у)= 0. В рассмотренном пространстве Eⁿ условие ортогональности векторов x =(₁, …, _n) и y =(₁, …, _n), как это следует из соотношения (2), имеет вид:

₁₁ + ₂₂ + … + _n_n = 0. (3)

Применение В. п. Понятие В. п. (и различные обобщения) широко применяется в математике и её приложениях к естествознанию. Пусть, например, R — множество всех решений линейного однородного дифференциального уравнения yⁿ + a₁ (x) y ^{(n + 1)} + … + a_n (x) y = 0. Ясно, что сумма двух решений и произведение решения на число являются решениями этого уравнения. Таким образом, R удовлетворяет условиям А. Доказывается, что для R выполнено обобщённое условие В. Следовательно, R является В. п. Любой базис в рассмотренном В. п. называется фундаментальной системой решений, знание которой позволяет найти все решения рассматриваемого уравнения. Понятие евклидова пространства позволяет полностью геометризовать теорию систем однородных линейных уравнений:

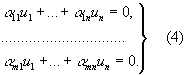
Рассмотрим в евклидовом пространстве Eⁿ векторы a_i =(_i1, _i2, …, _in), i = 1, 2,..., n и вектор-решение u =(u₁, u₂,..., u_n).Пользуясь формулой (2) для скалярного произведения векторов Eⁿ, придадим системе (4) следующий вид:

(a_i, u)= 0, i = 1, 2, …, m. (5)

Из соотношений (5) и формулы (3) следует, что вектор-решение u ортогонален всем векторам a_i. Иными словами, этот вектор ортогонален линейной оболочке векторов a_i, то есть решение u есть любой вектор из ортогонального дополнения линейной оболочки векторов a_i. Важную роль в математике и физике играют и бесконечномерные линейные пространства. Примером такого пространства может служить пространство С непрерывных функций на отрезке с обычной операцией сложения и умножения на действительные числа. Упомянутое выше пространство всех многочленов является подпространством пространства С.

Дата добавления: 2015-04-23