Аффинные преобразования пространства

Аффинные преобразования пространства.

Преобразование подобия пространства

Определение. Аффинным преобразованием пространства называется преобразование пространства, переводящее каждую плоскость в плоскость.

Свойства.

1.
При аффинном преобразовании прямые переходят в прямые.

2.
Аффинное преобразование пространства индуцирует аффинное отображение каждой плоскости на её образ.

3.
При аффинном преобразовании параллельные плоскости (прямые) переходят в параллельные плоскости (прямые).

Доказательства свойств.

1.
Следует из того, что прямая есть пересечение двух плоскостей, и из определения аффинного преобразования.

2.
Следует из определения аффинного преобразования и свойства 1.

3.
Для плоскостей доказывается от противного, для прямых – через свойство 2 и свойство аффинного преобразования плоскости.

Теорема 3.1. (о задании аффинного преобразования пространства) Для любых данных тетраэдров АВСD и А´В´С´D´ существует единственное аффинное преобразование, переводящее А в А´, В в В´, С в С´, D в D´.

Доказательство. Доказывается аналогично теореме 1.1. (строятся решётки параллелепипедов).

Из доказательства теоремы 3.1 следует, что если у нас есть некоторая косоугольная система координат W, а W´ – её образ при аффинном преобразовании, то координаты произвольной точки пространства в системе координат W равны координатам её образа в системе координат W´.

Отсюда сразу вытекают ещё некоторые свойства аффинного преобразования.

4.
Преобразование, обратное аффинному, является аффинным.

5.
Аффинные преобразования сохраняют отношения длин параллельных отрезков.

Теперь пусть в пространстве задана система координат (О, 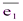, , 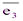) и аффинное преобразование f переводит О в О´ 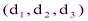, а базисные вектора в вектора , , соответственно. Найдём координаты x´, y´, z´ образа M´(x´,y´,z´) точки M(x,y,z) при преобразовании f.

Будем исходить из того, что точка М в системе координат (О, 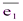, , 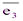) имеет такие же координаты, что и точка М´ в системе координат (О´, , , 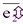). Отсюда

.

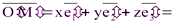
Поэтому имеем равенства (*):

Стоит ещё заметить, что 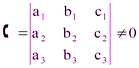, т.к. векторы , , 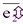линейно независимы.

Этот определитель называется определителем аффинного преобразования.

Теорема 3.2. Преобразование, заданное равенствами (*), при является аффинным.

Доказательство. Достаточно проверить, что преобразование, обратное преобразованию(*), является аффинным (свойство 4). Возьмём произвольную плоскость Аx´+Вy´+Сz´+D=0, где А, В, С не равны одновременно нулю. Выполняя подстановки (*), получим уравнение её прообраза:

.

Остаётся лишь проверить, что в полученном уравнении коэффициенты при x, y, z одновременно не равны нулю. Это действительно так, т.к. иначе система

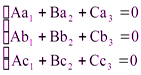
с неравным нулю определителем имела бы лишь нулевое решение: А=В=С=0, что неверно.

Теорема 3.3. Для объёмов V и V´ соответственных при аффинном преобразовании тел имеет место зависимость .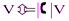

Доказательство. Пусть некомпланарные векторы , , 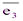образуют векторный базис пространства, и пусть в пространстве заданы векторы , и 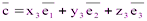. Вычислив смешанное произведение этих векторов, получим:

.

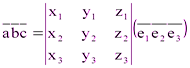Воспользуемся тем, что объём ориентированного параллелепипеда, построенного на векторах 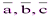как на рёбрах, равен смешанному произведению этих векторов:

,

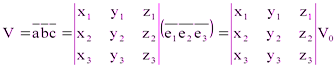где V₀ – объём параллелепипеда, построенного на базисных векторах.

Аффинное преобразование не изменяет координаты соответственных векторов в соответственных базисах. Поэтому для объёма V´ образа параллелепипеда объёма V имеем:

,

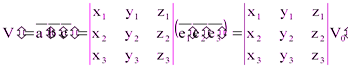где 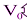– объём параллелепипеда, построенного на векторах , как на рёбрах.

Отсюда получаем: 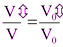. Далее , поэтому для неориентированных объёмов имеем . На все тела это равенство можно распространить аналогично доказательству свойства 4 подобий (часть II, §2).

Задача.

Вершина параллелепипеда соединена с центрами трёх не содержащих её граней. Найдите отношение объёма полученного тетраэдра к объёму данного параллелепипеда.

Решение.

Посчитаем данное отношение для куба и, переведя аффинным преобразованием куб в параллелепипед, воспользуемся тем, что аффинное преобразование сохраняет отношение объёмов. Для куба отношение легко считается. Оно равно 1:12.

Ответ: 1:12.

Дата добавления: 2015-04-23