Виды проецирования

Аффинные преобразования в пространстве

Для выполнения пространственных построений, аналогично двумерной задаче, три координаты точки (x, y, z) заменяются четверкой чисел (x, y, z, 1). Это дает возможность воспользоваться матричной записью и в более сложных трехмерных задачах.

Любое аффинное преобразование в трехмерном пространстве может быть представлено в виде суперпозиции вращений, растяжений, отражений и переносов. Математически все преобразования сводятся к перемножению матриц четвертого порядка. Например, матрица вращения вокруг оси абсцисс на угол j имеет вид:

.

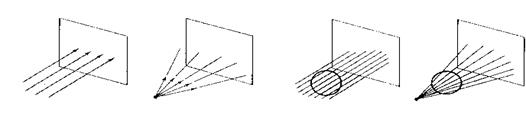
Изображение трехмерных объектов на картинной плоскости связано с еще одной геометрической операцией – проецированием при помощи пучка прямых.

В компьютерной графике применяется несколько различных видов проецирования. Наиболее часто используется параллельное и центральное проецирование.

Для получения проекций объекта на картинную плоскость необходимо провести через каждую его точку прямую из заданного проецирующего пучка и затем найти координаты точки пересечения этой прямой с плоскостью изображения. В случае центрального проецирования все прямые исходят из одной точки – центра пучка. При параллельном проецировании считается, что центр пучка расположен в бесконечности (рис. 4). Математически операция проецирования также сводится к перемножению соответствующих матриц.

Рис. 4

35. Движение (в геометрии)

Движение в геометрии, преобразования пространства, сохраняющие свойства фигур (размеры, форму и др.) Понятие Д. сформировалось путем абстракции реальных перемещении твердых тел. Д. евклидова пространства — геометрическое преобразованиепространства, сохраняющее расстояния между точками. Д. называют собственным или несобственным в зависимости от того, сохраняет ли оно или меняет ориентацию, Д. есть ортогональное преобразование.

Собственное Д. на плоскости можетбыть задано в прямоугольной системе координат (х, у) посредством следующих формул:

х; = xcosj — ysinj + a,

у; = xsinj + ycosj + b,

показывающих, что совокупность всех собственных Д. на плоскости зависит от трёх параметров а, b и j, которые характеризуют соответственно параллельный перенос плоскости на вектор (а, b) и её поворот вокруг начала координат на угол j. Всякое собственное Д. может быть представлено либо как параллельный перенос, либо как вращение вокруг некоторой точки. Любое несобственное Д. представимо в виде произведения (последовательного осуществления) параллельного переноса вдоль некоторого направления и симметрии относительно прямой, имеющей то же самое направление. Собственное Д. в пространстве есть или вращение вокруг оси, или параллельный перенос, или же может быть представлено в виде винтового движения (вращения вокруг оси и параллельного переноса в направлении этой оси).

Несобственное Д. в пространстве есть либо симметрия относительно плоскости, либо может быть представлено в виде произведения симметрии относительно плоскости на вращение вокруг оси, перпендикулярной этой плоскости, либо в виде произведения симметрии относительно плоскости на перенос в направлении вектора, параллельного этой плоскости, Д. в пространстве аналитически может быть представлено посредством линейного преобразования с ортогональной матрицей, определитель которой равен 1 или -1, в зависимости от того, является Д. собственным или несобственным, Понятие Д. переносится в римановы пространства, в пространства аффинной связности. Важную роль понятие Д. играет в римановых пространствах теории относительности (сильная асимметрия гравитационных полей накладывает ограничения на движения твёрдых тел в таких пространствах). Д. может быть принято в качестве основного понятия при аксиоматическом построении геометрии. В этом случае вместо аксиом конгруэнтности вводятся аксиомы Д. Конгруэнтность отрезков, углов и др. фигур определяется через понятие Д. (фигуры называются конгруэнтными, если одна переходит в другую при помощи некоторого Д.). Совокупность Д. образует группу.

36. Два вида движений. Инвариантные точки, прямые и плоскости

37. Классификация движений пространства.
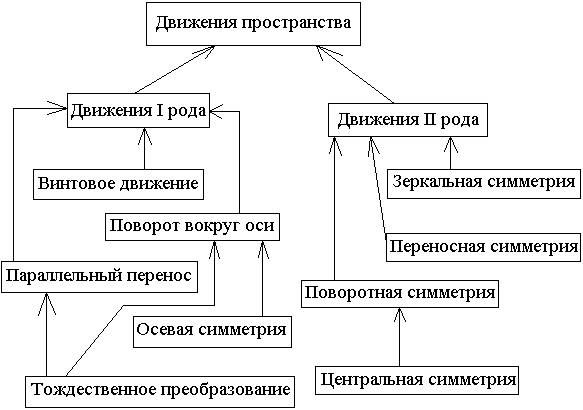
Теорема 7.0. Любое движение пространства есть параллельный перенос, винтовое движение, поворот вокруг оси, зеркальная симметрия, поворотная симметрия или переносная симметрия.

Для этого удобно разбить все движения по классам. И для каждого класса определить все движения, входящие в этот класс. Для начала разобьём все движения на движения I и II рода и докажем две теоремы, из которых сразу следует теорема 7.0:

Теорема 7.1. Любое движение I рода есть параллельный перенос, винтовое движение или поворот вокруг оси.

Теорема 7.2. Любое движение II рода – это зеркальная симметрия, поворотная симметрия или переносная симметрия.

Для доказательства этих теорем удобно разбить движения на классы по количеству неподвижных точек. Теперь мы получим четыре теоремы, каждая из которых в отдельности доказывается несложно:

Теорема 7.1.а. Любое движение I рода, имеющее хотя бы одну неподвижную точку, является поворотом вокруг оси.

Теорема 7.1.б. Любое движение I рода, не имеющее неподвижных точек, есть параллельный перенос или винтовое движение.

Теорема 7.2.а. Любое движение II рода, имеющее хотя бы одну неподвижную точку, является зеркальной симметрией или поворотной симметрией.

Теорема 7.2.б. Любое движение II рода, не имеющее неподвижных точек, есть переносная симметрия.

Эти теоремы фактически доказывают теоремы 7.1 и 7.2.

Будем доказывать их не по порядку, т.к. при доказательстве некоторых теорем удобно использовать другие.

Пусть f – данное движение.

Доказательство теоремы 7.1.а. Утверждение – простое следствие теоремы 6.5 (теоремы Даламбера), согласно которой f можно представить композицией двух зеркальных симметрий. Если плоскости симметрии параллельны, то f – параллельный перенос, что невозможно, т.к. у параллельного переноса нет неподвижных точек. Значит, плоскости симметрии пересекаются по некоторой прямой ℓ. Тогда, как легко показать, f – поворот вокруг оси ℓ на удвоенный ориентированный угол между плоскостями симметрии.

Доказательство теоремы 7.2.а. Возможны два случая: f – зеркальная симметрия или f – композиция трёх зеркальных симметрий (теорема 6.4). В первом случае и доказывать нечего. Во втором случае рассмотрим неподвижную точку О нашего преобразования f. Теперь рассмотрим движение 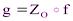. У движения g точка О неподвижная. С другой стороны, g – движение I рода (т.к. меняет ориентацию). Отсюда (теорема 7.1.а) g – поворот вокруг оси, содержащей точку О. Но 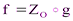, т.е. f – поворотная симметрия.

Доказательство теоремы 7.2.б. Пусть А´ – образ некоторой точки А при движении f, α – плоскость симметрии точек А и А´. Тогда движение первого рода имеет неподвижную точку А´. По теореме 7.1.а движение g – поворот вокруг оси. Пусть 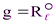. Тогда 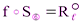, откуда , причём ℓ||α, иначе общая точка ℓ и α будет неподвижной точкой движения f. Как мы уже говорили, композицией двух зеркальных симметрий (если плоскости симметрий не параллельны) будет поворот вокруг общей прямой плоскостей симметрий на удвоенный ориентированный угол между плоскостями симметрий. Отсюда понятно, что поворот вокруг оси можно представить композицией двух зеркальных симметрий. Плоскости симметрий должны обе содержать ось поворота, причём одну из этих плоскостей в остальном можно выбрать произвольно. Представим , выбрав плоскость β перпендикулярной плоскости α. Тогда 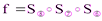. Заметим, что – осевая симметрия S_u, где . Причём u||γ, т.к. u параллельна прямой ℓ, лежащей в плоскости γ. S_u можно представить композицией двух зеркальных симметрий , где . При этом получится π||γ. Тогда , причём 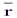– вектор, перпендикулярный плоскостям γ и π, т.е. ||σ. Таким образом, – переносная симметрия.

Доказательство теоремы 7.1.б. Опять возьмём произвольную точку А, её образ А´ при движении f и плоскость ω симметрии точек А и А´. Тогда движение 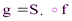второго рода имеет неподвижную точку А. По теореме 7.2.а движение g – зеркальная симметрия или поворотная симметрия.

Если g – зеркальная симметрия, то f является композицией двух зеркальных симметрий. Кроме того f не имеет неподвижных точек, т.е. f – параллельный перенос.

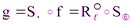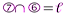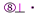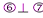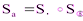Пусть теперь () – поворотная симметрия. Представим (), причём выберем . Тогда . Т.к. , , и – осевые симметрии. Итак, 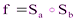– композиция двух осевых симметрий.

Если a и b пересекаются, то у f есть неподвижная точка, что невозможно.

Если a и b параллельны, то f, как легко убедиться, – параллельный перенос.

Если а и b скрещиваются, то рассмотрим их общий перпендикуляр h и прямую p такую, что p проходит через точку пересечения h и a и p||b. Тогда, как легко убедиться, 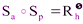– поворот вокруг прямой h на некоторый угол, а 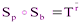– параллельный перенос на некоторый вектор 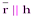. Поэтому 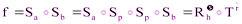– винтовое движение.

Пользуясь, полученными результатами получаем таблицу:

Дата добавления: 2015-04-23