Уравнения прямой на плоскости

Способы задания прямой:
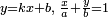или .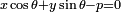

[править]Общее уравнение прямой

Общее уравнение прямой линии на плоскости в декартовых координатах:

где , 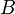и 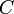— произвольные постоянные, причем постоянные и 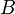не равны нулю одновременно. Вектор с координатами 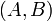называется нормальным вектором и он перпендикулярен прямой. Вектор с координатами (-B,A) или (B,-A) называется направляющим вектором.

При прямая проходит через начало координат. Также уравнение можно переписать в виде:

[править]Уравнение прямой с угловым коэффициентом

Уравнение прямой с угловым коэффициентом. Прямая линия, пересекающая ось 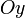в точке 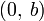и образующая угол с положительным направлением оси :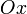

Коэффициент называется угловым коэффициентом прямой. В этом виде невозможно представить прямую, параллельную оси .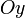

[править]Уравнение прямой в отрезках

Прямая линия, пересекающая ось 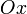в точке и ось 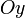в точке :

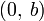В этом виде невозможно представить прямую, проходящую через начало координат.

[править]Нормальное уравнение прямой

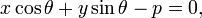
где — длина перпендикуляра, опущенного на прямую из начала координат, а — угол (измеренный в положительном направлении) между положительным направлением оси 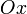и направлением этого перпендикуляра. Если , то прямая проходит через начало координат, а угол задаёт угол наклона прямой.

31. Угол между прямыми и признаки перпендикулярности и параллельности прямых на плоскости.

Угол между двумя прямыми

Рассмотрим плоскость с декартовой системой координат. И рассмотрим прямую l лежащую на этой плоскости.

Пор. Углом наклона прямой l к оси абсцисс называется угол, на который надо повернуть ось Х чтобы она стала параллельной данной прямой. Этот угол называется положительным, если поворот осуществляется против часовой стрелки.

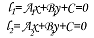
Опр. Углом наклона между прямыми l1 и l2 называется угол между направляющими векторами этих прямых.

Найдем выражение угла через cosφ.

Даны вектора m1 (-B1; A1) и m2 (-B2жA2)

Тогда угол можно найти из ab=/a/*/b/*cosφ

Пусть прямые заданы с помощью угловых коэф.

L1: y=kx+b1

L2: y=k2x+b2

tga=tg(a2-a1)=(k2-k1)/(1+k2*k1)

Угол между прямыми в пространстве.

Пусть в пространстве заданы две прямые. Их параметрические уравнения:

l₁:

l₂:

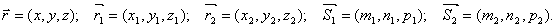
Угол между прямыми j и угол между направляющими векторами j этих прямых связаны соотношением: j = j₁ или j = 180⁰ - j₁. Угол между направляющими векторами находится из скалярного произведения. Таким образом:

.

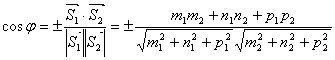Условия параллельности и перпендикулярности

прямых в пространстве.

Чтобы две прямые были параллельны необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, т.е. их соответствующие координаты были пропорциональны.

Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т.е. косинус угла между ними равен нулю.

Угол между прямой и плоскостью.

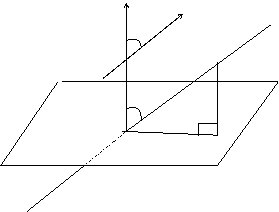
Определение. Углом между прямой и плоскостью называется любой угол между прямой и ее проекцией на эту плоскость.

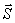
a

a

j

Пусть плоскость задана уравнением 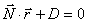, а прямая - 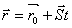. Из геометрических соображений (см. рис.) видно, что искомый угол a = 90⁰ - j, где a - угол между векторами и 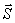. Этот угол может быть найден по формуле:

В координатной форме: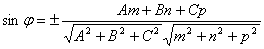

Перпендикуля́рность — бинарное отношение между различными объектами (векторами, прямыми, подпространствами и т. д.) в евклидовом пространстве. Частный случайортогональности.

Содержание [убрать] · 1 На плоскости o 1.1 Перпендикулярные прямые o 1.2 Координаты точки основания перпендикуляра к прямой o 1.3 Построение перпендикуляра · 2 В трёхмерном пространстве o 2.1 Перпендикулярные прямые o 2.2 Перпендикулярность прямой и плоскости o 2.3 Перпендикулярные плоскости · 3 В многомерных пространствах o 3.1 Перпендикулярность плоскостей в 4-мерном пространстве o 3.2 Перпендикулярность прямой и гиперплоскости o 3.3 Перпендикулярные гиперплоскости · 4 См. также

[править]На плоскости

[править]Перпендикулярные прямые

Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла.

В аналитическом выражении прямые, заданные линейными функциями и будут перпендикулярны, если выполнено условие . Эти же прямые будут перпендикулярны, если 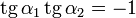. (Здесь 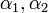— углы наклона прямой к горизонтали)

Для обозначения перпендикулярности имеется общепринятый символ: , предложенный в 1634 году французским математиком Пьером Эригоном.

[править]Координаты точки основания перпендикуляра к прямой

A(xa,ya) и B(xb,yb) - прямая, O(xo,yo) - основание перпендикуляра, опущенного из точки P(xp,yp).

xo:=(xa*(yb-ya)^2 + xp*(xb-xa)^2 + (xb-xa) * (yb-ya) * (yp-ya)) / ((yb-ya)^2+(xb-xa)^2);

yo:=(yb-ya)*(xo-xa)/(xb-xa)+ya;

[править]Построение перпендикуляра

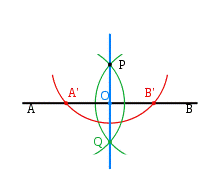
Построение перпендикуляра

Шаг 1: (красный) С помощью циркуля проведём полуокружность с центром в точке P, получив точки А' и В'.

Шаг 2: (зелёный) Не меняя радиуса, построим две полуокружности с центром в точках A' и В' соответственно, проходящими через точку Р. Кроме точки Р есть ещё одна точка пересечения этих полуокружностей, назовём её Q.

Шаг 3: (синий) Соединяем точки Р и Q. PQ и есть перпендикуляр к прямой АВ.

[править]В трёхмерном пространстве

[править]Перпендикулярные прямые

Две прямые в пространстве перпендикулярны друг другу, если они соответственно параллельны некоторым двум другим прямым, лежащим в одной плоскости и перпендикулярным в ней.

[править]Перпендикулярность прямой и плоскости

Определение: Прямая называется перпендикулярной плоскости, если она перпендикулярна всем прямым лежащим в этой плоскости.

Признак: Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости.

Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

[править]Перпендикулярные плоскости

Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90 градусам.

§ Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

§ Если из точки, принадлежащей одной из двух перпендикулярных плоскостей, провести перпендикуляр к другой плоскости, то этот перпендикуляр полностью лежит в первой плоскости.

§ Если в одной из двух перпендикулярных плоскостей провести перпендикуляр к их линии пересечения, то этот перпендикуляр будет перпендикулярен второй плоскости.

[править]В многомерных пространствах

[править]Перпендикулярность плоскостей в 4-мерном пространстве

Перпендикулярность плоскостей в четырёхмерном пространстве имеет два смысла: плоскости могут быть перпендикулярны в 3-мерном смысле, если они пересекаются по прямой (а следовательно, лежат в одной гиперплоскости), и двугранный угол между ними равен 90°.

Плоскости могут быть также перпендикулярны в 4-мерном смысле, если они пересекаются в точке (а следовательно, не лежат в одной гиперплоскости), и любые 2 прямые, проведённые в этих плоскостях через точку их пересечения (каждая прямая в своей плоскости), перпендикулярны.

В 4-мерном пространстве через данную точку можно провести ровно 2 взаимно перпендикулярные плоскости в 4-мерном смысле (поэтому 4-мерное евклидово пространство можно представить как декартово произведение двух плоскостей). Если же объединить оба вида перпендикулярности, то через данную точку можно провести 6 взаимно перпендикулярных плоскостей (перпендикулярных в любом из двух вышеупомянутых значений).

Существование шести взаимно перпендикулярных плоскостей можно пояснить таким примером. Пусть дана система декартовых координат x y z t. Для каждой пары координатных прямых существует плоскость, включающая эти две прямые. Таких пар 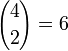: xy, xz, xt, yz, yt, zt, и им соответствуют 6 плоскостей. Те из этих плоскостей, которые включают одноимённую ось, перпендикулярны в 3-мерном смысле и пересекаются по прямой (например, xy и xz, yz и zt), а те, которые не включают одноимённых осей, перпендикулярны в 4-мерном смысле и пересекаются в точке (например, xy и zt, yz и xt).

[править]Перпендикулярность прямой и гиперплоскости

Пусть задано n-мерное евклидово пространство (n>2) и ассоциированное с ним векторное пространство , а прямая l с направляющим векторным пространством игиперплоскость с направляющим векторным пространством (где 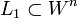, 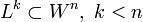) принадлежат пространству .

Прямая l называется перпендикулярной гиперплоскости , если подпространство 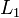ортогонально подпространству , то есть

32. Расстояние от точки до прямой.

Дата добавления: 2015-04-23