Угол между плоскостями

Пусть плоскост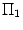и и 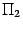заданы соответственно уравнениям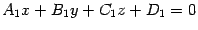и и 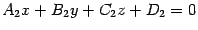. Требуется найти угол 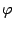между этими плоскостями.

Плоскости, пересекаясь, образуют четыре двугранных угла (рис. 11.6): два тупых и два острых или четыре прямых, причем оба тупых угла равны между собой, и оба острых тоже равны между собой. Мы всегда будем искать острый угол. Для определения его величины возьмем точку 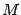на линии пересечения плоскостей и в этой точке в каждой из плоскостей проведем перпендикуляры 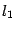и 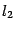к линии пересечения. 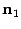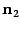Нарисуем также нормальные векторы и плоскосте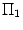й и 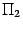с началами в точке 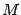(рис. 11.6).

Рис.11.6.Угол между плоскостями

Если через точку 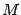провести плоскость 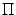, перпендикулярную линии пересечения плоскосте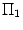й и 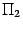, то прямые 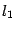и 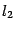и изображения векторов 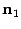и 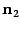будут лежать в этой плоскости. Сделаем чертеж в плоскости 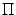(возможны два варианта: рис. 11.7 и 11.8).

Рис.11.7.Угол между нормальными векторами острый

Рис.11.8.Угол между нормальными векторами тупой

В одном варианте (рис. 11.7) 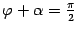и 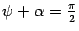, следовательно, угол между нормальными векторами равен углу 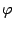, являющемуся линейным углом острого двугранного угла между плоскостям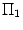и и .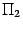

Во втором варианте (рис. 11.8) 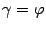, а угол между нормальными векторами равен 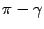. Так как

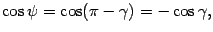
то в обоих случаях .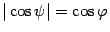

По определению скалярного произведения 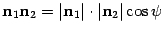. Откуда

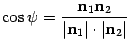
и соответственно

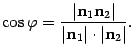
(11.4)

Так как координаты нормальных векторов известны, если заданы уравнения плоскостей, то полученная формула (11.4) позволяет найти косинус острого угла между плоскостями.

Если плоскости перпендикулярны, то перпендикулярны и их нормальные векторы. Получаем условие перпендикулярности плоскостей:

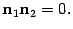
(11.5)

Если плоскости параллельны, то коллинеарны их нормальные векторы. Получаем условие параллельности плоскостей

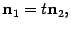
(11.6)

где 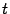-- любое число.

34. Канонические и параметрические уравнения прямой в пространстве.

§ 1. Каноническое уравнение плоскости в пространстве

Пусть в декартовой системе координат дан вектор n ={A,B,C} и точка М₀=(x₀, y₀, z₀).

Построим плоскость Π, проходящую через т. М₀, перпендикулярную вектору n (этот вектор называют нормальным вектором или нормалью плоскости).

Утверждение 1: М 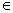Π ó М₀М 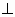n.

М₀М={ x-x₀, y-y₀, z-z₀ } 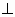n ó A(x-x₀)+B(y-y₀)+C(z-z₀)=0. (*)

(См. свойства скалярного произведения)

· Каноническое уравнение плоскости в пространстве:

Аx+By+Cz+D=0, где D = -A x₀ -B y₀ -C z₀.

Замечание 1: формула (*) используется при непосредственном решении задач, после упрощения получается искомое каноническое уравнение плоскости.

Пример 1. Написать каноническое уравнение плоскости, перпендикулярной вектору n={3,1,1} и проходящей через точку М(2,-1,1).

Пример 2. Написать каноническое уравнение плоскости, содержащей точки K(2,1,-2), L(0,0,-1), M(1,8,1).

§ 2. Канонические и параметрические уравнения прямой в пространстве

Пусть в декартовой системе координат дан вектор a ={p,q,r} и точка М₀=(x₀, y₀, z₀).

Построим прямую l, проходящую через т. М₀, параллельную вектору a (этот вектор называют направляющим вектором прямой).

Утверждение 2: М 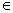l ó М₀М || a.

М₀М={ x-x₀, y-y₀, z-z₀ } || a ó 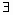t 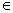R, т.ч. М₀М=t ·a =>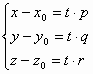

· Параметрические уравнения прямой в пространстве:

(**)

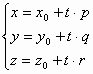Вы никогда не сталкивались с параметрическим заданием кривых? Поясним на примере: представьте себе, что по заранее намеченному маршруту с известной скоростью движется турист (автомобиль, самолёт, подводная лодка, как Вам больше понравится). Тогда, зная точку начала его путешествия, мы в любой момент времени знаем, где он находится. Таким образом, его положение на маршруте определяется всего одним параметром – временем.

В нашем случае турист движется по бесконечной прямой в пространстве, в момент времени t₀=0 он находится в точке М₀, в любой другой момент времени t его координаты в пространстве вычисляются по формулам (**).

Теперь несколько преобразуем формулы (**).

Выразим из каждой строчки параметр t: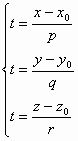

· Канонические уравнения прямой в пространстве:

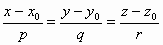
Замечание 2: Эта компактная запись на самом деле содержит три уравнения.

Замечание 3: Это формальная запись и выражение вида 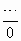в данном случае допустимо.

Замечание 4: Надо понимать, что для уравнения плоскости (прямой) играет роль именно направление перпендикулярного (направляющего) вектора, а не он сам. Т.о. вполне допустимо из каких-либо соображений заменять данный (или полученный в ходе решения) вектор на пропорциональный ему. Целесообразно также упрощать полученное уравнение, деля все его коэффициенты на общий множитель.

Пример 3. Написать канонические и параметрические уравнения прямой, параллельной заданной прямой и проходящей через заданную точку.

Пример 4. Написать канонические уравнения прямой, заданной пересечением двух плоскостей.

Пример 5. Найти точку пересечения прямой и плоскости.

§3. Расстояние от точки до плоскости в пространстве

Пусть в декартовых координатах плоскость Π задана уравнением: Ax+By+Cz+D=0, а точка М₁=(x₁,y₁,z₁).

Утверждение 3: расстояние от точки М₁ до плоскости Π вычисляется по формуле:

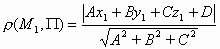
Пример 6. Найти расстояние от точки до плоскости.

§4. Координаты точки, делящей отрезок в заданном соотношении

Пусть в декартовой системе координат М₁=(x₁,y₁,z₁), М₂=(x₂,y₂,z₂).

Утверждение 4: Координаты т. М, т.ч. М₁М=λ∙ММ₂, находятся по следующим формулам:

.

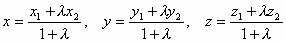35. Угол между прямой и плоскостью. Угол между прямыми.

Дата добавления: 2015-04-23