Каноническое уравнение состояния

Каноническое уравнение представляет собой выражение для одного из термодинамических потенциалов (внутренней энергии, энтальпии,свободной энергии или потенциала Гиббса) через независимые переменные, относительно которых записывается его полный дифференциал.

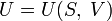§ (для внутренней энергии),

§ (для энтальпии),

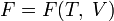§ (для энергии Гельмгольца),

§ (для потенциала Гиббса).

Каноническое уравнение, независимо от того, в каком из этих четырех видов оно представлено, содержит полную информацию о термических и калорических свойствах термодинамической системы (предполагается, что известно и определение термодинамического потенциала, такое, как F = U − TS).

38. Гипербола, ее канонические уравнения и основные характеристики

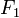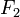Гипе́рбола (др.-греч. ὑπερβολή, от др.-греч. βαλειν — «бросать», ὑπερ — «сверх») — геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек и (называемых фокусами) постоянно. Точнее,

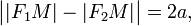причем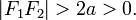

Наряду с эллипсом и параболой, гипербола является коническим сечением и квадрикой. Гипербола может быть определена как коническое сечение с эксцентриситетом, большим единицы.

Содержание [убрать] · 1 История · 2 Определения o 2.1 Коническое сечение o 2.2 Как геометрическое место точек § 2.2.1 Через фокусы § 2.2.2 Через директрису и фокус · 3 Связанные определения o 3.1 Соотношения · 4 Типы гипербол o 4.1 Гиперболы, связанные с треугольником · 5 Уравнения o 5.1 Декартовы координаты § 5.1.1 Канонический вид o 5.2 Полярные координаты · 6 Свойства o 6.1 Асимптоты o 6.2 Диаметры и хорды · 7 Касательная и нормаль · 8 Кривизна и эволюта · 9 Применения · 10 См. также · 11 Литература · 12 Примечания

[править]История

Термин «гипербола» (греч. ὑπερβολή — избыток) был введён Аполлонием Пергским (ок. 262 год до н. э. — ок. 190 год до н. э.), поскольку задача о построении точки гиперболы сводится к задаче о приложении с избытком.

[править]Определения

Гипербола может быть определена несколькими путями.

[править]Коническое сечение

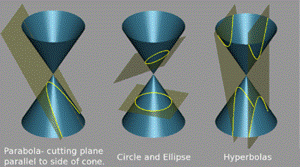
Три основных конических сечения

Гипербола может быть определена, как множество точек, образуемое в результате сечения кругового конуса плоскостью, отсекающей обе части конуса. Другими результатами сечения конуса плоскостью являются парабола, эллипс, а также такие вырожденные случаи, как скрещенные и совпадающие прямые и точка, возникающие, когда секущая плоскость проходит через вершину конуса. В частности, скрещенные прямые можно считать вырожденной гиперболой, совпадающей со своими асимптотами.

[править]Как геометрическое место точек

[править]Через фокусы

Гипербола может быть определена, как Геометрическое место точек, абсолютная величина разности расстояний от которых до двух заданных точек, называемых фокусами, постоянна.

[править]Через директрису и фокус

Геометрическое место точек, для которых отношение расстояния до фокуса и до заданной прямой, называемойдиректрисой, постоянно и больше единицы, называется гиперболой. Заданная постоянная называетсяэксцентриситетом гиперболы.

[править]Связанные определения

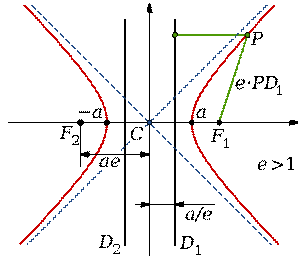
Асимптоты гиперболы (красные кривые), показанные голубым пунктиром, пересекаются в центре гиперболы, C. Два фокуса гиперболы обозначены как F ₁ и F ₂.Директрисы гиперболы обозначены линиями двойной толщины и обозначены D ₁ и D ₂. Эксцентриситет ε равен отношению расстояний точки P на гиперболе до фокуса и до соответствующей директрисы (показаны зеленым). Вершины гиперболы обозначены как ± a. Параметры гиперболы обозначают следующее:

a — расстояние от центра C до каждой из вершин
b — длина перпендикуляра, опущенного из каждой из вершин на ассимптоты
c — расстояние от центра C до любого из фокусов, F ₁ и F ₂,
θ — угол, образованный каждой из асимптот и осью, проведённой между вершинами.

§ Гипербола состоит из двух отдельных кривых, которые называют ветвями.

§ Ближайшие друг к другу точки двух ветвей гиперболы называются вершинами.

§ Кратчайшее расстояние между двумя ветвями гиперболы называется большой осью гиперболы.

§ Середина большой оси называется центром гиперболы.

§ Расстояние от центра гиперболы до одной из вершин называется большой полуосью гиперболы.

§ Обычно обозначается a.

§ Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием.

§ Обычно обозначается c.

§ Оба фокуса гиперболы лежат на продолжении большой оси на одинаковом расстоянии от центра гиперболы. Прямая, содержащая большую ось гиперболы, называется действительной или поперечной осью гиперболы.

§ Прямая, перпендикулярная действительной оси и проходящая через её центр называется мнимой или сопряженной осью гиперболы.

§ Отрезок между фокусом гиперболы и гиперболой, перпендикулярный её действительной оси, называется фокальным параметром.

§ Расстояние от фокуса до асимптоты гиперболы называется прицельным параметром.

§ Обычно обозначается b.

§ В задачах, связанных с движением тел по гиперболическим траекториям расстояние от фокуса до ближайшей вершины гиперболы называется перицентрическим расстоянием

§ Обычно обозначается ..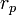

[править]Соотношения

Для характеристик гиперболы определённых выше подчиняются следующим соотношениям

§ .

§ .

§ .

§ .

§ .

§ .

§ .

§ .

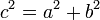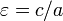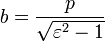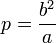[править]Типы гипербол

Равнобочная гипербола

Гиперболу, у которой , называют равнобочной. Равнобочная гипербола в некоторой прямоугольной системе координат описывается уравнением

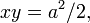
при этом фокусы гиперболы располагаются в точках (a, a) и (−a,−a).

[править]Гиперболы, связанные с треугольником

§ гипербола Енжабека — кривая, изогонально сопряженная прямой Эйлера;

§ гипербола Киперта — кривая, изогонально сопряженная прямой проходящей через точка Лемуана и центр описанной окружности данного треугольника.

См. также Треугольник#Эллипсы, параболы и гиперболы

[править]Уравнения

[править]Декартовы координаты

Гипербола задаётся уравнением второй степени в декартовых координатах (x, y) на плоскости:

,

где коэффициенты A_xx, A_xy, A_yy, B_x, B_y, и C удовлетворяют следующему соотношению

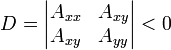
и

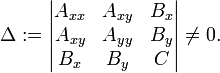
[править]Канонический вид

Перемещением центра гиперболы в начало координат и вращением её относительно центра уравнение гиперболы можно привести к каноническому виду

,

где большая a и малая b полуоси.

[править]Полярные координаты

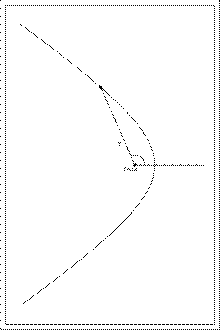
Если полюс находится в фокусе гиперболы, а вершина гиперболы лежит на продолжении полярной оси, то

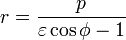
Если полюс находится в фокусе гиперболы, а полярная ось параллельна одной из асимптот, то

[править]Свойства

§ Оптическое свойство. Свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.

§ Иначе говоря, есл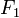и и 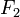фокусы гиперболы, то касательная в любой точки гиперболы является биссектрисой угла .

§ Для любой точки лежащей на гиперболе отношение расстояний от этой точки до фокуса к расстоянию от этой же точки до директрисы есть величина постоянная.

§ Гипербола обладает зеркальной симметрией относительно действительной и мнимой осей, а также вращательной симметрией при повороте на угол 180° вокруг центра гиперболы.

§ Каждая гипербола имеет сопряженную гиперболу, для которой действительная и мнимая оси меняются местами, но асимптоты остаются прежними. Это соответствует замене a и b друг на друга в формуле, описывающей гиперболу. Сопряженная гипербола не является результатом поворота начальной гиперболы на угол 90°; обе гиперболы различаются формой.

[править]Асимптоты

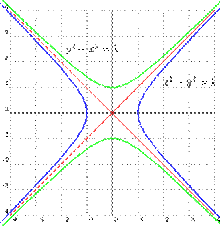
Две сопряженные гиперболы (голубая и зеленая) обладают совпадающими асимптотами (красные). Эти гиперболы единичные и равнобочные, так как a = b = 1.

Гипербола, в её каноническом виде, задается парой функций:

имеет две асимптоты

.

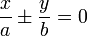[править]Диаметры и хорды

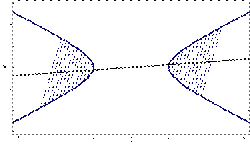
Диаметры гиперболы

Диаметром гиперболы, как и всякого конического сечения, является прямая, проходящая через середины параллельных хорд. Каждому направлению параллельных хорд соответствует свой сопряженный диаметр. Все диаметры гиперболы проходят через её центр. Диаметр, соответствующий хордам, параллельным мнимой оси, есть действительная ось; диаметр соответствующий хордам, параллельным действительной оси, есть мнимая ось.

Угловой коэффициент параллельных хорд и угловой коэффициент соответствующего диаметра связан соотношением

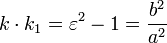
Если диаметр a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряженными. Главными диаметрами называются взаимно сопряженные и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.

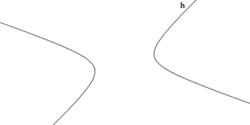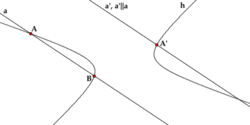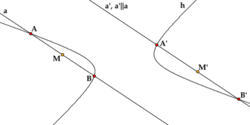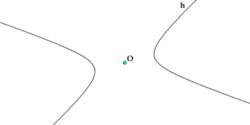
[править]Касательная и нормаль

Поскольку гипербола является гладкой кривой, в каждой её точке (x₀, y₀) можно провести касательную и нормаль. Уравнение касательной к гиперболе, заданной каноническим уравнением, имеет вид:

,

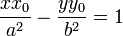или, что то же самое,

.

[показать]Вывод уравнения касательной

Уравнение нормали к гиперболе имеет вид:

.

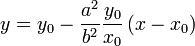[показать]Вывод уравнения нормали

[править]Кривизна и эволюта

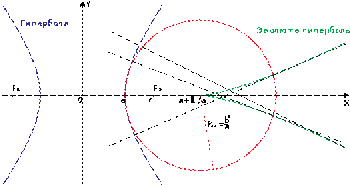
Синим цветом показана гипербола. Зеленым цветом — эволюта правой ветви этой гиперболы (эволюта левой ветви вне рисунка. Красным цветом показан круг, соответствующий кривизне гиперболы в ей вершине.)

Кривизна гиперболы в каждой её точке (x, y) определяется из выражения:

.

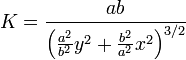Соответственно, радиус кривизны имеет вид:

.

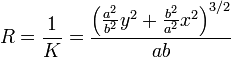В частности, в точке (a, 0) радиус кривизны равен

.

[показать]Вывод формулы для радиуса кривизны

Координаты центров кривизны задаются парой уравнений:

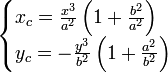
Подставив в последнюю систему уравнений вместо x и y их значения из параметрического представления гиперболы, получим пару уравнений, задающих новую кривую, состоящую из центров кривизны гиперболы. Эта кривая называется эволютой гиперболы.

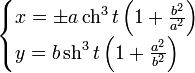
39. Парабола, ее канонические уравнения и основные характеристики.

Пара́бола (греч. παραβολή — приложение) — геометрическое место точек, равноудалённых от данной прямой(называемой директрисой параболы) и данной точки (называемой фокусом параболы).

Наряду с эллипсом и гиперболой, парабола является коническим сечением. Она может быть определена как коническое сечение с единичным эксцентриситетом.

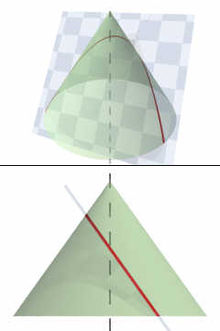
Парабола — коническое сечение

Содержание [убрать] · 1 Уравнения o 1.1 Расчёт коэффициентов квадратного уравнения · 2 Свойства · 3 Параболы в физическом пространстве · 4 См. также · 5 Ссылки · 6 Литература

[править]Уравнения

Каноническое уравнение параболы в прямоугольной системе координат:

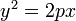(или 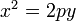, если поменять местами оси).

[показать]Вывод

Квадратное уравнение при также представляет собой параболу и графически изображается той же параболой, что и 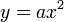, но в отличие от последней имеет вершину не в начале координат, а в некоторой точке , координаты которой вычисляются по формулам:

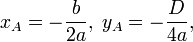где — дискриминант

Уравнение может быть представлено в виде , а в случае переноса начала координат в точку каноническим уравнением. Таким образом для каждого квадратного уравнения можно найти систему координат такую, что в этой системе оно представляется каноническим.

[править]Расчёт коэффициентов квадратного уравнения

Если для уравнения известны координаты 3-х различных точек его графика , , 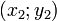, то его коэффициенты могут быть найдены так:

[править]Свойства

§ Парабола — кривая второго порядка.

§ Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и перпендикулярна директрисе.

§ Оптическое свойство. Пучок лучей, параллельных оси параболы, отражаясь в параболе, собирается в её фокусе. И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей.

§ Для параболы 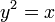фокус находится в точке (0,25; 0).

Для параболы 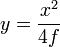фокус находится в точке (0; f).

§ Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе.

§ Парабола является антиподерой прямой.

§ Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.

§ При вращении параболы вокруг оси симметрии получается эллиптический параболоид.

Расстояние от Pn до фокуса F такое же, как и от Pn до Qn (на директрисе L)

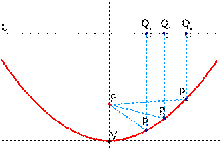
Длина линий F-Pn-Qn одинакова. Можно сказать, что, в отличие от эллипса, второй фокус у параболы — в бесконечности (см. также Шары Данделена)

Иллюстрация к доказательству теоремы Паскалячерез теорему о 9 точках

[править]Параболы в физическом пространстве

Параболический компас Леонардо да Винчи

Траектории некоторых космических тел (комет, астероидов и других), проходящих вблизи звезды или другого массивного объекта (звезды или планеты) на достаточно большой скорости имеют форму параболы (или гиперболы). Эти тела вследствие своей большой скорости не захватываются гравитационным полем звезды и продолжают свободный полёт. Это явление используется длягравитационных манёвров космических кораблей (в частности аппаратов Вояджер).

При отсутствии сопротивления воздуха траектория полёта тела в приближении однородного гравитационного поля представляет собой параболу.

Также параболические зеркала используются в любительских переносных телескопах систем Кассергена, Шмидта — Кассергена, Ньютона, а в фокусе параболы устанавливают вспомогательные зеркала, подающие изображение на окуляр.

При вращении сосуда с жидкостью вокруг вертикальной оси поверхность жидкости в сосуде и вертикальная плоскость пересекаются по параболе.

Свойство параболы фокусировать пучок лучей, параллельных оси параболы, используется в конструкциях прожекторов, фонарей, фар, а также телескопов-рефлекторов (оптических, инфракрасных, радио…), в конструкции узконаправленных (спутниковых и других) антенн, необходимых для передачи данных на большие расстояния, солнечных электростанций и в других областях.

Форма параболы иногда используется в архитектуре для строительства крыш и куполов.

40. Классификация кривых второго порядка.

Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

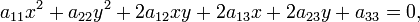
в котором по крайней мере один из коэффициентов отличен от нуля.

Дата добавления: 2015-04-23