
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Сферическая система координат в пространстве
|
|
|
|
Сферическая система координат вводится следующим образом: фиксируем плоскость, на ней -- точку О начала координат, а из точки О выпускаем луч, перпендикулярный плоскости, и луч, лежащий в плоскости. Положение точки М задаётся тремя числами: первое – расстояние от начала координат О до точки М; второе – угол между проекцией отрезка ОМ на плоскость и лежащим в плоскости лучом; третье – угол между перпендикулярным плоскости лучом и отрезком ОМ.
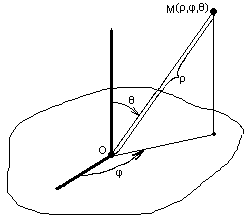
Из геометрических соображений можно получить формулы перехода между сферической и декартовой системами координат. В случае, изображённом на рисунке, формулы перехода такие:
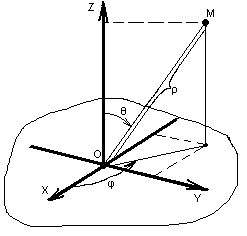
x = ρ·sinθ·cosφ,
y = ρ·sinθ·sinφ,
z = ρ·cosθ.
37. Эллипс. Каноническое уравнение. Основные характеристики эллипса.
Э́ллипс (др.-греч. ἔλλειψις — опущение, недостаток, в смысле недостатка эксцентриситета до 1) — геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных точек 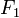 и
и 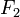 (называемыхфокусами) постоянна и больше расстояния между фокусами, то есть
(называемыхфокусами) постоянна и больше расстояния между фокусами, то есть
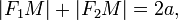 причем
причем 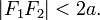
Окружность является частным случаем эллипса. Наряду с гиперболой и параболой, эллипс является коническим сечением и квадрикой. Эллипс также можно описать как пересечение плоскости и кругового цилиндра или какортогональную проекцию окружности на плоскость.
| Содержание [убрать] · 1 Связанные определения · 2 Свойства · 3 Соотношения между элементами эллипса · 4 Координатное представление o 4.1 Эллипс как кривая второго порядка o 4.2 Каноническое уравнение o 4.3 Параметрическое уравнение o 4.4 В полярных координатах · 5 Длина дуги эллипса o 5.1 Приближённые формулы для периметра · 6 Площадь эллипса и его сегмента · 7 Построение эллипса · 8 Ссылки · 9 Литература · 10 См. также |
[править]Связанные определения
§ Проходящий через фокусы эллипса отрезок AB, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2 a в вышеприведённом уравнении.
§ Отрезок CD, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса.
§ Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.
§ Точка пересечения большой и малой осей эллипса называется его центром.
§ Расстояния 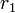 и
и 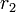 от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.
от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.
§ Расстояние 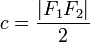 называется фокальным расстоянием.
называется фокальным расстоянием.
§ Величина 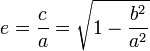 называется эксцентриситетом.
называется эксцентриситетом.
§ Диаметром эллипса называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.
§ Радиус эллипса в данной точке (расстояние от его центра до данной точки) вычисляется по формуле 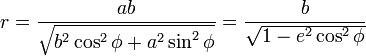 , где
, где 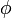 — угол между радиус-вектором данной точки и осью абсцисс.
— угол между радиус-вектором данной точки и осью абсцисс.
§ Фокальным параметром 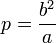 называется половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса.
называется половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса.
§ Отношение длин малой и большой полуосей называется коэффициентом сжатия эллипса или эллиптичностью: 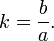 Величина, равная
Величина, равная 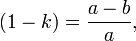 называется сжатием эллипса. Для окружности коэффициент сжатия равен единице, сжатие — нулю. Коэффициент сжатия и эксцентриситет эллипса связаны соотношением
называется сжатием эллипса. Для окружности коэффициент сжатия равен единице, сжатие — нулю. Коэффициент сжатия и эксцентриситет эллипса связаны соотношением 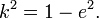
[править]Свойства
§ Оптические
§ Свет от источника, находящегося в одном из фокусов, отражается эллипсом так, что отраженные лучи пересекутся во втором фокусе.
§ Свет от источника, находящегося вне любого фокусов, отражается эллипсом так, что отраженные лучи ни в каком фокусе не пересекутся.
§ Если 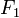 и
и 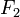 — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой
— фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой 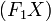 равен углу между этой касательной и прямой
равен углу между этой касательной и прямой 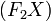 .
.
§ Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
§ Эволютой эллипса является астроида.
§ Точки пересечения эллипса с осями являются его вершинами.
§ Эксцентриситет эллипса равен отношению 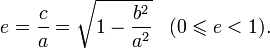 . Эксцентриситет характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
. Эксцентриситет характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
§ Эллипс также можно описать как
§ фигуру, которую можно получить из окружности, применяя аффинное преобразование
§ ортогональную проекцию окружности на плоскость.
§ Пересечение плоскости и кругового цилиндра
[править]Соотношения между элементами эллипса
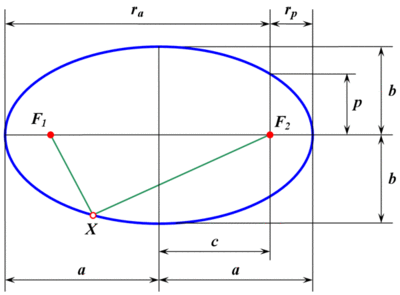

Части эллипса (описание см. в разделе "Связанные определения")
§ 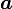 — большая полуось;
— большая полуось;
§ 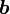 — малая полуось;
— малая полуось;
§ 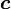 — фокальный радиус (полурасстояние между фокусами);
— фокальный радиус (полурасстояние между фокусами);
§ 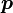 — фокальный параметр;
— фокальный параметр;
§ 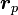 — перифокусное расстояние (минимальное расстояние от фокуса до точки на эллипсе);
— перифокусное расстояние (минимальное расстояние от фокуса до точки на эллипсе);
§ 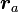 — апофокусное расстояние (максимальное расстояние от фокуса до точки на эллипсе);
— апофокусное расстояние (максимальное расстояние от фокуса до точки на эллипсе);
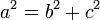
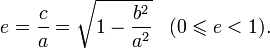 .
.
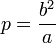
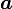
| 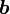
| 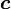
| 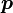
| 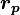
| 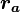
| |
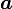 – большая полуось – большая полуось
| 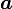
| 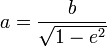
| 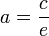
| 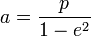
| 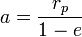
| 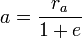
|
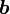 – малая полуось – малая полуось
| 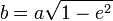
| 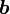
| 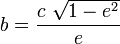
| 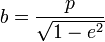
| 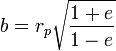
| 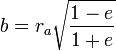
|
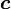 – фокальное расстояние – фокальное расстояние
| 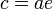
| 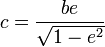
| 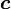
| 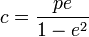
| 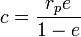
| 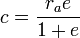
|
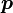 – фокальный параметр – фокальный параметр
| 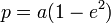
| 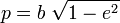
| 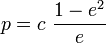
| 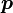
| 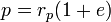
| 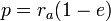
|
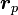 – перифокусное расстояние – перифокусное расстояние
| 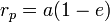
| 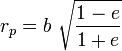
| 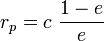
| 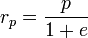
| 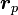
| 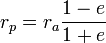
|
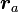 – апофокусное расстояние – апофокусное расстояние
| 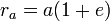
| 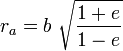
| 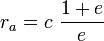
| 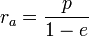
| 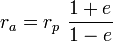
| 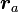
|
[править]Координатное представление
[править]Эллипс как кривая второго порядка
Эллипс является центральной невырожденной кривой второго порядка и удовлетворяет общему уравнению вида
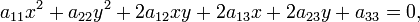
при инвариантах 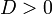 и
и 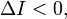 где:
где:

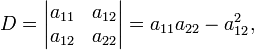
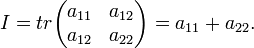
Соотношения между инвариантами кривой второго порядка и полуосями эллипса:
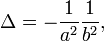
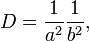
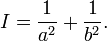
[править]Каноническое уравнение
Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса):
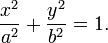
Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат.
Соотношения [показать]
[править]Параметрическое уравнение
Каноническое уравнение эллипса может быть параметризовано:
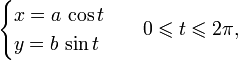
где 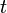 — параметр уравнения.
— параметр уравнения.
В случае окружности параметр 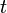 является углом между радиус-вектором данной точки и положительным направлением оси абсцисс.
является углом между радиус-вектором данной точки и положительным направлением оси абсцисс.
[править]В полярных координатах
Если принять фокус эллипса за полюс, а большую ось — за полярную ось, то его уравнение в полярных координатах 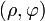 будет иметь вид
будет иметь вид
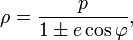
где e — эксцентриситет, а p — фокальный параметр. При положительном знаке перед e второй фокус эллипса будет находиться в точке 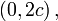 а при отрицательном — в точке
а при отрицательном — в точке 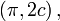 где фокальное расстояние
где фокальное расстояние 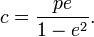
Вывод [показать]
Если принять центр эллипса за полюс, а большую ось — за полярную ось, то его уравнение в полярных координатах 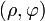 будет иметь вид
будет иметь вид
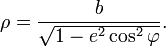
[править]Длина дуги эллипса
Длина дуги плоской линии определяется по формуле:
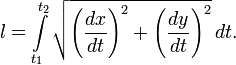
Воспользовавшись параметрическим представлением эллипса получаем следующее выражение:
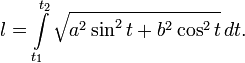
После замены 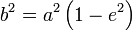 выражение для длины дуги принимает окончательный вид:
выражение для длины дуги принимает окончательный вид:
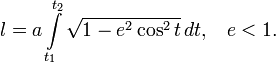
Получившийся интеграл принадлежит семейству эллиптических интегралов, которые в элементарных функциях не выражаются, и сводится к эллиптическому интегралу второго рода 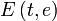 . В частности, периметр эллипса равен:
. В частности, периметр эллипса равен:
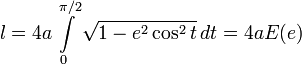 ,
,
где 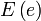 — полный эллиптический интеграл второго рода.
— полный эллиптический интеграл второго рода.
[править]Приближённые формулы для периметра
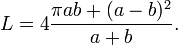
Максимальная погрешность этой формулы ~0,63 % при эксцентриситете эллипса ~0,988 (соотношение осей ~1/6,5). Погрешность всегда положительная.
Приблизительно в два раза меньшие погрешности в широком диапазоне эксцентриситетов дает формула:
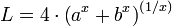 , где
, где 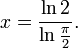
Максимальная погрешность этой формулы ~0,36 % при эксцентриситете эллипса ~0,980 (соотношение осей ~1/5). Погрешность также всегда положительная.
Cущественно лучшую точность при 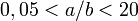 обеспечивает формула Рамануджана:
обеспечивает формула Рамануджана:
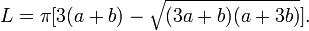
При эксцентриситете эллипса ~0,980 (соотношение осей ~1/5) погрешность составляет ~0,02 %. Погрешность всегда отрицательная.
[править]Площадь эллипса и его сегмента
Площадь эллипса вычисляется по формуле
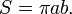
Площадь сегмента между дугой, выпуклой влево, и хордой, проходящей через точки 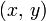 и
и 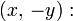
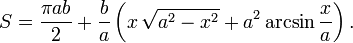
Если эллипс задан уравнением 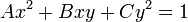 , то площадь можно определить по формуле
, то площадь можно определить по формуле
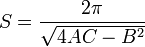 .
.
[править]Построение эллипса
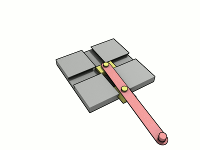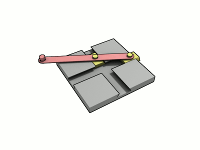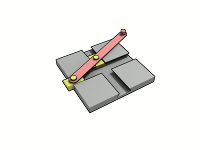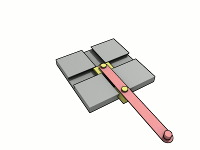

Эллипсограф в действии
Основная статья — статья «Построение эллипса» в Викиучебнике.
Инструментами для рисования эллипса являются:
§ эллипсограф;
§ две иголки, воткнутые в фокусы эллипса и соединённые ниткой длиной 2a, которую оттягивают карандашом.
При помощи циркуля или циркуля и линейки можно построить любое количество точек, принадлежащих эллипсу, но не весь эллипс целиком.
|
|
|
|
|
Дата добавления: 2015-04-23; Просмотров: 2203; Нарушение авторских прав?; Мы поможем в написании вашей работы!