Полярная система координат на плоскости

Декартова система координат на плоскости

Декартова система координат хорошо известна. И всё же сформулируем подробнее, каким образом она задаётся на плоскости, и какие величины в результате однозначно определяют положение точки на плоскости. Не будем, однако, слишком углубляться в терминологию, т.к. используемые понятия просты и подробно изучаются в курсе средней школы.

Как уже было замечено в гл.1, § 6, задать декартову систему координат на плоскости означает зафиксировать, во-первых, точку начала координат, а во-вторых, две перпендикулярные направленные оси (так называемые, оси координат). Причём, эти оси занумерованы. И, конечно, понадобится единичный отрезок, чтобы численно обозначать расстояние между двумя точками.

Таким образом, положение любой точки на плоскости однозначно определено двумя числами: первое число – величина проекции точки на первую ось (взятая с плюсом, если проекция попала на “положительную” часть оси, или с минусом, если на “отрицательную”), а второе – величина проекции на вторую ось.

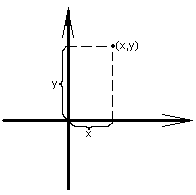
Стандартным образом декартова система координат обозначается Oxy, оси нумеруются таким образом, что поворот от первой оси ко второй осуществляется против часовой стрелки. Координаты точки – (x,y).

Для того, чтобы задать полярную систему координат на плоскости, надо зафиксировать, во-первых, точку начала координат, а во-вторых, луч, выходящий из этой точки. Необходимо также определить единичный отрезок и положительное направление отсчета угла между лучом и отрезком, соединяющим начало координат с какой-либо точкой плоскости.

Положение точки на плоскости задаётся двумя числами. Первое – расстояние от точки до начала координат, а второе – угол между зафиксированным лучом и отрезком, соединяющим точку и начало координат.

Обычно направление отсчета угла выбирают против часовой стрелки. Стандартное обозначение координат точки в полярной системе – (ρ,φ). Очевидно, ρ 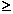0.

Существуют формулы перехода между заданными стандартным образом декартовой и полярной системами координат. Если они друг другу соответствуют (т.е. должны совпадать начала координат в обеих системах, луч полярной системы координат должен совпадать с “положительной” частью первой оси декартовой системы, должны быть одинаковыми единичные отрезки), то

x = ρ∙cosφ,

y = ρ∙sinφ.

В других случаях формулы зависят от постановки задачи, но получить их легко из геометрических соображений.

С помощью этих формул можно осуществлять переход между двумя системами координат, преобразовывать координаты точек, уравнения кривых и т.д..

В полярной системе координат очень просто выглядят уравнения прямых, проходящих через начало координат и окружностей с центром в этой точке. Кроме того, уравнения многих стандартных, часто используемых, кривых принято (с точки зрения простоты) записывать в полярных координатах.

Дата добавления: 2015-04-23