Закон сохранения момента импульса системы материальных точек

Понятие момента силы и момента импульса, связь между ними. Закон динамики вращательного движения (для материальной точки и системы материальных точек). Закон сохранения момента импульса.

Для простоты рассмотрим случай плоского движения, т.е. траектория движения материальной точки лежит в одной плоскости, которую мы расположим перпендикулярно плоскости листа. Выберем на плоскости начало координат О и положение материальной точки будем описывать радиус-вектором . Скорость точки , ее импульс , ускорение , и сила 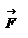будут расположены в плоски движения материальной точки, как показано на рисунке.

Введем две новые физические величины: момент силы 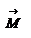и момент импульса 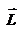относительно начала координат O. -- момент силы относительно начала координат. Модуль вектора 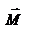равен 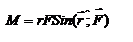, где - угол между векторами и 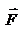. Если опустить перпендикуляр из точки O на направление действия силы, то его длина будет плечом силы , и модуль момента сил будет равен произведению силы на плечо, т.е. , что совпадает со школьным определением момента силы. Аналогично моменту силы вводится момент импульса 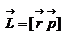- м омент импульса материальной точки относительно начала координат. 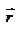, где - угол между векторами и 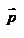, —плечо импульса , т.е. длина перпендикуляра, опущенного из точки O на направление вектора материальной точки. Оба вектора 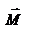и , согласно определения направлены перпендикулярно плоскости движения материальной точки. В общем случае неплоского движения, направление векторов 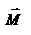и 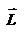не совпадают, но существует закон, который связывает момент импульса 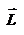с моментом силы 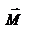. 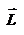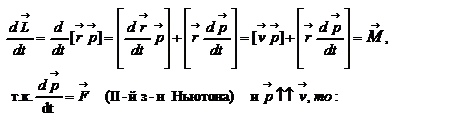Чтобы установить этот закон, возьмем производную от вектора : 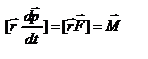.В результате получаем: -- закон изменения момента импульса материальной точки относительно начала координат.

Рассмотрим систему, состоящую из n материальных точек: Выберем начало координат О, тогда положение точек будет задаваться радиус-векторами . Пусть материальные точки обладают импульсами 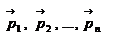, и пусть между материальными точками системы действуют силы внутреннего взаимодействия 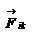, а также на материальные точки действуют внешние силы 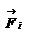. Определим моменты этих сил относительно начала координат: 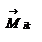- момент внутренней силы 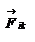, 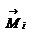- момент внешней силы 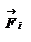. Определим также моменты импульсов материальных точек 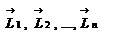. Далее для каждой материальной точки запишем закон изменения момента импульса 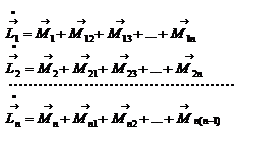Просуммировав левые и правые части этих уравнений, получим 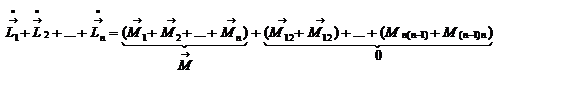Силы взаимодействия между материальными точками действуют в противоположные стороны вдоль одной и той же прямой. Их моменты относительно начала координат О равны по величине и противоположны по направлению. Поэтому моменты внутренних сил попарно уравновешивают друг друга, и сумма моментов всех внутренних сил равна нулю. В результате получим . Если система материальных точек является замкнутой, то 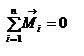, и тогда имеет место закон сохранения момента импульса 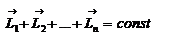- закон сохранения момента импульса системы материальных точек. Если система материальных точек является замкнутой, то суммарный момент импульса системы остаётся постоянным, т.е. сохраняется во времени.

Дата добавления: 2015-04-23