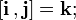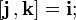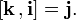КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Разложение вектора по ортам
ОРТЫ
ОПЕРАЦИИ НАД ВЕКТОРАМИ
Векторы на плоскости и в пространстве можно складывать и умножать на числа. Сложение векторов производится по правилу параллелограмма: если привести векторы к общему началу, то их суммой будет вектор, имеющий то же начало и являющийся диагональю параллелограмма, построенного на данных векторах. Произведением вектора  на число l называется вектор l
на число l называется вектор l  , коллинеарный вектору
, коллинеарный вектору  , направленный так же, как
, направленный так же, как  , если l > 0, и направленный в противоположную сторону, если l< 0, длина вектора l
, если l > 0, и направленный в противоположную сторону, если l< 0, длина вектора l  равна длине вектора
равна длине вектора  , умноженной на
, умноженной на 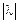 .
.
Операции над векторами удовлетворяют следующим свойствам:
 +
+ 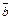 =
= 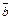 +
+ 
 + (
+ (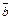 +
+ 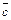 ) = (
) = ( +
+ 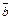 ) +
) + 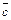
l (m  ) = (l m)
) = (l m) 
(l + m)  = l
= l  + m
+ m 
l ( +
+ 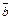 ) = l
) = l  + l
+ l 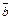
Если векторы  и
и 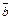 заданы своими координатами
заданы своими координатами  = (
= (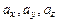 ) и
) и
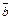 = (
= (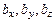 ), то
), то  +
+ 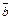 = (
= ( ), l
), l 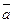 = (
= (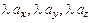 ).
).
Прямоугольная система координат(любой размерности) также описывается набором ортов, сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу. Такие орты составляют базис, притом ортонормированный.
В трёхмерном случае такие орты обычно обозначаются
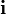 ,
, 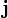 и
и 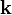
или
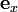 ,
, 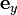 и
и 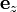 .
.
Могут также применяться обозначения со стрелками (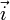 ,
, 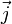 и
и 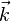 или
или 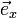 ,
, 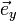 и
и 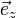 ) или другие в соответствии с обычным способом обозначения векторов в той или иной литературе.
) или другие в соответствии с обычным способом обозначения векторов в той или иной литературе.
При этом в случае правой системы координат действительны следующие формулы с векторными произведениями ортов:
Для более высоких, чем 3, размерностей (или для общего случая, когда размерность может быть любой) обычно для ортов применяют вместо этого обозначения с числовыми индексами, достаточно часто это
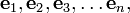
где n - размерность пространства.
Вектор любой размерности раскладывается по базису (координаты служат коэффициентами разложения):
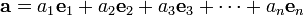
или
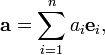
а для ортонормированного базиса координаты еще и очень легко найти через скалярные произведения с ортами:
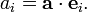
Рассмотрим векторы 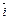 ,
,  и
и 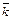 единичной длины, направленные по осям координат. Эти три вектора (на плоскости два:
единичной длины, направленные по осям координат. Эти три вектора (на плоскости два: 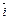 и
и 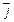 ) обладают тем свойством, что произвольный вектор
) обладают тем свойством, что произвольный вектор  может быть представлен в виде
может быть представлен в виде  =
= 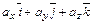 (на плоскости
(на плоскости  =
= 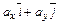 ). Эти равенства легко проверяются геометрическими построениями, поскольку на плоскости любой вектор
). Эти равенства легко проверяются геометрическими построениями, поскольку на плоскости любой вектор  является диагональю прямоугольника со сторонами, образованными векторами
является диагональю прямоугольника со сторонами, образованными векторами 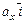 и
и 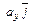 , а в пространстве — диагональю прямоугольного параллелепипеда со сторонами
, а в пространстве — диагональю прямоугольного параллелепипеда со сторонами 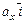 ,
, 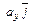 и
и 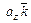 .
.
№ 2. Скалярное произведение векторов. Длина вектора. Угол между векторами. Условие ортогональности (перпендикулярности) векторов.
|
|
Дата добавления: 2015-04-24; Просмотров: 2605; Нарушение авторских прав?; Мы поможем в написании вашей работы!