Решение уравнения Шредингера для частицы в одномерной потенциальной яме

Решение уравнения Шредингера для свободной частицы.

Свободная частица это такая частица, на которую не действует никакая сила и она не находится ни в каком потенциальном поле. Поэтому она движется равномерно и прямолинейно.

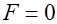и .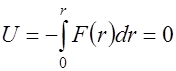

Пусть частица движется вдоль оси со скоростью .

Уравнение Шредингера имеет вид:

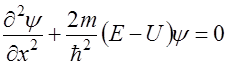
Так как , то для свободной частицы:

.

Это линейное дифференциальное уравнение второго порядка типа

,

решение которого записывается следующим образом

.

Так как:

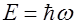и ,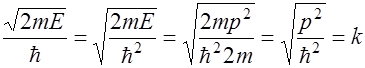

где 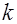- волновой вектор, то

.

Это выражение является уравнением бегущей волны, которая распространяется в двух направлениях от точки .

(рисунок)

Рассмотрим поведение частицы, которая находится в бесконечно глубокой потенциальной яме.

(рисунок)

Если - это ширина ямы, потенциальная энергия частицы задается следующим образом:

при

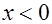
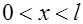
при

при .

Стационарное уравнение Шредингера имеет вид

.

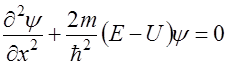Для решения уравнения зададим граничные условия в виде

,

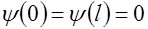так как за пределами ямы частица находится не может, поскольку ее высота равна бесконечности.

Решение этого уравнения имеет вид

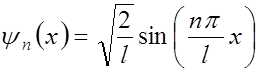, где 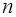- целое число, .

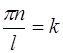Соответственно плотность вероятности нахождения частицы в каком-то месте потенциальной ямы

,

(рисунок)

Дискретным волновым числам соответствуют дискретные величины энергии частиц.

,

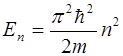так как

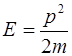и .

Величина энергии частицы, находящейся в потенциальной яме, изменяется дискретно (скачками)

(рисунок)

25. Квантовый гармонический осциллятор.

Гармоническим осциллятором называется система, которая совершает одномерное движение под действием возвращающей силы

.

Потенциальная энергия этой системы имеет вид

.

Одномерное уравнение Шредингера для гармонического осциллятора имеет вид

.

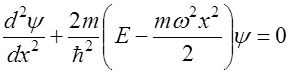Решение этого уравнения существует, если

(рисунок-график)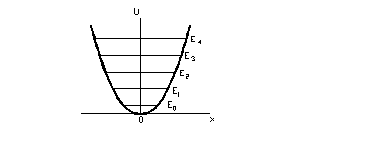

Уровни энергии у квантового гармонического осциллятора отстоят друг от друга на равные расстояния, т.е.

.

Наименьшее возможное значение энергии равно

.

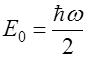Это означает, что квантовый гармонический осциллятор ни при каких условия не может иметь энергию равную нулю, что означает: и при абсолютном нуле колебания атомов в кристаллической решетке не прекращаются.

В квантовом гармоническом осцилляторе энергия изменяется скачками. При этом существует правило отбора, согласно которому энергия может изменяться только так, что уровень ее переходит только на соседний уровень:

,

т.е. энергия изменяется только порциями, равными

.

Дата добавления: 2015-04-24