Теорема. Точки М1(x1, y1) и М2(x2, y2) принадлежат разным полуплоскостям относительно прямой l тогда и только тогда, когда

ПРЯМАЯ И ПЛОСКОСТЬ. Теорема о параметрическом уравнении прямой в пространстве. Теорема об общем уравнении плоскости в пространстве. Нормальный вектор и теорема о расстоянии от точки до плоскости.

В аналитической геометрии линия на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению F(x,y)=0. При этом на функцию F должны быть наложены ограничения так, чтобы, с одной стороны, это уравнение имело бесконечное множество решений и, с другой стороны, чтобы это множество решений не заполняло “куска плоскости”. Важный класс линий составляют те, для которых функция F(x,y) есть многочлен от двух переменных, в этом случае линия, определяемая уравнением F(x,y)=0, называется алгебраической. Алгебраические линии, задаваемые уравнением первой степени, cуть прямые. Уравнение второй степени, имеющее бесконечное множество решений, определяет эллипс, гиперболу, параболу или линию, распадающуюся на две прямые.

Пусть прямая в аффинной системе координат Oxy определяется уравнением

Ax + By +C = 0. (1)

(Ax₁ + By ₁+C)(Ax₂ + By ₂+C) < 0. (2)

Доказательство. Предварительно заметим, что точка М₀(x₀, y₀) являетяс внутренней точкой отрезка [М₁М₂] тогда и только тогда, когда 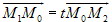, где 0 < t < 1, т.е. x₀ = x₁ + tx₂, y₀ = y₁ + ty₂, 0 < t <1. Точки М₁(x₁, y₁) и М₂(x₂, y₂) принадлежат разным полуплоскостям тогда и только тогда, когда существует точка М₀(x₀, y₀), общая для прямой l и отрезка [М₁М₂], причем точка М₀ является внутренней точкой отрезка [М₁М₂], т.е.

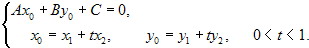
С учетом очевидного тождества С = tC + (1 - t)C получим, что точки М₁, М₂ принадлежат разным полуплоскостям тогда и только тогда, когда существует число t такое, что t(Ax₁ + By ₁+C) + (1 - t)(Ax₂ + By ₂+C) = 0, 0 < t <1, или в обозначениях Ax₁ + By ₁+C = F₁, Ax₂ + By ₂+C = F₂, (1 -t)F₁ + tF₂, 0 < t < 1. Это равносильно тому. что F₁F₂ < 0. Теорема доказана.

Итак, для координат (x, y) всех одной полуплоскости выполняется неравенство Ax + By +C > 0, а другой − неравенство Ax + By +C < 0. Полуплоскость, для точек М(x, y) которой Ax + By +C > 0, называется положительной полуплоскостью относительно уравнения (6.1.1) прямой l и обозначается символом π₊, а полуплоскость, для точек которой Ax + By +C < 0, − отрицательной полуплоскостью и обозначается π_-.

Теорема об общем уравнении плоскости в пространстве

Пусть плоскость π в аффинной системе координат Oxyz определяется уравнением

Ax + By +Cz + D = 0. (1)

Теорема 6.4. Точки М₁(x₁, y₁, z₁) и М₂(x₂, y₂, z₂) принадлежат разным полупространствам относительно плоскости π тогда и только тогда, когда

(Ax₁ + By₁+Cz₁ + D)(Ax₂ + By ₂+Cz₂ + D) < 0. (1)

Доказательство теоремы аналогично доказательству предыдущей теоремы

Полупространство, для точек М(x, y, z) которого Ax + By +Cz + D > 0, называется положительнsv полупространством относительно уравнения (1) плоскости π, а полупространство, для точек которого Ax + By +Cz + D < 0, − отрицательным полупространством.

Дата добавления: 2015-04-24