Вопрос 11

Пример

Вопрос 7.

Решение матричных уравнений.

Матричные уравнения могут иметь вид:

АХ = В, ХА = В, АХВ = С,

где А,В,С — задаваемые матрицы, Х- искомая матрица.

Чтобы решить матричное уравнение, нежно:

1.Найти обратную матрицу А^-1

2.Найти произведение обратной матрицы А^-1 на матрицу столбец свободных членов В, т.е. А^-1*В

3.Пользуясь определением равных матриц, записать ответ.

Решить уравнение АХ = В, если

Решение: Так как обратная матрица равняется (см. пример 1)

.

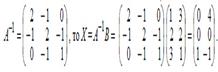
Метод Крамера.

1.Вычислить определитель матрицы, получ.из его коэффициентов.

2.Вычисслить определители Δх, Δу, Δz, получ.из матрицы А, заменой соотв. 1,2,3 столбцы столбцами свободных членов.

3.Найти значения перемены по формулам:

х= Δх/ Δ у= Δу/ Δ z= Δz/ Δ

Пример.

Система линейных уравнений:

Определители:

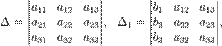
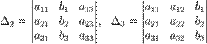
Решение:

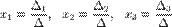
Пример:

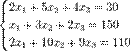
Определители:

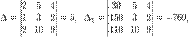
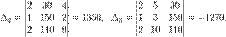
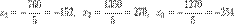
Метод Гаусса.

1.Надо составить расширенную матрицу коэффициентов матрицы А, приписав столбцы свободных членов В.

2.С помощью элементов преобразования привести матрицу к ступенчатому виду.

3.Из полученной матрицы выписать новую систему и решать ее методом исключения переменных, начиная с последнего по номеру переменных и находят все остальные.

Решить систему линейных уравнений

x₁ + 2x₂ + 5x₃ = -9,

x₁ - x₂ + 3x₃ = 2,

3x₁ - 6x₂ - x₃ = 25.

Составим расширенную матрицу коэффициентов этой системы и с помощью элементарных преобразований приведем к ступенчатому виду:

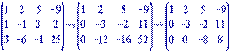
Мы приходим, следовательно, к системе уравнений

x₁ + 2x₂ + 5x₃ = -9,

-3x₂ - 2x₃ = 11,

-8x₃ = 8.

Система совместна и обладает единственным решением, т.е. определена. Находим решение полученной системы, начиная с последнего уравнения

x₁ = 2, x₂ = -3, x₃ = -1.

Исследование и решение линейных уравнений методом Жордана-Гаусса.

Метод Гаусса прекрасно подходит для решения систем линейных алгебраических уравнений (СЛАУ). Он обладает рядом преимуществ по сравнению с другими методами:

· во-первых, нет необходимости предварительно исследовать систему уравнений на совместность;

· во-вторых, методом Гаусса можно решать не только СЛАУ, в которых число уравнений совпадает с количеством неизвестных переменных и основная матрица системы невырожденная, но и системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равен нулю;

· в-третьих, метод Гаусса приводит к результату при сравнительно небольшом количестве вычислительных операций.

Опишем алгоритм метода Гаусса.

Пусть нам требуется решить систему из n линейных алгебраических уравнений с n неизвестными переменными вида 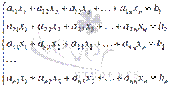, и пусть определитель ее основной матрицы отличен от нуля.

Будем считать, что 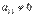, так как мы всегда можем этого добиться перестановкой местами уравнений системы. Исключим неизвестную переменную x₁ из всех уравнений системы, начиная со второго. Для этого ко второму уравнению системы прибавим первое, умноженное на 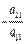, к третьему уравнению прибавим первое, умноженное на 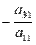, и так далее, к n-ому уравнению прибавим первое, умноженное на 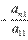. Система уравнений после таких преобразований примет вид

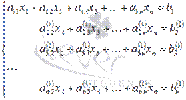
где 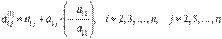, а .

К такому же результату мы бы пришли, если бы выразили x₁ через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменная x₁ исключена из всех уравнений, начиная со второго.

Далее действуем аналогично, но лишь с частью полученной системы, которая отмечена на рисунке

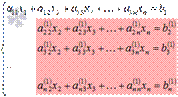
Будем считать, что (в противном случае мы переставим местами вторую строку с k-ой, где 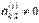). Приступаем к исключению неизвестной переменной x₂ из всех уравнений, начиная с третьего.

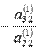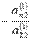Для этого к третьему уравнению системы прибавим второе, умноженное на , к четвертому уравнению прибавим второе, умноженное на , и так далее, к n-ому уравнению прибавим второе, умноженное на . Система уравнений после таких преобразований примет вид

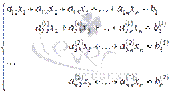
где 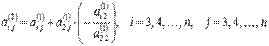, а 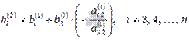. Таким образом, переменная x₂ исключена из всех уравнений, начиная с третьего.

Далее приступаем к исключению неизвестной x₃, при этом действуем аналогично с отмеченной на рисунке частью системы

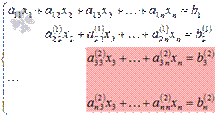
Так продолжаем прямой ход метода Гаусса пока система не примет вид

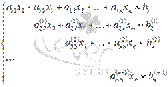
С этого момента начинаем обратный ход метода Гаусса: вычисляем x_n из последнего уравнения как 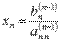, с помощью полученного значения x_n находим x_n-1 из предпоследнего уравнения, и так далее, находим x₁ из первого уравнения.

Дата добавления: 2015-04-24