Как найти направляющие косинусы вектора

Обозначьте через альфа, бета и гамма углы, образованные вектором а с положительным направлением координатных осей (см. рис.1). Косинусы этих углов называются направляющими косинусами вектора а.

Инструкция

Так как координаты а в декартовой прямоугольной системе координат равны проекциям вектора на координатные оси, то
а1 = |a|cos(альфа), a2 = |a|cos(бета), a3 = |a|cos(гамма). Отсюда:
cos (альфа)=a1||a|, cos(бета) =a2||a|, cos(гамма)= a3/|a|.
При этом |a|=sqrt(a1^2+ a2^2+ a3^2). Значит
cos (альфа)=a1|sqrt(a1^2+ a2^2+ a3^2), cos(бета) =a2|sqrt(a1^2+ a2^2+ a3^2),
cos(гамма)= a3/sqrt(a1^2+ a2^2+ a3^2).

Следует отметить основное свойство направляющих косинусов. Сумма квадратов направляющих косинусов вектора равна единице.
Действительно, cos^2(альфа)+cos^2(бета)+cos^2(гамма)=
= a1^2|(a1^2+ a2^2+ a3^2)+ a2^2|(a1^2+ a2^2+ a3^2)+ a3^2/(a1^2+ a2^2+ a3^2) =
=(a1^2+ a2^2+ a3^2)|(a1^2+ a2^2+ a3^2) = 1.

Первый способ

Пример: дано: вектор а={1, 3, 5). Найти его направляющие косинусы.
Решение. В соответствии с найденным выпишем:
|а|= sqrt(ax^2+ ay^2+ az^2)=sqrt(1+9 +25)=sqrt(35)=5,91.
Таким образом, ответ можно записать в следующей форме:
{cos(альфа), cos(бета), cos(гамма)}={1/sqrt(35), 3/sqrt (35), 5/(35)}={0,16;0,5;0,84}.

Второй способ

При нахождении направляющих косинусов вектора а, можно использовать методику определения косинусов углов с помощью скалярного произведения. В данном случае в виду имеются углы между а и направляющими единичными векторами прямоугольных декартовых координат i, j и k. Их координаты {1, 0, 0}, {0, 1, 0}, {0, 0, 1}, соответственно.
Следует напомнить, что скалярное произведение векторов определяется так.

Если угол между векторами ф, то скалярное произведение двух ветров (по определению) – это число, равное произведению модулей векторов на cosф. (a, b) = |a||b|cos ф. Тогда, если b=i, то (a, i) = |a||i|cos(альфа),
или a1 = |a|cos(альфа). Далее все действия выполняются аналогично способу 1, с учетом координат j и k.

Вопрос 6.

Векторное произведение: определение и свойства. Площадь параллелограмма и треугольника.Выражение скалярного произведения через координаты. Примеры.

В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов 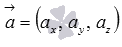и 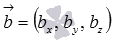есть вектор 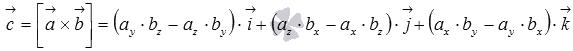, где - координатные векторы.

Это определение дает нам векторное произведение в координатной форме.

Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты , во второй строке находятся координаты вектора 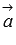, а в третьей – координаты вектора 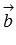в заданной прямоугольной системе координат:

Дата добавления: 2015-04-24