Геометрический смысл векторного произведения

Свойства векторного произведения.

Так как векторное произведение в координатах представимо в виде определителя матрицы 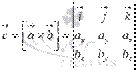, то на основании свойств определителя легко обосновываются следующие свойства векторного произведения:

1. антикоммутативность ;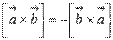

2. свойство дистрибутивност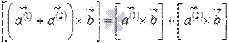и или ;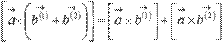

3. сочетательное свойство 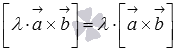или , где 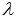- произвольное действительное число.

Для примера докажем свойство антикоммутативности векторного произведения.

По определению и 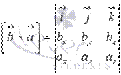. Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому, , что доказывает свойство антикоммутативности векторного произведения.

По определению длина векторного произведения векторов равна 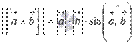. А из курса геометрии средней школы нам известно, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними. Следовательно, длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы 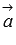и 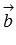, если их отложить от одной точки. Другими словами, длина векторного произведения векторов 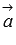и 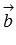равна площади параллелограмма со сторонами и 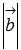и углом между ними, равным 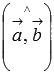. В этом состоит геометрический смысл векторного произведения.

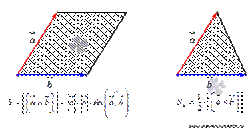
Пример.

В прямоугольной декартовой системе координат дан параллелограмм ABCD, 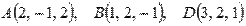. Используя векторное произведение, определите площадь треугольника АВD и площадь параллелограмма АВCD.

Решение.

Обозначим площадь треугольника АВD через 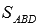, а площадь параллелограмма 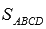. В геометрическом смысле длина векторного произведения 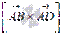равна площади параллелограмма АВCD, то есть, 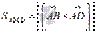, следовательно, . Итак, решение задачи свелось к нахождению длины векторного произведения.

Для этого сначала определяем координаты векторов 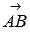и :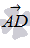

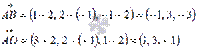
Теперь по их координатам находим векторное произведение

Вычисляем длину векторного произведения по его координатам .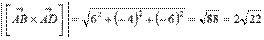

Таким образом, 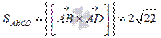и .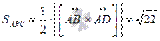

Ответ:

Выражение скалярного произведения через координаты

Представим перемножаемые векторы в разложении по базисным векторам декартовой системы координат и перемножим их, воспользовавшись свойствами векторного произведения,

Как видно, векторное произведение представляется определителем третьего порядка, в первой строчке которого проставляются базисные векторы декартовой системы координат, во второй строчке — координаты первого вектора – сомножителя, в третьей строчке — координаты второго вектора – сомножителя.
Используя свойства определителей, можно обосновать свойства векторного произведения. Так свойство

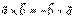
соответствует изменению знака определителя при перестановке двух его строк. Далее, если векторы коллинеарны, то их векторное произведение равно нулю, это соответствует пропорциональности второй и третьей строчек. То есть, условием коллинеарности векторов является пропорциональность их соответствующих координат.

Дата добавления: 2015-04-24