Вопрос 5. Плоскость в пространстве

Плоскость в пространстве. Нормальное уравнение плоскости. Примеры.

Плоскость в пространстве

Определение. Линейным уравнением относительно переменных x, y, z называется уравнение вида Ax + By + Cz + D = 0, где хотя бы один из коэффициентов А, В, С отличен от нуля.

Теорема. Всякая плоскость в пространстве определяется линейным уравнением

и обратно, всякое линейное уравнение (3) определяет плоскость в пространстве.

Выбираем на ней какую-либо точку M₀(x_{0, y}0, z₀), и в некоторой точке плоскости (P) построим ненулевой вектор 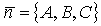, перпендикулярный плоскости (P). Для того, чтобы произвольная точка M(x, y, z) пространства принадлежала плоскости (P), необходимо и достаточно, чтобы 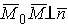, то есть

Уравнение (4) называется векторным уравнением плоскости.

Т.к. 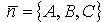и 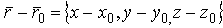, то скалярное произведение в (4) можем заменить через координаты сомножителей, а именно:

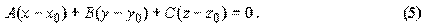
Уравнение (5) перепишем в виде:

где D = -Ax₀ - By₀ - Cz₀, то есть получим уравнение (3). Это показывает, что любая плоскость может быть описана уравнением (3).

Уравнение (3) называют общим уравнением плоскости, а уравнение (5) - уравнением плоскости, проходящей через заданную точку M0(x0, y0, z0). Отметим, что вектор 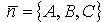называют нормальным вектором плоскости и в качестве нормального вектора плоскости может быть взят любой ненулевой вектор, перпендикулярный плоскости.

Легко доказывается и обратное: дано уравнение Ax + By + Cz + D = 0 и нужно убедиться, что оно описывает плоскость в пространстве R³.

Пусть (x0, y0, z0) - какое-либо решение данного уравнения. Тогда Ax₀ + By₀ + Cz₀ + D = 0. Отсюда получаем D = -Ax₀ - By₀ - Cz₀ и, подставляя в исходное уравнение, получаем:
Ax + By + Cz -Ax₀ - By₀ - Cz₀ = 0, или
A(x - x₀) + B(y- y₀) + C(z - z₀) = 0. а это есть уравнение плоскости, проходящей через точку (x₀, y₀, z₀) и имеющую нормальный вектор .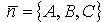

Следовательно, и равносильное ему уравнение Ax + By + Cz + D = 0 определяет плоскость. Теорема доказана.

Рассмотрим важный частный случай построения уравнения плоскости, когда известны три точки M₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂), M₃(x₃, y₃, z₃), принадлежащие плоскости и не лежащие на одной прямой. Возьмем текущую точку M(x, y, z) плоскости и организуем три вектора

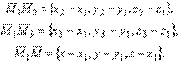
Эти векторы лежат в одной плоскости, уравнение которой и определяется. Следовательно, их смешанное произведение равно нулю, то есть

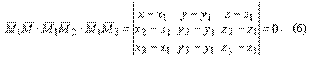
Уравнение (6) и есть уравнение плоскости, проходящей через три заданные точки M₁, M₂, M₃.

При решении задач часто используется так называемое уравнение плоскости в отрезках на осях. Пусть в общем уравнении плоскости (3) A ≠ 0, B≠ 0, C≠ 0, D≠ 0. Перенесем свободный член D в правую часть и разделим обе части уравнения на - D, тогда получим:

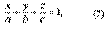
где

Уравнение (7) и называют уравнением плоскости в отрезках на осях, т.к. числа a, b, c имеют простой геометрический смысл: а - абсцисса точки пересечения плоскости с осью Ох, b - ордината точки пересечения плоскости с осью Оу, с - аппликата точки пересечения плоскости с осью Oz. Действительно, точка пересечения плоскости с осью, скажем, Ох имеет ординату у = 0 и аппликату z = 0. Но координаты этой точки (х,0,0) должны удовлетворять уравнению плоскости, т.е.

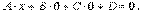
Отсюда получаем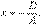

Нормальное уравнение плоскости.

Пусть дана плоскость 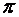. Проведем через начало координат прямую , будем называть эту прямую нормалью; точка - пересечение плоскости 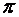и нормали 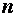. Обозначим через 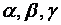углы, которые составляет вектор 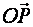с осями координат; . Выведем уравнение плоскости 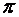, считая известными 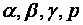. Для этого возьмем на плоскости 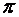произвольную точку 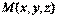, тогда 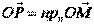, отсяда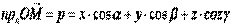

Или

(7)

(7) – нормальное уравнение плоскости

Пример.

Решим теперь задачу о вычислении угла между двумя плоскостями. Угол между двумя плоскостями, точнее, один из двух смежных углов между двумя плоскостями, может быть вычислен как угол между нормальными векторами этих плоскостей. Если плоскости заданы своими общими уравнениями

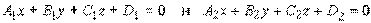
то их нормальные векторы имеют вид и потому угол Θ между плоскостями находим по формуле

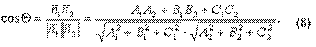
Условием параллельности двух плоскостей является условие

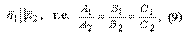
а условием перпендикулярности двух плоскостей является условие

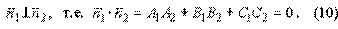
Дата добавления: 2015-04-24