Вопрос 1. Однородные системы. Фундаментальные системы решений

Вопрос 12.

Однородные системы. Фундаментальные системы решений.

Векторная алгебра.

Понятие вектора. Линейные опереции над векторами: сложение векторов и умножение на число. Линейные свойства векторов. Примеры.

Вектор-направленный отрезок

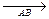, А-начало вектора

В-конец вектора

Длина вектора-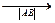

Векторы называются коллинеарными, если они расположены на одной или на параллельных прямых.

Нулевой вектор коллинеарен любому вектору.

Векторы называются компланарными, если существует плоскость, которой они параллельны. Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.

Векторы называются равными, если они коллинеарны, сонаправлены и имеют одинаковые модули.

Всякие векторы можно привести к общему началу, т. е. построить векторы, равные данным и имеющие общее начало.

Линейными операциями над векторами являются сложение и умножение на число.

Суммой векторов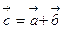

Произведением векторов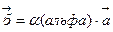

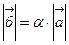
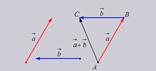Сумма векторов по правилу треугольника

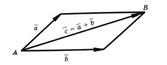По правилу параллелограмма

Свойства векторов:

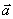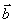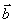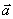+ = + - коммутативность;

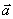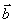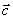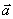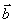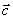+ ( + ) = ( + ) + - ассоциативность (по сложению);

+ = ;

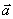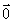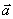1 × = ;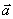

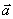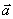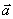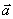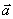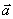+ (- ) = - = + (-1) = ;

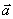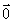α (β 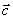) = (αβ) 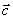- ассоциативность (по отношению к числам);

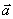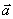(α + β) = α + β 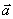- дистрибутивность (по отношению к умножению на вектор);

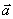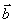α 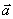( + ) = α + α 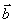- дистрибутивность (по отношению к умножению на число).

α, β - числа.

Свойства линейнонезависимых и линейнозависимых векторов:

1) Если к линейно зависимой системе векторов 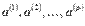добавить несколько векторов, то полученная система будет линейно зависимой.

2) Если из линейно независимой системы векторов 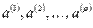исключить несколько векторов, то полученная система будет линейно независимой.

3) Если в системе векторов 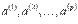есть хотя бы один нулевой вектор, то такая система линейно зависимая.

4) Если система векторов 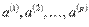линейно зависима, то хотя бы один из ее векторов линейно выражается через остальные. Если система векторов 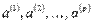линейно независима, то ни один из векторов не выражается через остальные.

Дата добавления: 2015-04-24