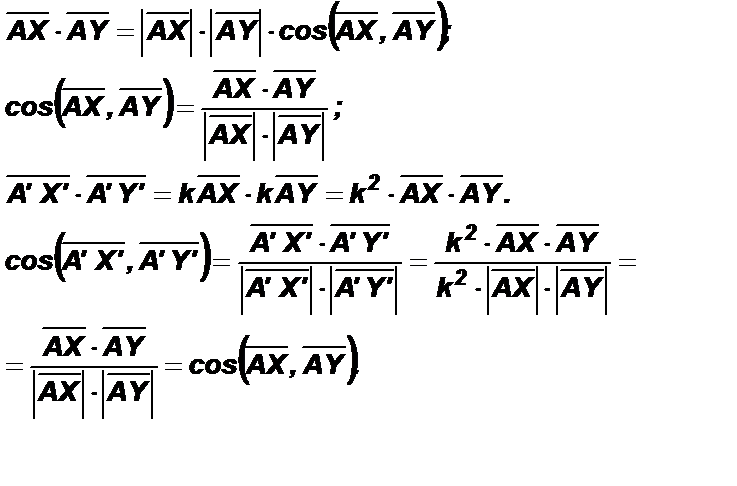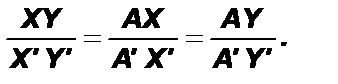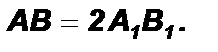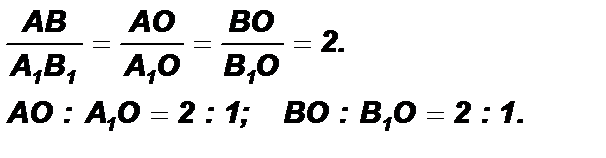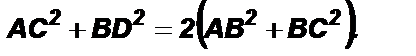Гомотетия переводит треугольник в треугольник. Стороны этих треугольников пропорциональны, а соответственные углы равны

Гомотетия сохраняет величину угла..

Докажем, что ÐXAY = ÐX’A’Y’.

По определению скалярного произведения векторов:

А’

А

Y’

Y

X

O

X’

Из равенства косинусов ÐXAY и ÐX’A’Y’ следует равенство самих углов.

А’

А

Y’

Y

X

O

X’

Докажем, что при гомотетии треугольник переходит в подобный ему треугольник, у которого: что ÐA = ÐA’; ÐY = ÐY’; ÐX = ÐX’.

По первому свойству гомотетии отрезки XY, AX, AY переходят соответственно в отрезки X’Y’, A’X’, A’Y’.

По второму свойству гомотетии углы ÐA, ÐY, ÐX переходят в углы ÐX’, ÐA’ и ÐY’ соответственно.

35. Доказать теорему о точке пересечения медиан треугольника.

Теорема о свойстве медиан треугольника. Три медианы пересекаются в одной точке. Эта точка делит каждую из медиан в отношении 2:1, считая от вершины.

С

В

В₁

А₁

А

О

Доказательство:

1). Медиана АА₁ пересекает АВ в точке А₁. Медиана ВВ₁ пересекает АС в точке В₁. Тогда А₁В₁– средняя линия.

2). Рассмотрим D АОВ и D А₁ОВ₁.

3). Из подобия треугольников:

4). Аналогично доказывается, что точка О делит медиану СС₁ в отношении 2:1.

36. Доказать теорему о сумме квадратов диагоналей параллелограмма.

Теорема. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

А

В

С

D

О

Дано:

ABCD – параллелограмм;

AC ∩ BD = {O}.

Доказать:

Доказательство:

Дата добавления: 2015-04-24