Момент импульса. Закон сохранения момента импульса

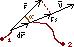
Момент импульса (количество движения) мт А относительно неподвижной точки О – физическая величина, определяемая векторным произведением:

,

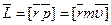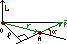
где r-радиус-вектор, проведённый из точки О в точку А; 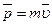- импульс мт. 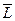-псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от 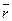к .

Модуль вектора момента импульса:

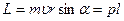
Момент импульса относительно неподвижной оси z называется скалярная величина L_z, равная проекции на эту ось вектора момента импульса, определённого относительно произвольной точки О данной оси.

Т.к. 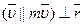, то момент импульса отдельной частицы:

.

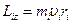Момент импульса твёрдого тела относительно оси есть сумма моментов импульса отдельных частиц, а т.к. 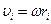, то:

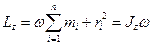, т.о. момент импульса твёрдого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость.

Продифференцируем последнее уравнение: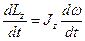

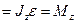
, т.е.: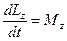

это и есть уравнение динамики вращательного движения твёрдого тела относительно неподвижной оси: Производная момента импульса твёрдого тела относительно оси равна моменту сил относительно той же оси.

Можно показать, что имеет место векторное равенство:

.

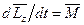В замкнутой системе момент внешних сил 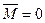и 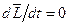, откуда: L=const, это выражение и есть закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени.

12. Работа силы. Мощность.

Энергия – универсальная мера различных форм движения и взаимодействия.

Работа силы – величина, характеризующая процесс обмена энергией между взаимодействующими телами в механике.

Если тело движется прямолинейно и на него действует постоянная сила 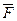, которая составляет некоторый угол 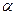с направлением перемещения, то работа этой силы равна произведению проекции силы F_s на направление перемещения, умноженной на перемещение точки приложения силы:

.

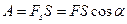Элементарная работа силы 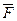на перемещении 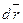называется скалярная величина, равная:

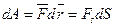, где , , .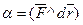

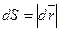Работа силы на участке траектории от 1 до 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути:

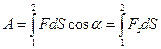
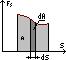, если на графике изображена зависимость F_s от S, то работа определяется на графике площадью закрашенной фигуры.

При 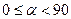, то А>0

При 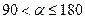, то А<0,

При 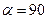, то А=0.

Мощность – скорость совершения работы.

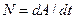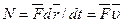, , т.е. мощность равна скалярному произведению вектору силы на вектор скорости, с которой движется точка приложения силы.

13. Кинетическая и потенциальная энергия поступательного и вращательного движения.

Кинетическая энергия механической системы – энергия механического движения этой системы. dA=dT. По 2зН 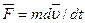, помножим на 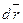и получим:

;

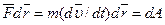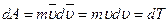, отсюда:

.

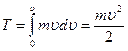Кинетическая энергия системы – есть функция состояния её движения, она всегда , и зависит от выбора системы отсчёта.

Потенциальная энергия – механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.

Если силовое поле характеризуется тем, что работа совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории, по которой это перемещение произошло, а зависит только от начального и конечного положений, то такое поле называется потенциальным, а силы, действующие в нём – консервативными, если же работа зависит от траектории то такая сила – диссипативная.

Т.к. работа совершается за счёт убыли потенциальной энергии, то: 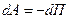; ; 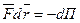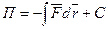, где С – постоянная интегрирования, т.е. энергия определяется с точностью до некоторой произвольной постоянной.

Если силы консервативны, то:

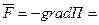
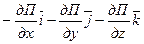- Градиент скаляра П. (также обозначается ).

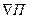При П=mgh.

Т.к. начало отсчёта выбирается произвольно, то потенциальная энергия может иметь отрицательное значение. (при П=-mgh’).

Найдём потенциальную энергию пружины.

Сила упругости: 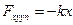, по 3зН: F_x=-F_xупр=kx;

dA=F_xdx=kxdx;

.

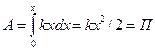Потенциальная энергия системы является функцией состояния системы, она зависит только от конфигурации системы и от её положения по отношению к внешним телам.

Полная механическая энергия системы – энергия механического движения и взаимодействия: Е=Т+П, т.е. равна сумме кинетической и потенциальной энергий.

Дата добавления: 2015-04-24