Кинетическая энергия вращения

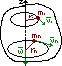
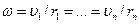
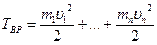
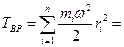
14. Механическая энергия. Закон сохранения механической энергии.

Полная механическая энергия системы – энергия механического движения и взаимодействия: Е=Т+П, т.е. равна сумме кинетической и потенциальной энергий.

Пусть F₁’…F_n’ – равнодействующие внутренних консервативных сил. F₁…F_n - равнодействующие внешних консервативных сил. f₁…f_n. Запишем уравнения 2зН для этих точек:

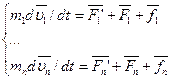
Умножим каждое ур-е на 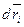, учтя, что .

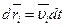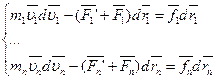
Сложим ур-я:

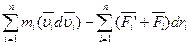
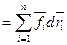
Первый член левой части:

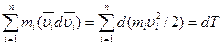
Где dT есть приращение кинетической энергии системы.

Второй член 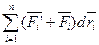равен элементарной работе внутренних и внешних сил, взятой со знаком минус, т.е. равен элементарному приращению потенциальной энергии dП системы.

Правая часть равенства задаёт работу вешних неконсервативных сил, действующих на систему. Т.о.:

.

Если внешние неконсервативные силы отсутствуют, то:

d(Т+П)=0;

Т+П=Е=const

Т.е. полная механическая энергия системы сохраняется постоянной. Закон сохранения механической энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т.е. не изменяется со временем.

15. Абсолютно упругий удар.

Удар (соударение) – столкновение 2-х или более тел, при котором взаимодействие длится очень короткое время. При ударе внешними силами можно пренебречь.

Коэффициент восстановления – отношение нормальной составляющей относительной скорости тел после и до удара.

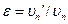, если для сталкивающих тел 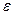=0, то такие тела называются абсолютно неупругими, если =1 то абсолютно упругими.

Линия удара – прямая проходящая через точку соприкосновения тел и нормальная к поверхности их соприкосновения.

Центральный удар – такой удар, при котором тела до удара движутся вдоль прямой, проходящей через их центр масс.

Абсолютно упругий удар – столкновение 2-х тел, в результате которого в обоих взаимодействующих не остаётся ни каких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию.

Для абсолютно упругого удара выполняются закон сохранения импульса и закон сохранения энергии.

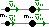
Законы сохранения:

m₁v₁+m₂v₂=m₁v’₁+m₂v’₂

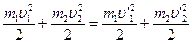
после преобразований:

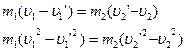
откуда:

v₁+v₁’=v₂+v₂’

решая последнее ур-е и предпедпоследнее найдём:

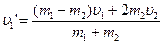
16. Абсолютно неупругий удар.

Удар (соударение) – столкновение 2-х или более тел, при котором взаимодействие длится очень короткое время. При ударе внешними силами можно пренебречь.

Коэффициент восстановления – отношение нормальной составляющей относительной скорости тел после и до удара.

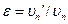, если для сталкивающих тел 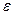=0, то такие тела называются абсолютно неупругими, если 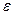=1 то абсолютно упругими.

Линия удара – прямая проходящая через точку соприкосновения тел и нормальная к поверхности их соприкосновения.

Центральный удар – такой удар, при котором тела до удара движутся вдоль прямой, проходящей через их центр масс.

Абсолютно неупругий удар – столкновении 2-х тел, в результате которого тела объединяются, двигаясь дальше, как единое целое.

Закон сохранения импульса:

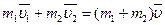
отсюда:

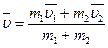
Если шары двигались навстречу друг другу, то при абсолютно неупругом ударе шары движутся в сторону большего импульса.

17. Поле тяготения, напряжённость, потенциал.

Закон всемирного тяготения: между любыми двумя мт действует сила взаимного притяжения, прямо пропорциональная произведению масс этих точек и обратно пропорциональная квадрату расстояния между ними:

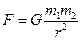
G – Гравитационная постоянная (G=6,67*10^-11 Hm²/(кг)²)

Гравитационное взаимодействие между двумя телами осуществляется с помощью поля тяготения, или гравитационного поля. Это поле порождается телами и является формой существования материи. Основное св-во поля в том, что на всякое тело внесённое в это поле действует сила тяготения:

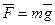
Вектор 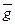не завит от массы и называется напряжённостью поля тяготения.

Напряжённость поля тяготения определяется силой действующей со стороны поля на мт единичной массы, и совпадает по направлению с действующей силой, напряжённость есть силовая хар-ка поля тяготения.

Поле тяготения однородное если напряжённость во всех точках его одинакова, и центральным, если во всех точках поля векторы напряжённости направлены вдоль прямых, которые пересекаются в одной точке.

Гравитационное поле тяготения – носитель энергии.

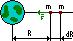
На расстоянии R на тело действует сила:

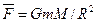
при перемещении этого тела на расстояние dR затрачивается работа:

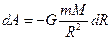
Знак минус появляется, т.к. сила и перемещение в данном случае противоположны по направлению.

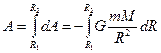
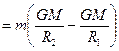
Затраченная работа в пол тяготения не зависит от траектории перемещения, т.е. илы тяготения консервативны, а поле тяготения является потенциальным.

;

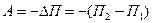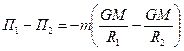
Если 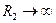то П₂=0, тогда запишем:

.

,

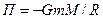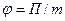Потенциал поля тяготения – скалярная величина, определяемая потенциальной энергией тела единичной массы в данной точке поля или работой по перемещению единичной массы из данной точки поля в бесконечность. Т.о.:

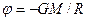
Эквипотенциальные – такие поверхности, для которых потенциал постоянен.

Взаимосвязь между потенциалом и напряженностью.

;

;

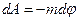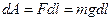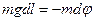
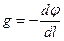
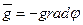
Знак мину указывает на то, что вектор напряжённости направлен в сторону убывания потенциала.

Если тело находится на высоте h, то

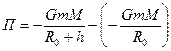
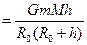
18. Неинерциальная система отсчёта. Силы инерции при ускоренном поступательном движении системы отсчёта.

Неинерциальная – система отсчёта, движущаяся относительно инерциальной системы отсчёта с ускорением.

Законы Н можно применять в неинерциальной системе отсчёта, если учесть силы инерции. Силы инерции при этом должны быть такими, чтобы вместе с силами 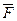, обусловленными воздействием тел друг на друга, они сообщали телу ускорение 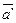, каким оно обладает в неинерциальных системах отсчёта, т.е.:

; .

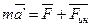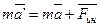Дата добавления: 2015-04-24