Силы инерции при ускоренном поступательном движении системы отсчёта

;

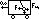
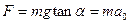, т.е. угол отклонения нити от вертикали равен:

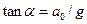
Относительно системы отсчёта, связанной с тележкой шарик покоится, что возможно, если сила F уравновешивается равной и противоположно направленной ей силой F_ин, т.е.:

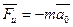
19. Силы инерции, действующие на тело, покоящееся во вращающейся системе отсчёта.

Пусть диск равномерно вращается с угловой скоростью вокруг вертикальной оси, проходящей через его центр. На диске на разных расстояниях от оси вращения установлены маятники (на нитях подвешены шарики). При вращении маятников вместе с диском шарики отклоняются от вертикали на некоторый угол.

В инерциальной системе отсчёта, связанной с помещением, на шарик действует сила, равная , и направлена перпендикулярно оси вращения диска. Она является равнодействующей силы тяжести и силы натяжения нити :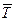

.

Когда движение шарика установится, то:

;

,

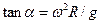т.е. углы отклонения нитей маятников будут тем больше, чем больше расстояние R от шарика до оси вращения диска и чем больше угловая скорость вращения .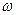

Относительно системы отсчёта, связанной с вращающимся диском, шарик покоится, что возможно, если сила 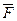уравновешивается равной и противоположно направленной ей силой .

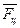Сила 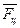, называемая центробежной силой инерции, направлена по горизонтали от оси вращения диска и равна:

.

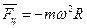20. Силы инерции, действующие на тело, движущееся во вращающейся системе отсчёта. Кориолисова сила.

Пусть шарик движется с постоянной скоростью вдоль радиуса равномерно вращающегося диска .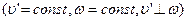

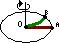
Если диск не вращается, то шарик, двигаясь по радиальной прямой, попадает в точку А, если же диск привести во вращение, то шарик катится по кривой ОВ, причём его скорость относительно диска изменяет своё направление. Значит, на шарик действует сила, перпендикулярная скорости.

Для того, чтобы заставить шарик катится вдоль радиуса, используем жёстко укреплённый вдоль радиуса стержень, на котором шарик движется равномерно и прямолинейно со скоростью . При отклонении шарика стержень действует на него некоторой силой 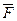. Относительно системы отсчёта, связанной с диском шарик движется равномерно и прямолинейно, т.к. сила 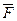уравновешивается силой 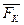. Эта сила называется кориолисовой силой инерции.

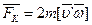
Вектор 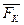перпендикулярен векторам скорости и угловой скорости вращения системы отсчёта, в соответствии с правилом правого винта.

21. Гидростатическое давление, закон Архимеда, закон неразрывности струи.

Гидроаэромеханика – раздел механики, изучающий равновесие и движение жидкостей и газов, их взаимодействие между собой и обтекаемыми ими твёрдыми телами.

Несжимаемая жидкость – жидкость, плотность которой всюду одинакова и не изменяется со временем.

Давление – физическая величина, определяемая нормальной силой, действующей о стороны жидкости на единицу площади:

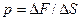
Закон Паскаля – давление в любом месте покоящейся жидкости одинаково по всем направлениям, причём давление одинаково передаётся по всему объёму, занятому покоящейся жидкости.

Если жидкость не сжимаема, то при поперечном сечении S столба жидкости, его высоте h и плотности вес:

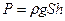
А давление на нижнее основание:

,

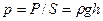т.е. давление изменяется линейно с высотой. Давление называется гидростатическим давлением.

Из этого следует, что давление на нижние слои жидкости будет больше, чем на верхние, значит на тело, погружённое в жидкость действует выталкивающая сила, определяемая законом Архимеда: на тело погружённое в жидкость (газ), действует со стороны этой жидкости направленная вверх выталкивающая сила, равная весу вытесненной телом жидкости:

,

Течение – движение жидкости.

Поток – совокупность частиц движущейся жидкости.

Линии тока – графическое изображение движения жидкости.

Течение жидкости установившееся (стационарно), если форма расположения линий тока, а так же значения скоростей в каждой её точке со временем не изменяются.

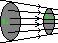
За 1с через сечение S₁ пройдёт объём жидкости равный , а через S₂ - , здесь предполагается, что скорость жидкости в сечении постоянна. Если жидкость не сжимаема, то через оба сечения пройдёт равный объём:

Это и есть уравнение неразрывности струи для несжимаемой жидкости.

22. Закон Бернулли.

Жидкость идеальна, движение стационарно.

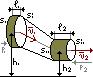
За малый промежуток времени жидкость перемещается от сечений S₁ и S₂ к сечениям S’₁ и S’₂.

По закону сохранения энергии изменение полной энергии идеальной несжимаемой жидкости равно работе внешних сил по перемещению массы жидкости:

,

где Е₁ и Е₂ – полные энергии жидкости массой m в местах сечений S₁ и S₂ соответственно.

С другой стороны А – это работа, совершаемая при перемещении всей жидкости, заключённой между сечениями S₁ и S₂, за рассматриваемый промежуток времени . Для переноса массы m от S₁ до S’₁ жидкость должна переместится на расстояние 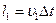и от S₂ до S’₂ на расстояние .

,

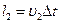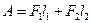где F₁=p₁S₁ и F₂=-p₂S₂.

Полные энергии Е₁ и Е₂ будут складываться из кинетической и потенциальной энергий массы жидкости:

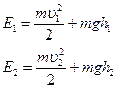
Получим:

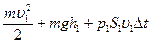
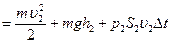
Учтя, что

разделим ур-е на :

,

т.к. сечения выбирались произвольно, то:

Это выражение и есть уравнение Бернулли – выражение закона сохранения энергии, применительно к установившемуся течению идеальной жидкости.

p – это статическое (избыточное) давление,

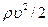- динамическое давление.

- гидростатическое давление.

Из ур-я Бернулли и ур-я неразрывности следует, что при течении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давление больше в более широких местах.

23. Формула Торричелли.

Рассмотрим два сечения (на уровне h₁ и h₂), напишем для них ур-е Бернулли:

,

Т.к. p₁=p₂=Атм., то:

из ур-я неразрывности следует, что

,

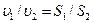Если S₁>>S₂, то 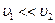, и членом 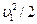можно пренебречь:

,

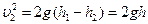
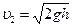это выражение и есть формула Торричелли.

24. Внутреннее трение (вязкость). Режимы течения.

Вязкость – св-во реальных жидкостей оказывать сопротивление перемещению одной части жидкости относительно другой.

Градиент скорости – величина показывает, как быстро меняется скорость при переходе от слоя к слою, в направлении перпендикулярном движению слоёв, т.о. сила трения:

,

где вязкость – коэффициент пропорциональности, зависящий от природы жидкости.

Режимы течения:

1) Ламинарное – течение, при котором каждый выделенный тонкий слой скользит относительно соседних, не перемешиваясь с ними.

Это течение наблюдается при низких скоростях её движения.

2) Турбулентное – течение, при котором вдоль потока происходит интенсивное вихреобразование, и перемешивание жидкости.

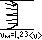
Частицы жидкостей приобретают составляющие скоростей, перпендикулярны течению, поэтому они могут переходить из одного слоя в другой. Из-за большого градиента скоростей у поверхности трубы происходит образование вихрей.

Вязкость жидкости – перенос импульса между контактирующими слоями.

-

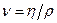кинематическая вязкость.

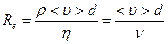
R_e – число Рейнольдса, характер движения завит от него:

R_e<=1000, то ламинарное

1000<=R_e<=2000, переход от ламинарного к турбулентному.

R_e=2300, то турбулентному

25. Метод Стокса.

Основан на измерении скорости медленно движущихся в жидкости небольших тел сферической формы.

На шарик, падающий в жидкости вертикально вниз, действуют 3 силы:

Сила тяжести: (плотность шарика)

Сила Архимеда: (плотность жидкости)

Сила сопротивления (Стокса): .

При равномерном движении шарика:

,

проекции:

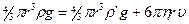
отсюда:

26. Метод Пуазейля.

Основан на ламинарном течении жидкости в тонком капилляре.

В жидкости мысленно выделим цилиндрический слой радиусом r и толщиной dr, сила внутреннего трения, действующая на боковую поверхность этого слоя равна:

,

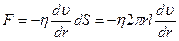где dS – боковая поверхность, есть (-), т.к. при возрастании радиуса скорость уменьшается.

Сила вязкости уравновешивается силой давления, действующей на основание:

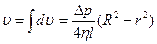
За время t из трубы вытечет жидкость объёмом:

.

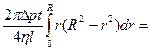
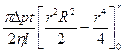
27. Поверхностное натяжение.

Для жидкости характерен ближний порядок расположения частиц, т.е. их упорядоченное расположение, повторяющееся на расстояниях, сравнимых с межатомными.

Радиус молекулярного действия (r=10^-9м) – С расстояния более этого радиуса силами межмолекулярного взаимодействия можно пренебречь.

Результирующие силы всех молекул поверхностного слоя оказывают на жидкость давление, называемое молекулярным, или внутренним.

У молекул на поверхности сущ-ет дополнительная П. энергия, называемая поверхностной энергией.

,

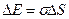где сигма – поверхностное натяжение.

,

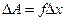где 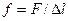- сила поверхностного натяжения, действующая на единицу длины контура поверхности жидкости.

,

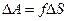эта работа совершается за счёт уменьшения поверхностной энергии, т.е.:

,

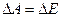
т.е. поверхностное натяжение равно силе поверхностного натяжения, действующей на единицу длины контура поверхности жидкости.

Поверхностно-активные – в-ва, влияющие на поверхностное натяжение жидкости.

(мыло - , соль/сахар - )

28. Смачивание и не смачивание.

Краевой угол – угол между касательными к поверхности жидкости и твёрдого тела.

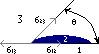
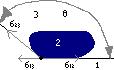
Условие равновесия капли является равенство нулю суммы проекций сил поверхностного натяжения на направление касательной к поверхности твёрдого тела:

;

,

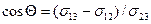из этого условия следует, что:

смачивание

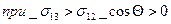
не смачивание

Условие равновесия жидкости:

.

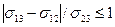Полное смачивание:

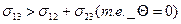
Полное не смачивание:

29. Давление под искривлённой поверхностью жидкости. Формула Лапласа.

Если поверхность жидкости не плоская, а искривленная, то она оказывает на жидкость избыточное (добавочное) давление, т.к. действуют силы поверхностного натяжения, для выпуклой поверхности положительно, а для вогнутой – отрицательно.

На каждый бесконечно малый элемент длины 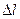контура действует сила поверхностного натяжения:

,

касательная к поверхности сферы.

Разложив на две составляющие , видим, что геометрическая сумма сил 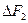равна нулю, т.е. равнодействующая сил поверхностного натяжения, действующих на вырезанный сегмент, направлена перпендикулярно плоскости сечения. И равна:

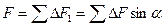
Это и есть формула избыточного (добавочного) давления для выпуклой поверхности.

Для вогнутой:

Эти две формулы являются частными случаями формулы Лапласа, определяющей избыточное давление для произвольной поверхности жидкости двоякой кривизны:

.

30. Капиллярные явления.

Капиллярность – явление изменения высоты жидкости в капиллярах.

Жидкость в капилляре поднимается или отпускается на такую высоту h, при которой давление столба жидкости (гидростатическое давление) уравновешивается избыточным давлением , т.е.:

, т.к. , то:

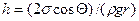
Дата добавления: 2015-04-24