Разность потенциалов

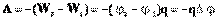
Напряжение — разность значений потенциала в начальной и конечной точках траектории.

Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля.

Разность потенциалов (напряжение) не зависит от выбора системы координат!

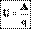
13. 1-ый закон Ньютона (Закон инерции). Существуют такие системы отсчёта, называемые инерциальными, относительно которых свободная материальная точка сохраняет величину и направление своей скорости неограниченно долго.

2-ой закон Ньютона (Закон движения). В инерциальной системе отсчета ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе. F ⃗ = ma ⃗

3-ий закон Ньютона. Материальные точки попарно действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению: F ⃗ 2→1=− F ⃗ 1→2.

14. Если мы имеем механическую систему, состоящую из многих тел, то, согласно 3-ему закону Ньютона, силы, действующие между этими телами, будут равны и проти­воположно направлены, т. е. геометрическая сумма внутренних сил равна нулю.

Рассмотрим механическую систему, состоящую из n тел, масса и скорость которых соответственно равны m ₁, m ₂,.... m_n, и v₁, v₂,..., v _n. Пусть 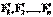— равнодейст­вующие внутренних сил, действующих на каждое из этих тел, a 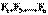— равно­действующие внешних сил. Запишем 2-ой закон Ньютона для каждого из n тел механической системы:

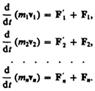
Складывая почленно эти уравнения, получаем

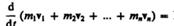
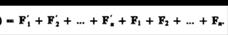
Но т.к. геометрическая сумма внутренних сил механической системы по 3-ему закону Ньютона равна нулю, то

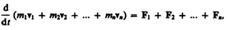
или

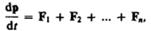
где 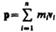— импульс системы. Таким образом, производная по времени от им­пульса механической системы равна геометрической сумме внешних сил, действующих на систему.

В случае отсутствия внешних сил (рассматриваем замкнутую систему)

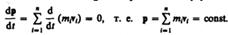
Последнее выражение и является законом сохранения импульса: импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени.

Закон сохранения импульса является следствием определенного свойства симмет­рии пространства — его однородности. Однородность пространства заключается в том, что при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства и законы движения не изменяются, иными словами, не зависят от выбора положения начала координат инерциальной системы отсчета.

15. Потенциал некоторой точки электростатического поля равен работе, совершаемой электрической силой при эвакуации единичного положительного заряда из этой точки в бесконечность.

Теперь вычислим потенциал поля, созданного системой точечных зарядов Q ₁, Q ₂, …, Q_N.

При перемещении заряда q из точки 1 в бесконечность электрическая сила совершит работу, равную алгебраической сумме работ сил, действующих на движущийся заряд со стороны зарядов Q ₁, Q ₂, …, Q_N (рис. 3.3.):

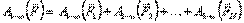
Рис. 3.3.

Согласно (3.12) работа каждой силы равна: 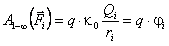. (3.13)

Здесь 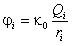— потенциал поля, создаваемого в точке 1 зарядом Q_i.

Таким образом, суммарная работа равна:

,

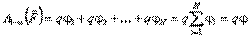где .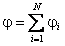

Потенциал поля, созданного системой точечных зарядов, равен алгебраической сумме потенциалов, создаваемых в рассматриваемой точке каждым из зарядов в отдельности:

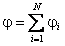. (3.14)

Результат (3.14) известен как «принцип суперпозиции для потенциала». Это очень важный вывод, позволяющий использовать понятие потенциала не только для характеристики полей точечных зарядов, но и для любых произвольных электростатических полей.

16. Перенесем положительный заряд Q2 из бесконечности на расстояние R от положительного заряда Q1. Если заряды разноименны, то направление переноса сменим на противоположное, - лишь бы работа по переносу одного заряда производилась против поля другого заряда и тем самым превратилась в потенциальную энергию образованной системы зарядов.

В результате произведенной работы заряд Q2 оказался в точке с потенциалом 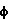1 поля заряда Q1, и его потенциальная энергия равна:

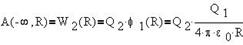
Точно такую же работу надо было бы совершить при переносе заряда Q1 в поле заряда Q2. Иными словами, в системе отсчета, связанной с зарядом Q2 эта же работа равна:

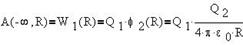
Энергия системы зарядов оказывается равной полусумме потенциальных энергий обоих зарядов:

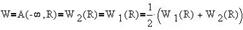
В общем случае n точечных зарядов каждый i-й заряд обладает потенциальной энергией в суммарном поле остальных зарядов, и полная энергия всей системы есть полусумма потенциальных энергий всех зарядов:

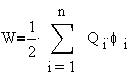
Здесь 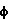i - суммарный потенциал поля зарядов, взаимодействующих с Q i.

17. Работа постоянной силы ее свойства. Для характеристики эффективности силового воздействия на тело используется величина, называемая механической работой. Пусть под действием постоянной силы F тело переместилось из положения 1 в положение 2 вдоль прямой линии.

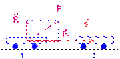Смещение тела охарактеризуем вектором S. Работой силы F на перемещении S называется скалярная величина, определяемая равенством: A = | F |·| S |·cosa = (F · S)

Дата добавления: 2015-04-24