
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кратность вырождения уровней энергий. Символика обозначения квантовых состояний
|
|
|
|
Вырождение энергетических уровней -существование двух или более стационарных состояний квантовой системы (атома, молекулы) с одинаковыми значениями энергии. Система, полная энергия которой определяется заданием оператора Я (гамильтониана), может иметь т стационарных состояний, для которых уравнение Шредингера Hφi = Eφi определяет соответствующие волновые функции φi (i = 1, 2,..., т) и одно значение энергии Е, одинаковое для всех т состояний. Энергетический уровень с энергией Е при m ≠ 1 называется вырожденным, число т различных независимых волновых функций - кратностью вырождения уровня. О состояниях с волновыми функциями φi говорят как о состояниях, вырожденных по энергии, или вырожденных состояниях. Если одному значению энергии отвечает одно состояние, т.е. m=1, уровень наз. невырожденным.
Для обозначения квантовых состояний с заданным значением орбитального квантового числа l используют следующие спектроскопические символы:
l 0 1 2 3
Обозначение s p q f
подоболочки
Для обозначения квантовых состояний с заданным значением главного квантового числа n используют следующие спектроскопические символы:
n 1 2 3 4
Обозначение K L M N
оболочки
(23/24/25). Магнитные свойства атома. Спин электрона. Орбитальные и спиновые характеристики электрона в атоме. Опыт Штерна – Герлаха
В соответствии с классической электродинамикой, движущийся по замкнутой траектории электрон, будучи подобен току, возбуждает в окружающем пространстве магнитное поле, и имеет магнитный момент, величина которого определяется по формуле 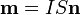 , где s– площадь, охватываемая орбитой электрона;n– единичный нормальный к s вектор;
, где s– площадь, охватываемая орбитой электрона;n– единичный нормальный к s вектор;
I – сила тока, причем ток направлен противоположно направлению скорости электрона;
Так как 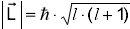 то Pm может принимать значения:
то Pm может принимать значения:
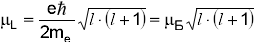 где магнетон Бора.
где магнетон Бора. 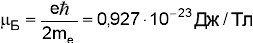 .
.
Это значение магнитного момента, которое имел бы атом водорода, если бы электрон был классической частицей и вращался по первой боровской орбите. Таким образом, магнитный момент, как физическая величина квантуется подобно механическому моменту и может принимать лишь значения кратные магнетону Бора.
Спин - собственный момент импульса (или магнитный момент) элементарных частиц, имеющий квантовую природу и не связанный с перемещением частицы как целого.
Отношение величины магнитного момента к величине спина называется гиромагнитным отношением, и, в отличие от орбитального углового момента, оно не равно магнетону (μ0): 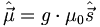 Введённый здесь множитель g называется g-фактором частицы;
Введённый здесь множитель g называется g-фактором частицы;
Спин электрона равен 1/2.
Орбитальное квантовое число l определяет значение орбитального момента количества движения электрона на данной орбитали. Допустимые значения: 0, 1, 2, 3,...n-1.
Орбитальное квантовое число определяет форму поверхности максимальной вероятности нахождения электрона и ее симметрию.
Спиновое квантовое число ms. Каждый электрон также характеризуется собственным механическим моментом движения, который получил название speen. Спиновое квантовое число ms имеет только два значения +1/2 и -1/2, которые связаны с его направлением.
Наличие у атомов магнитных свойств и явление пространственного квантования (квантование проекции момента импульса) были обнаружены в опытах Штерна и Герлаха (1921-1923 гг.) еще до появления квантовой механики.Как известно, на магнитный момент в неоднородном магнитном поле действует сила, определяемая соотношением:
F= μz дН/дZ
которая отклоняет его от первоначального направления движения. Если проекция магнитного момента атома могла бы изменяться непрерывно, то на пластинке П наблюдалась бы размытая широкая полоса. Однако в Ш.— Г. о. было обнаружено расщепление пучка атомов на 2 компоненты, симметрично смещенные относительно первичного направления распространения на величину Δ — на пластинке появлялись две узкие полосы. Это указывало на то, что проекция магнитного момента атома μz на направление поля Н принимает только два отличающиеся знаком значения ±μo, т. е. μo ориентируется вдоль Н и в противоположном направлении. Величина магнитного момента атома μо, измеренная в опыте по смещению Δ, оказалась равной Бора магнетону.
(26). Символика обозначений квантовых состояний. Понятие о вырождении. Принцип Паули. Периодическая система Менделеева
Для обозначения квантовых состояний с заданным значением орбитального квантового числа l используют следующие спектроскопические символы:
l 0 1 2 3
Обозначение s p q f
подоболочки
Для обозначения квантовых состояний с заданным значением главного квантового числа n используют следующие спектроскопические символы:
n 1 2 3 4
Обозначение K L M N
оболочки
Энергетический уровень квантовой системы называется вырожденным, если содержит более одного состояния. Говоря математически, соответствующее значение энергии является кратным собственным значением оператора гамильтониана.
Количество независимых таких состояний (т.е. кратность собственного значения) называется кратностью вырождения.
Для многоэлектронных атомов выполняется принцип запрета Паули: в одном и том же атоме не может быть двух электронов, обладающих одинаковым набором четырех квантовых чисел.
Периодическая система химических элементов (таблица Менделеева) — классификация химических элементов, устанавливающая зависимость различных свойств элементов от числа протонов в атомном ядре. Система является графическим выражением периодического закона, установленного русским химиком Д. И. Менделеевым в 1869 году.
В современном варианте системы предполагается сведение элементов в двухмерную таблицу, в которой каждый столбец (число столбцов составляет 8) определяет основные физико-химические свойства, а строки представляют собой периоды, в определённой мере подобные друг другу.
Тождественные (иначе неразличимые) частицы — это частицы, которые принципиально не могут быть распознаны и отличены одна от другой, то есть подчиняются Принципу тождественности одинаковых частиц. К таким частицам относятся: элементарные частицы(электроны, нейтроны и т. д.) а также составные микрочастицы, такие как атомы и молекулы. Существует два больших класса тождественных частиц: бозоны и фермионы.
Бозо́н (от фамилии физика Бозе) — частица с целым значением спина. Термин был предложен физиком Полем Дираком[1]. Бозоны, в отличие от фермионов, подчиняются статистике Бозе — Эйнштейна, которая допускает, чтобы в одном квантовом состоянии могло находиться неограниченное количество одинаковых частиц. Системы из многих бозонов описываются симметричными относительно перестановок частиц волновыми функциями. Различают элементарные бозоны и составные.
Элементарные бозоны являются квантами калибровочных полей, при помощи которых осуществляется взаимодействие элементарных фермионов (лептонов и кварков) в Стандартной модели. К таким калибровочным бозонам относят:
· фотон (электромагнитное взаимодействие),
· глюон (сильное взаимодействие)
· W± и Z-бозоны (слабое взаимодействие).
Кроме этого, к элементарным бозонам относят бозон Хиггса, ответственный за механизм появления масс в электрослабой теории, и не обнаруженный до настоящего времени гравитон (гравитационное взаимодействие).
Все элементарные бозоны, за исключением W±-бозонов, являются незаряженными. W+ и W− бозоны по отношению друг к другу выступают как античастицы. Калибровочные бозоны (фотон, глюон, W± и Z-бозоны) имеют единичный спин. Гипотетический гравитон — спин 2, ибозон Хиггса — спин 0.
К составным бозонам относят многочисленные двухкварковые связанные состояния, называемые мезонами. Как и у любых бозонов, спин мезонов является целочисленным, и его значение, в принципе, не ограничено (0,1,2,3,…). Другими примерами бозонов являются ядра, содержащие чётное количество нуклонов (протонов и нейтронов).
Фермио́н — частица (или квазичастица) с полуцелым значением спина. Своё название получили в честь физика Энрико Ферми.
Примеры фермионов: кварки (они образуют протоны и нейтроны, которые также являются фермионами), лептоны (электроны, мюоны, тау-лептоны, нейтрино), дырки (квазичастицы в полупроводнике)[1].
Фермионы подчиняются статистике Ферми — Дирака: в одном квантовом состоянии может находиться не более одной частицы (принцип Паули). Принцип запрета Паули ответственен за устойчивость электронных оболочек атомов, делая возможным существование сложных химических элементов. Он также позволяет существовать вырожденной материи под действием высоких давлений (нейтронные звёзды). Волновая функция системы одинаковых фермионов антисимметрична относительно перестановки двух любых фермионов. Квантовая система, состоящая из нечётного числа фермионов, сама является фермионом (например, ядро с нечётным массовым числом A; атом или ион с нечётной суммой A и числа электронов).
27. Если тождественные частицы имеют одинаковые квантовые числа, то их волновая функция симметрична относительно перестановки частиц. Отсюда следует, что два одинаковых фермиона, входящих в одну систему, не могут находиться в одинаковых состояниях, т.к. для фермионов волновая функция должна быть антисимметричной. Обобщая опытные данные, В. Паули сформировал принциписключения, согласно которому системы фермионов встречаются в природе только в состояниях, описываемых антисимметричными волновыми функциями (квантово-механическая формулировка принципа Паули).
| Паули Вольфганг (1900–1958) – физик-теоретик. Работы относятся ко многим разделам современной теоретической физики, в развитии которых он принимал непосредственное участие, в частности квантовой механике, квантовой электродинамике, теории относительности, квантовой теории поля, ядерной физике, физике элементарных частиц. |
Из этого положения вытекает более простая формулировка принципа Паули, которая и была введена им в квантовую теорию (1925 г.) еще до построения квантовой механики: в системе одинаковых фермионовлюбые два из них не могут одновременнонаходиться в одном и том же состоянии. Отметим, что число одинаковых бозонов, находящихся в одном и том же состоянии, не лимитируется.
Напомним, что состояние электрона в атоме однозначно определяется набором четырех квантовых чисел:
· главного n;
· орбитального l, обычно эти состояния обозначают 1 s, 2 d, 3 f;
· магнитного ();
· магнитного спинового ().
Распределение электронов в атоме происходит по принципу Паули, который может быть сформулирован для атома в простейшем виде: в одном и том же атоме не может быть более одного электрона с одинаковым набором четырех квантовых чисел: n, l,,:
Z (n, l,,) = 0 или 1,
где Z (n, l,,) - число электронов, находящихся в квантовом состоянии, описываемых набором четырех квантовых чисел: n, l,,. Таким образом, принцип Паули утверждает, что два электрона, связанные в одном и том же атоме различаются значениями, по крайней мере, одного квантового числа.
Максимальное число электронов, находящихся в состояниях, описываемых набором трех квантовых чисел n, l и m, и отличающихся только ориентацией спинов электронов равно:
| , | (8.2.1) |
ибо спиновое квантовое число может принимать лишь два значения 1/2 и –1/2.
Максимальное число электронов, находящихся в состояниях, определяемых двумя квантовыми числами n и l:
| . | (8.2.2) |
При этом вектор орбитального момента импульса электрона может принимать в пространстве (2 l + 1) различных ориентаций (рис. 8.1).
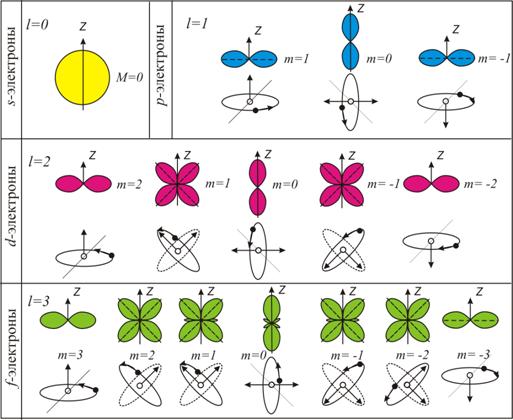
Рис. 8.1
Максимальное число электронов, находящихся в состояниях, определяемых значением главного квантового числа n, равно:
| . | (8.2.3) |
Совокупность электронов в многоэлектронном атоме, имеющих одно и то же главное квантовое число n, называется электронной оболочкой или слоем.
В каждой из оболочек электроны распределяются по подоболочкам, соответствующим данному l.
Область пространства, в которой высока вероятность обнаружить электрон, называют подоболочкой или орбиталью. Вид основных типов орбиталей показан на рис. 8.1.
Поскольку орбитальное квантовое число принимает значения от 0 до, число подоболочек равно порядковому номеру n оболочки. Количество электронов в подоболочке определяется магнитным и магнитным спиновым квантовыми числами: максимальное число электронов в подоболочке с данным l равно 2(2 l + 1). Обозначения оболочек, а также распределение электронов по оболочкам и подоболочкам приведено в табл. 1.
Таблица 1
| Главное квантовое число n | |||||||||||||||
| Символ оболочки | K | L | M | N | O | ||||||||||
| Максимальное число электроновв оболочке | |||||||||||||||
| Орбитальное квантовое число l | |||||||||||||||
| Символ подоболочки | 1s | 2s | 2p | 3s | 3p | 3d | 4s | 4p | 4d | 4f | 5s | 5p | 5d | 5f | 5g |
| Максимальное число электронов в подоболочке |
| 28.Характеристическое рентгеновское излучение | |
Когда энергия бомбардирующих анод электронов становится достаточной для вырывания электронов из внутренних оболочек атома, на фоне тормозного излучения появляются резкие линии характеристического излучения. Частоты этих линий зависят от природы вещества анода, поэтому их и назвали характеристическими.
Состояние атома с вакансией во внутренней оболочке неустойчиво. Электрон одной из внешних оболочек может заполнить эту вакансию, и атом при этом испускает избыток энергии в виде фотона характеристического излучения:
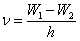 .
Все переходы на k -оболочку образуют K- серию, соответственно, на l- и m- оболочки – L- и M- серии (рис. 2.8). .
Все переходы на k -оболочку образуют K- серию, соответственно, на l- и m- оболочки – L- и M- серии (рис. 2.8).
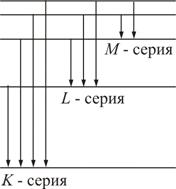 Рис. 2.8
Английский физик Генри Мозли в 1913 году установил закон, названный его именем, связывающий частоты линий рентгеновского спектра с атомным номером испускающего их элемента Z: Рис. 2.8
Английский физик Генри Мозли в 1913 году установил закон, названный его именем, связывающий частоты линий рентгеновского спектра с атомным номером испускающего их элемента Z:
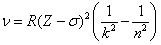 , где k = 3, 4, 5…; n = k +1, k +2, k +3….
Здесь, постоянная Ридберга; σ – постоянная, учитывающая экранирующую роль окружающих ядро электронов. Чем дальше электрон от ядра, тем σ больше. , где k = 3, 4, 5…; n = k +1, k +2, k +3….
Здесь, постоянная Ридберга; σ – постоянная, учитывающая экранирующую роль окружающих ядро электронов. Чем дальше электрон от ядра, тем σ больше.
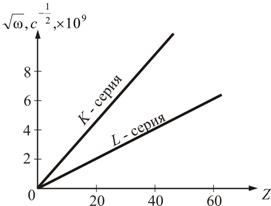 Рис. 2.9
На рис. 2.9 показана графическая зависимость закона.
Закон Мозли позволил по измерению длин волн λ рентгеновских лучей точно установить атомный номер элемента. Он сыграл большую роль при размещение элементов в таблице Менделеева.
Рентгеновское излучение. Тормозное и характеристическое излучение. Закон Мозли.
Рентгеновское излучение — электромагнитные волны, энергия фотонов которых лежит на энергетической шкале между ультрафиолетовым излучением и гамма-излучением, что соответствует длинам волн от 10−4 до 10² Å (от 10−14 до 10−8 м).
Тормозное излучение возникает при торможении электронов антикатодом рентгеновской трубки. Оно разлагается в сплошной спектр, имеющий резкую границу со стороны малых длин волн. Положение этой границы определяется энергией падающих на вещество электронов и не зависит от природы вещества.
Характеристическиерентгеновские лучи образуются при выбивании электрона одного из внутренних слоёв атома с последующим переходом на освободившуюся орбиту электрона с какого-либо внешнего слоя. Они обладают линейчатым спектром, аналогичным оптическим спектрам газов.
Закон Мозли - закон, связывающий частоту спектральных линий характеристического рентгеновского излучения химического элемента с его порядковым номером. Согласно Закону Мозли, корень квадратный из частоты n спектральной линии характеристического излучения элемента есть линейная функция его порядкового номера Z:
Рис. 2.9
На рис. 2.9 показана графическая зависимость закона.
Закон Мозли позволил по измерению длин волн λ рентгеновских лучей точно установить атомный номер элемента. Он сыграл большую роль при размещение элементов в таблице Менделеева.
Рентгеновское излучение. Тормозное и характеристическое излучение. Закон Мозли.
Рентгеновское излучение — электромагнитные волны, энергия фотонов которых лежит на энергетической шкале между ультрафиолетовым излучением и гамма-излучением, что соответствует длинам волн от 10−4 до 10² Å (от 10−14 до 10−8 м).
Тормозное излучение возникает при торможении электронов антикатодом рентгеновской трубки. Оно разлагается в сплошной спектр, имеющий резкую границу со стороны малых длин волн. Положение этой границы определяется энергией падающих на вещество электронов и не зависит от природы вещества.
Характеристическиерентгеновские лучи образуются при выбивании электрона одного из внутренних слоёв атома с последующим переходом на освободившуюся орбиту электрона с какого-либо внешнего слоя. Они обладают линейчатым спектром, аналогичным оптическим спектрам газов.
Закон Мозли - закон, связывающий частоту спектральных линий характеристического рентгеновского излучения химического элемента с его порядковым номером. Согласно Закону Мозли, корень квадратный из частоты n спектральной линии характеристического излучения элемента есть линейная функция его порядкового номера Z: 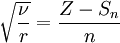 , где R — постоянная Ридберга, Sn — постоянная экранирования, n — главное квантовое число. , где R — постоянная Ридберга, Sn — постоянная экранирования, n — главное квантовое число.
|
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 11143; Нарушение авторских прав?; Мы поможем в написании вашей работы!